苏科版八年级上册2.5 等腰三角形的轴对称性课前预习ppt课件

这是一份苏科版八年级上册2.5 等腰三角形的轴对称性课前预习ppt课件，共9页。PPT课件主要包含了你还有其他发现吗，求证MN⊥BD等内容，欢迎下载使用。

【探究1】你能用折纸的方法将一个直角三角形分成 两个等腰三角形吗？
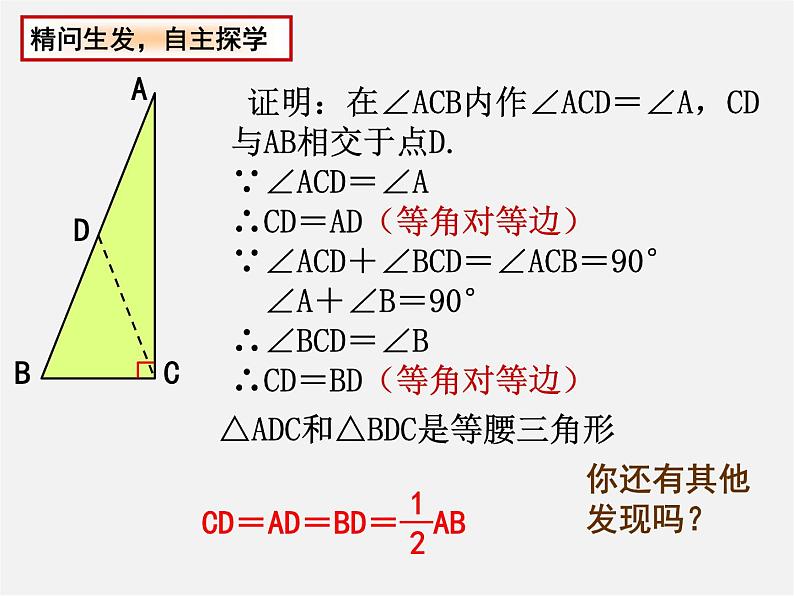
图(3)中的△ADC和△BDC是等腰三角形吗？为什么？
证明：在∠ACB内作∠ACD＝∠A，CD与AB相交于点D.∵∠ACD＝∠A∴CD＝AD（等角对等边）∵∠ACD＋∠BCD＝∠ACB＝90° ∠A＋∠B＝90°∴∠BCD＝∠B∴CD＝BD（等角对等边）
△ADC和△BDC是等腰三角形
在Rt△ABC中，∵∠ACB＝90°，D是AB的中点 （或CD＝AD＝BD）
（直角三角形斜边上的中线等于斜边的一半）
定理：直角三角形斜边上的中线 等于斜边的一半
（1）Rt△ABC中，如果斜边AB＝4cm，那么斜边上的中线CD＝______cm．
（2）如图，在Rt△ABC中，CD是斜边AB上的中线，DE⊥AC ，垂足为E． ①如果CD＝2.4cm，那么AB＝_____cm． ②写出图中相等的线段和角．
（3）在Rt△ABC中，∠ACB＝90°，CA＝CB，如果斜边AB＝5cm，那么AB边上的高CD＝______cm．
【例1】已知：如图，Rt△ABC，∠ACB＝90°，如果∠B＝30°，那么直角边AC、斜边AB之间有怎样的数量关系？试证明你的结论．
A B
定理：在直角三角形中，如果有一个锐角等于30°， 那么这个锐角所对的直角边等于斜边的一半．
【例2】已知：如图，点C为线段AB的中点，∠AMB＝∠ANB＝90°．CM与CN是否相等？为什么？
A B
【变式】已知：如图，点C为线段AB的中点，∠AMB＝∠ANB＝90°．若点P为线段MN的中点，判断CP与MN的位置关系，并说明理由．
【练习】已知：如图，在四边形ABCD中，∠ABC＝∠ADC＝90°，M、N分别是AC、BD的中点． 求证：（1）MD＝MB；（2）MN⊥BD