数学九年级上册21.1 圆的有关概念试讲课课件ppt

这是一份数学九年级上册21.1 圆的有关概念试讲课课件ppt，共41页。PPT课件主要包含了点与圆的位置关系，想一想，同心圆等内容，欢迎下载使用。

一、创设情境 引入新课
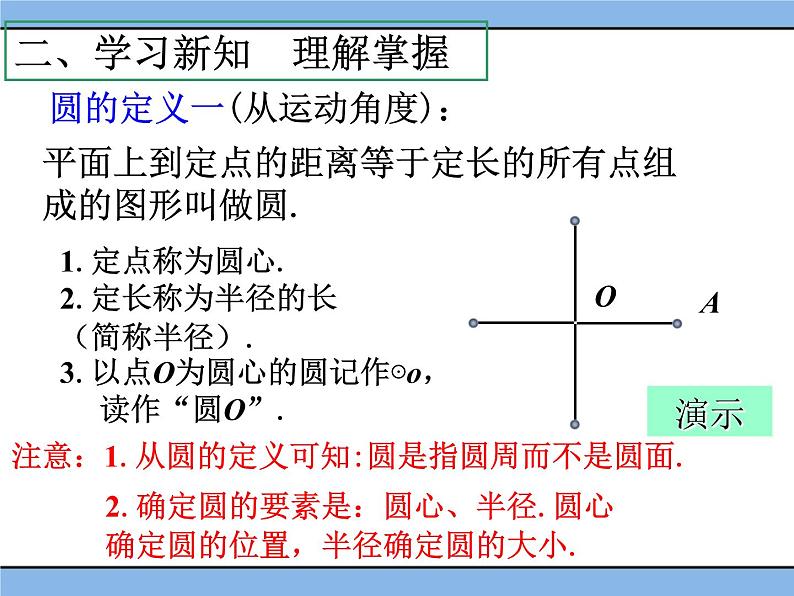
平面上到定点的距离等于定长的所有点组成的图形叫做圆.
注意：1.从圆的定义可知:圆是指圆周而不是圆面.
2.确定圆的要素是：圆心、半径.圆心确定圆的位置，半径确定圆的大小.
1.定点称为圆心.2.定长称为半径的长（简称半径）.3.以点O为圆心的圆记作⊙，读作“圆O”.
圆的定义一(从运动角度)：
二、学习新知 理解掌握
试根据圆的定义填空：1、圆上各点到 的距离都等 于 .2、到定点的距离等于定长的点都在 .
圆是到定点的距离等于定长的点的集合.
圆的内部:可以看作是到圆心的距离小于半径的点的集合.圆的外部:可以看作是到圆心的距离大于半径的点的集合.
圆的定义二(从集合角度)：
提问: 如果一个点到圆心距离小于半径， 那么这个点在哪里呢? 大于圆的半径呢? 反过来呢?
如图，设⊙O的半径为r，A点在圆内，B点在圆上，C点在圆外，那么
OA＜r， OB＝r， OC＞r．
点的位置可以确定该点到圆心的距离与半径的关系，反过来，已知点到圆心的距离与半径的关系可以确定该点到圆的位置关系.
如图所示， ⊙O是一个半径为r的圆.在圆内、圆外、圆上分别取一点，点到圆心的距离为d，请用r与d的大小来刻画它们的位置特征.
点与圆位置关系有三种:
点在圆外、点在圆上、点在圆内
点在圆外，即d ＞ r;点在圆上，即d ＝ r;点在圆外，即d ＜ r.
车轮为什么做成圆形?
三、学以致用 应用新知
车轮做成三角形、正方形可以吗？
如图，A，B表示车轮边缘上的两点，点O表示车轮的轴心，A，O之间的距离与B，O之间的距离有什么关系？
C表示车轮边缘上的任意一点.要使车轮能够平稳地滚动，C，O之间的距离与A，O之间的距离应满足什么关系？
车轮边缘上任意两点到轴心的距离都相等， 任意一点到轴心的距离是一个定值.
为了使投圈游戏公平，现在有一条3米长的绳子， 你准备怎么办?
四、学以致用 应用新知
五、例题分析 运用新知
例1 在△ABC中，∠C=900，AC=4，AB=5，以点C为圆心，以r为半径作圆，按下列条件分别判断A，B两点和⊙C的位置关系：
（1） r=2.4 （2） r=4
解：∵∠C=900，AC=4，AB=5，
（1） r=2.4时，
∵BC=3＞r ，AC=4＞r ，
∴A，B两点都在⊙C外.
∵BC=3＜r ，AC=4＝r ，
∴点B在⊙C内，点A在⊙C上.
例2 已知四边形ABCD为矩形.试判断A，B，C，D四个点是否在同一个圆上，并说明理由.
解： A，B，C，D四个点在同一个圆上.
如图21-3，连接AC，BD，AC与BD相交于O.
∵四边形ABCD为矩形.
∴OA=OC=OB=OD.
∴A，B，C，D四个点在以点O为圆心，OA为半径的圆上.
六、当堂检测 巩固新知
（以点A为圆心，2厘米长为半径的圆）
（以点A为圆心，2厘米长为半径 的圆的内部）
（分别以点A 、B为圆心，2厘米长为半径的⊙ A和⊙B的交点）
（分别以点A、 B为圆心，2厘米长为半径的⊙ A的内部与⊙B的内部的公共部分）
1、从运动和集合的观点理解圆的定义：
3、证明几个点在同一个圆上的方法.
要证明几个点在同一个圆上，只要证明这几个点与一个定点的距离相等.
2、点与圆的位置关系：
七、课堂小结 知识提升
等圆：圆心不同半径相同
同心圆：圆心相同半径不同
八、学习新知 理解掌握
认识弧、弦、直径这些与圆有关的概念
如图， 弦AB，弦CD
圆上任意两点间的部分叫做圆弧，简称弧.
连接圆上任意两点的线段叫做弦.
直径：经过圆心的弦叫做直径.
半圆：圆的任意一条直径的两个端点分圆 成两 条弧，每条弧叫做半圆.
3.等弧：在同圆或等圆中，能够互相重合的弧 叫做等弧.
如图是某市的摩天轮的示意图. 点O是圆心，半径r为15m，点A，B是圆上的两点，圆心角∠AOB=120°. 你能想办法求出 的长度吗？说说你的理由.
我们知道圆周长的计算公式为C=2πr，其中r是圆的半径，即360°的圆心角所对的弧长就是圆周长C.
例3 已知圆O的半径为30cm，求40°的圆心角所对的弧长(精确到0.1cm)
如图所示，一个边长为10cm的等边三角形木板ABC在水平桌面上绕顶点C按顺时针方向旋转到△A′B′C的位置，求顶点A从开始到结束所经过的路程为多少.
九、学以致用 应用新知
∵ 等边三角形ABC的边长为10cm，
圆的一条弧和经过这条弧的端点的两条半径所围成的图形叫作扇形.
我们可以发现，扇形面积与组成扇形的圆心角的大小有关，在同一个圆中，圆心角越大，扇形面积也越大.
如何求半径为r，圆心角为n°的扇形的面积呢？
例4 如图，圆O的半径为1.5cm，圆心角∠AOB=58°，求扇形OAB的面积.(精确0.1cm2).
解 因为r=1.5cm，n=58，
所以扇形OAB的面积为
解 设∠AOB=n°，
解得n=135°，即圆心角∠COD=135°.
∵⊙O切BC、AC于点D、E，
∴OD⊥BC，OE⊥AC.
∴四边形OECD为矩形，∠EOD=90°， OE=OD.