



初中数学北京课改版九年级上册21.3 圆的对称性获奖ppt课件
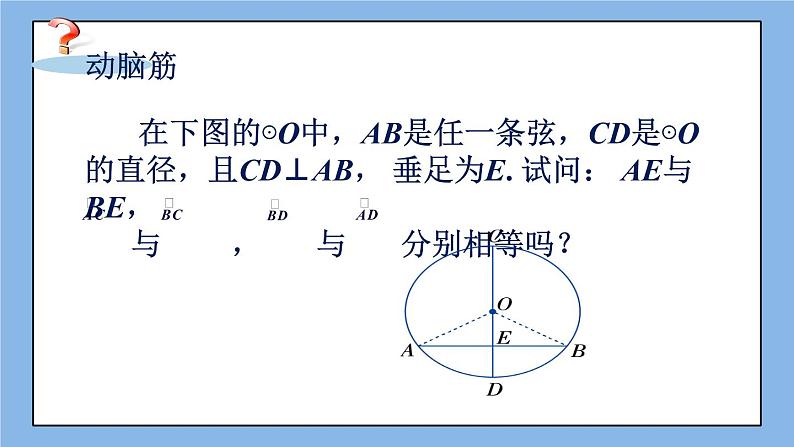
展开在下图的⊙O中,AB是任一条弦,CD是⊙O的直径,且CD⊥AB, 垂足为E. 试问: AE与BE, 与 , 与 分别相等吗?
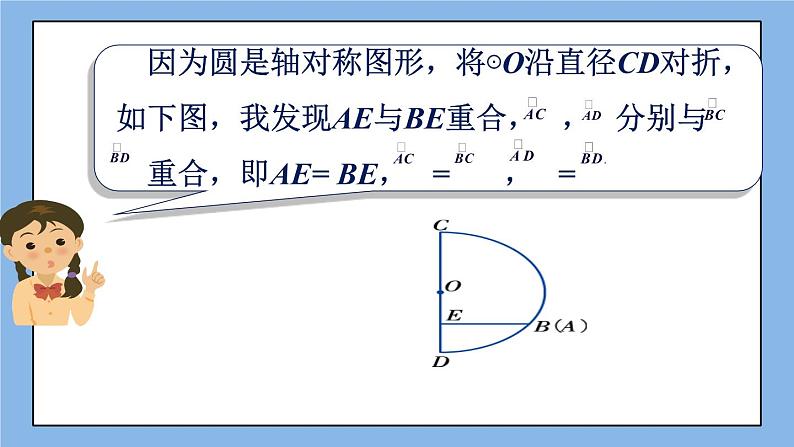
从而∠AOC =∠BOC.
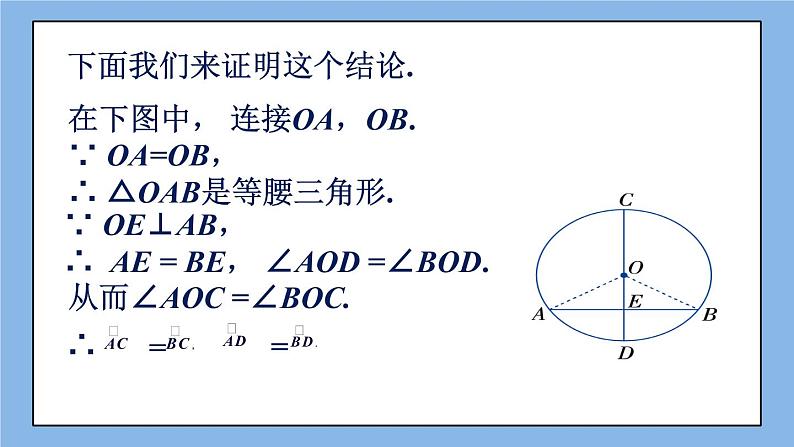
下面我们来证明这个结论.
在下图中, 连接OA,OB.
∵ OA=OB,∴ △OAB是等腰三角形.
∵ OE⊥AB,∴ AE = BE, ∠AOD =∠BOD.
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
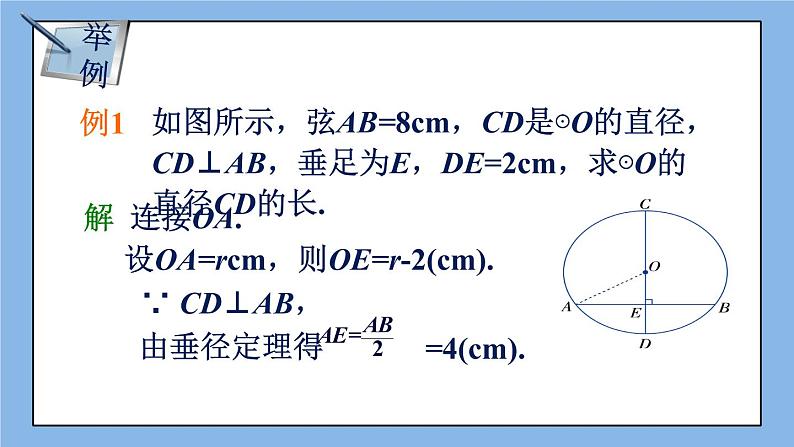
设OA=rcm,则OE=r-2(cm).
∴ CD = 2r = 10 (cm).
证明 作直径EF⊥AB,
又 AB∥CD,EF⊥AB,
∵AD=37.4,DC= 7.2,
OD=OC- DC=R-7.2.
在Rt△OAD中,由勾股定理,得: OA2 =AD2+OD2.
答:桥拱所在圆的半径约为27.9m.
即R2 =18.72+(R-7.2)2.
1、如果圆的两条弦互相平行,那么这两条弦所夹的弧相等吗?为什么?
提示: 这两条弦在圆中位置有两种情况。
(1)两条弦在圆心的同侧
(2)两条弦在圆心的两侧
2、如图,一 条公路的转弯处是一段弧(即图中 ,点O是 所在圆的圆心).其中CD = 600m,E为 上一点,且OE⊥CD,垂足为F,EF = 90m.求这段弯路的半径.
则:OF = (R-90)m,∵OE⊥CD,∴CF = CD= ×600 = 300(m),在Rt△OCF中,由勾股定理得:OC2 = CF2+OF2,∴R2 = 3002+(R-90)2解得:R = 545,∴这段弯路的半径为545m.
解:连接OC,设弯路的半径为Rm,
问题1:前面我们已经认识了圆,你还记得确定圆的两个元素吗?
问题2:你还记得知道圆中的哪些概念吗?
1.弧:圆上_________________叫做圆弧,简称弧.
3._______________叫做等圆,_____________________________叫做等弧.
在同圆或等圆中,能够重合的两条弧
2.弦:连接_________________叫做弦,经过圆心的弦叫做______.
(1)圆是轴对称图形吗?如果是,它的对称轴是什么?你能找到多少条对称轴?
(2)同伴交流:你是用什么方法解决上述问题?
请同学们用自己准备好的圆形纸张折叠:看折痕经不经过圆心?
结论:我们通过折叠的方法得到圆是轴对称图 形,经过圆心的一条直线是圆的对称轴 ,圆的对称轴有无数条.
探究二:圆的中心对称性
一个圆绕着它的圆心旋转任意一个角度,还能与原来的图形重合吗?
结论1:一个圆绕着它的圆心旋转任意一个角 度,都能与原来的图形重合,我们把 圆的这个特性称之为圆的旋转不变性.结论2:圆是中心对称图形,对称中心为圆心.
探究三:圆心角、弧、弦之间的关系
在等圆⊙O和⊙O′中,分别作相等的圆心角∠AOB和∠A ′OB ′(如图3-8),将两圆重叠,并固定圆心,然后把其中的一个圆旋转一个角度,得OA与OA′重合.
你能发现哪些等量关系?说一说你的理由?
小红认为 = ,AB= .她是这样想的:∵半径OA重合,∠AOB= ,∴半径OB与 重合,∵点A与点 重合,点B与点B′重合,∴ 与 重合,弦AB与弦 重合.∴ = ,AB= .
结论:在同圆或等圆中,相等的圆心角所对的 弧相等,所对的弦相等.
在同圆或等圆中,如果两个圆心角所对的弧相等,那么它们所对的弦相等吗?这两个圆心角相等吗?你是怎么想的?
结论:在同圆或等圆中,如果两个圆心角、两条 弧、两条弦中有一组量相等,那么它们所 对应的其余各组量都分别相等.
例4已知:A,B是⊙O上的两点,∠AOB=120°,C是 的中点.试判断四边形AOBC的形状,并说明理由.
解:四边形AOBC为菱形.
∴四边形AOBC为菱形.
如图21-26,连接OC.
∵∠AOB=120°,
又∵OA=OC=OB ,
∴△AOC,△BOC均为等边三角形.
∴AC=AO=BO =BC.
1.日常生活中的许多图案或现象都与圆的对称性有关,试举几例.
2.利用一个圆及其若干条弦分别设计出符合下列 条件的图案: (1)是轴对称图形但不是中心对称图形; (2)是中心对称图形但不是轴对称图形; (3)既是轴对称图形又是中心对称图形.
如图,在△ABC中,∠C=90°,∠B=25°,以点C为圆心,AC为半径的圆交AB于点D,求 所对的圆心角的度数.
解:连接CD,∵ ∠C = 90°,∠B = 25°,∴∠A = 90°-25°=65°,∵CA = CD,∴∠A = ∠CDA = 65°,∴∠ACD=180°-2×65°=50°,∴ 所对的圆心角的度数为50°.
初中数学北京课改版九年级上册21.3 圆的对称性集体备课ppt课件: 这是一份初中数学北京课改版九年级上册21.3 圆的对称性集体备课ppt课件,
北京课改版九年级上册21.3 圆的对称性课文ppt课件: 这是一份北京课改版九年级上册21.3 圆的对称性课文ppt课件,
北京课改版九年级上册21.3 圆的对称性评课课件ppt: 这是一份北京课改版九年级上册21.3 圆的对称性评课课件ppt,













