数学2.1 有理数教学课件ppt

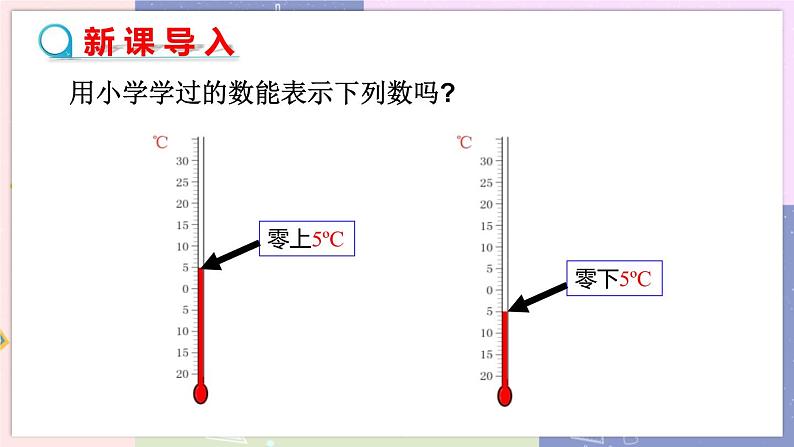
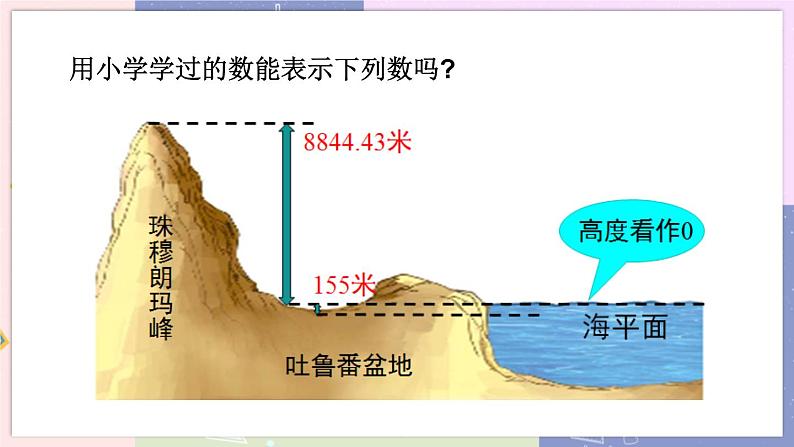
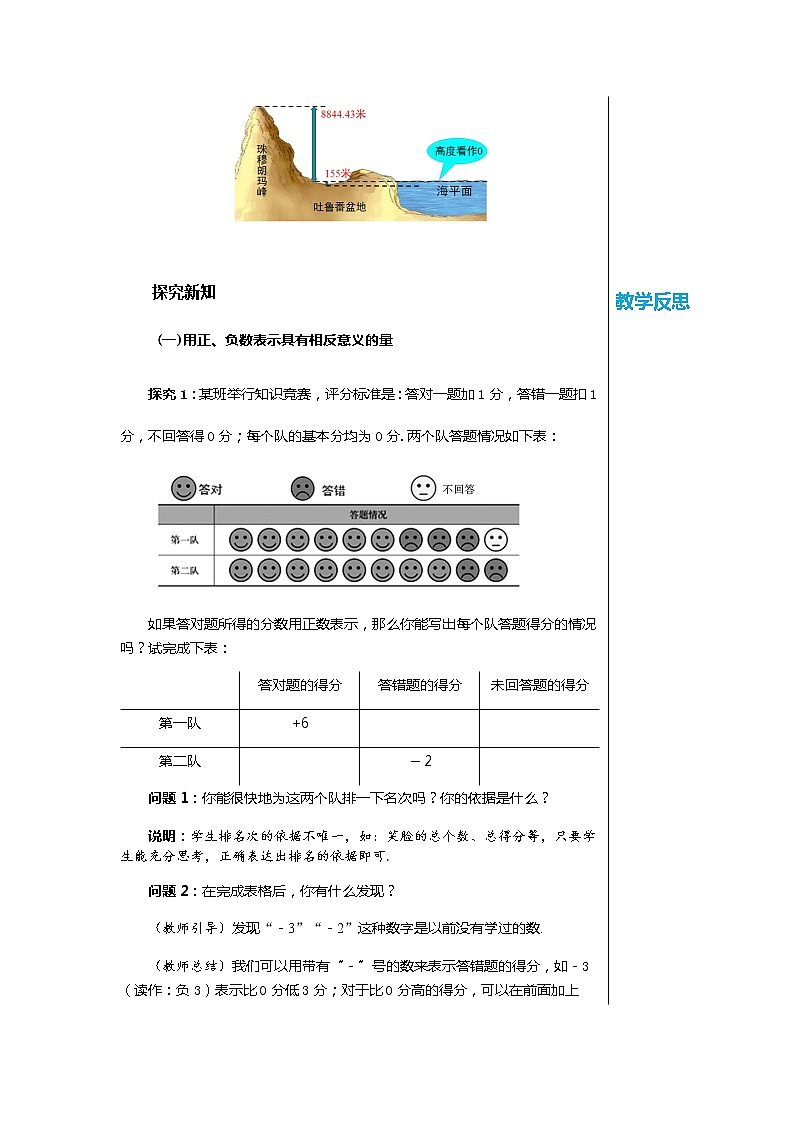
教学目标

1.使学生会判断正数与负数，理解有理数的意义.

2.让学生会用正、负数表示具有相反意义的量.

3.让学生能按一定的标准对有理数进行分类.

教学重难点

重点：1.理解并掌握有理数的概念.

2.会用正、负数表示生活中具有相反意义的量.

难点：1.负数的意义.

      2.有理数的分类.

教学过程

导入新课

用小学学过的数能表示下列数吗?

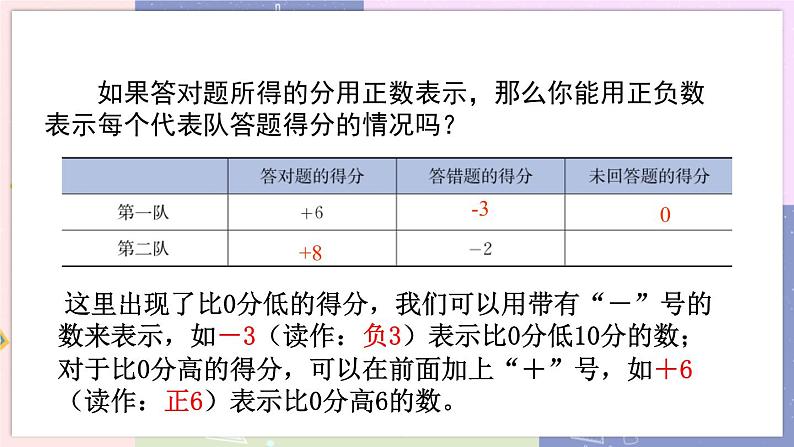
探究新知

 (一)用正、负数表示具有相反意义的量

探究1：某班举行知识竞赛，评分标准是：答对一题加1分，答错一题扣1分，不回答得0分；每个队的基本分均为0分.两个队答题情况如下表：

如果答对题所得的分数用正数表示，那么你能写出每个队答题得分的情况吗？试完成下表：

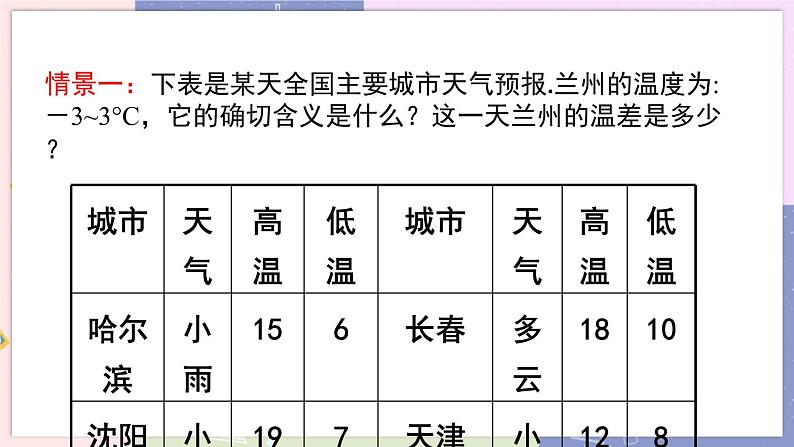
问题1：你能很快地为这两个队排一下名次吗？你的依据是什么？

说明：学生排名次的依据不唯一，如：笑脸的总个数、总得分等，只要学生能充分思考，正确表达出排名的依据即可.

问题2：在完成表格后，你有什么发现？

（教师引导）发现“－3”“－2”这种数字是以前没有学过的数.

（教师总结）我们可以用带有“－”号的数来表示答错题的得分，如－3（读作：负3）表示比0分低3分；对于比0分高的得分，可以在前面加上“＋”号，如＋6（读作：正6）表示比0分高6分.

注意：“＋”常常可以省略.

问题3：“－”可以省略吗？为什么？

（教师提问学生，最后给出明确答复）

不可以省略.“＋”和“－”是数的性质符号，“－”省略了，数的性质就改变了.

结论：像6，8，…这样的数叫做正数，它们都比0大；

在正数前面加上“－”号的数叫做负数，例如－3，－6，….

问题4：正数和负数有什么关系？

让学生通过对具有相反意义的量的讨论和对数学模型的观察、归纳、概括、交流等数学活动，进一步理解怎样用正、负数表示现实生活中具有相反意义的量，掌握正、负数的意义，培养学生正、负数的数感.

问题5：0是正数还是负数？

学生的回答会多种多样，甚至有的学生无法回答，这里教师明确告诉学生，引入负数以后，“0”的意义就不仅仅表示“没有”了，它还是正、负数的分界，是“基准”.

问题6：带“－”的数一定是负数吗？

学生回答该问题有一定困难.对于正数和负数的概念，要提醒学生注意不要认为带“＋”的数就是正数，带“－”的数就是负数.如－a不一定是负数.

探究2：下表是某天全国某些城市天气预报.兰州的温度为-3~3 ℃，它的确切含义是什么？这一天兰州的温差是多少？

（学生分组讨论，教师引导、总结，引出“零上”与“零下”是一组具有相反意义的量）

问题：同学们还能列举出具有“相反意义”的量吗？

零上与零下，盈利与亏损，加分与扣分，高出与低于，向东与向西，上升与下降，增加与减少，收入与支出，胜与负，前进与后退，多与少，重与轻……

例1   (1)某人转动转盘，如果用+5圈表示沿逆时针方向转了5圈，那么沿顺时针方向转了12圈怎样表示？

（2）在某次乒乓球质量检测中，一只乒乓球超出标准质量0.02克记作

＋0.02克，那么0.03克表示什么？

（3）某大米包装袋上标注着：“净重量：10 kg±150 g”， 这里的“10 kg±

150 g” 表示什么？

解：（1）沿顺时针方向转了12圈记作12圈；

（2）0.03克表示乒乓球的质量低于标准质量0.03克；

（3）每袋大米的标准质量为10 kg，但实际每袋大米可能有150 g的误差，即每袋大米的净含量最多是10 kg+150 g，最少是10 kg150 g.

（二）有理数的概念及分类

探究3：分组活动，列举已学过的数，然后将列举的所有数适当地分成几组，并说明这样分组的理由.

总结：

有理数的分类：

有理数(按定义)　　　

有理数(按性质)

整数和分数统称有理数.

例2  把下面各数填在相应的括号里：

正数集合{                        …}；

负数集合{                        …}；

整数集合{                        …}；

正分数集合{                      …}；

负分数集合{                      …}；

分数集合{                        …}.

解：

归纳：

有理数的分类中的四点注意：

1.相对性：正数是相对负数而言的，整数是相对分数而言的.

2.特殊性： 0既不是正数，也不是负数，0是整数.

3.多属性：同一个数，可能属于多个不同的集合.如5既是正数又是整数.

4.提醒：分数包括有限小数和无限循环小数.

课堂练习

1.零不是（    ）

A.非负数                  B.有理数 

C.正数                    D.整数

2.下列说法错误的是（    ）

A.0.5是分数              B.0不是正数也不是负数   

C.2.74是负分数           D.非负数就是正数

3.如果以每月生产180个零件为准，超过的零件数记为正数，不足的零件数记为负数，那么1月生产160个零件记为______个，2月生产200个零件记为______个.

4.一种商品的标准价格是200元，但随着季节的变化，商品的价格可浮动±10%.

(1)±10%的含义是什么？

(2)请你算出该商品的最高价格和最低价格.

(3)如果以标准价格为标准，超过标准记作“＋”，低于标准记作“－”，该商品价格的浮动范围又可以怎样表示？

5.下列各数：－2，5，，0.63，0，7，－0.05，－6，9，.  

其中正数有____个，负数有____个，正分数有____个，

负分数有____个，自然数有____个，整数有____个.

6.某公交车原有22人，经过3个站点时，上下车情况如下(上车为正，下车为负)：(4，8)，(5，6)，(3，2).

求经过3个站点后车上剩余的人数.

参考答案

1.C

2.D

3.20；+20

4.解：(1)±10%的含义是在标准价格的基础上加价或降价的幅度不超过10%.

(2)最高价格为200＋200×10%＝220(元)；最低价格为200－200×10%＝180(元).

(3)因为220－200＝20(元)，200－180＝20(元)，所以这件商品加价或降价的幅度不超过20元，所以这件商品价格的浮动范围又可以表示为200±20元.

5.6；4；3；2；4；6

6.解：第一站剩余人数为22＋4－8＝18(人)；

第二站剩余人数为18－5＋6＝19(人)；

第三站剩余人数为19－3＋2＝18(人).

故最后车上剩余18人.

课堂小结

1.用正、负数表示具有相反意义的量.

2.有理数的分类：

有理数(按定义)　　　

有理数(按性质)

布置作业

完成教材习题2.1.

板书设计

第二章  有理数及其运算

1  有理数

（一）正数、负数，具有相反意义的量

（二）有理数的分类

有理数(按定义)　　　

有理数(按性质)

教学反思

教学反思

教学反思

教学反思

教学反思