【中职专用】温州市中职基础模块上册单元复习 第二章 不等式（高教版）PPT课件

这是一份【中职专用】温州市中职基础模块上册单元复习 第二章 不等式（高教版）PPT课件，共31页。

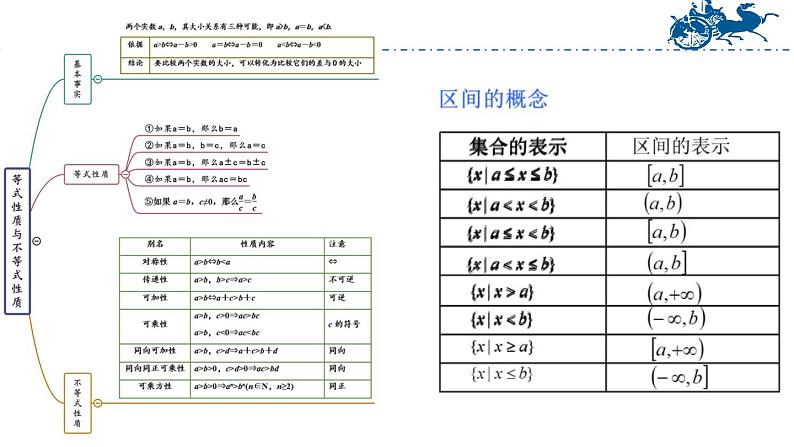
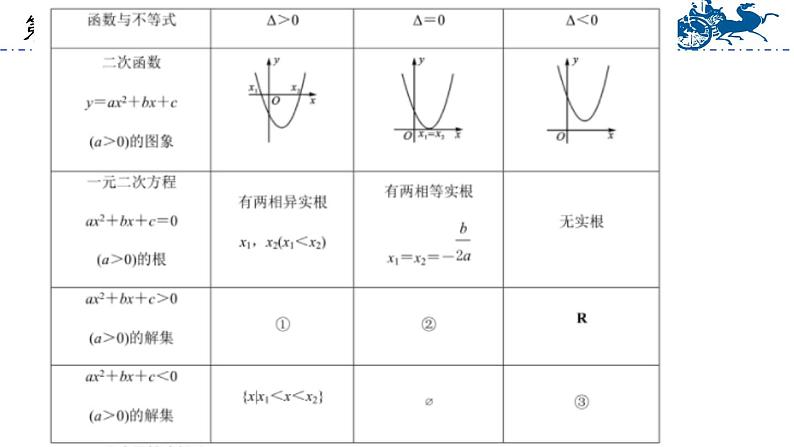
1《基础模块上册复习》数学第二章 不等式1．能用作差法比较比较两个实数或两个代数式的大小．2．理解不等式的基本性质，会用不等式的基本性质解决一些简单的问题．学习目标5.了解绝对值不等式的性质，会解形如|ax＋b|≥c和|ax＋b|≤c的绝对值不等式．4.会解一元二次不等式．3.会用区间表示集合．【例1】　已知b<0 C．－b<－a D．a－b>a＋b【思路点拨】　代值法D考点：不等式的性质【练习1】若a，b，c，d∈R，则下列关系正确的是(　　)A．a>b⇒ac>bc B．a>b⇒a2>b2C．a>b，c>d⇒ac>bd D．a>b，c>d⇒a－d>b－cD【练习2】若x>y>z，且x＋y＋z＝0，则下列不等式成立的是(　　)A．xyyz D．xy20， ∴ (x－2)2>x(x－4) .【练习1】　　比较 (x－2)2与3－2x的大小．考点：作差法比较大小基本步骤：作差→变形→判号→定论．【答案详解】　∵(x－2)2－ (3－2x) ＝x2－4x＋4－(3－2x)第7页，共29页【变式】定义一种新运算：a◎b＝ab＋a－b.(1)比较大小：3◎π________π◎3；(用“>”、“<”或“＝”填空)<【提示】 3◎π＝3π＋3－π，π◎3＝3π＋π－3.易得3◎π<π◎3.(2)试分析a◎b与b◎a的大小关系．(2)解：∵a◎b＝ab＋a－b，b◎a＝ab＋b－a，∴a◎b－b◎a＝(ab＋a－b)－(ab＋b－a)＝2(a－b)，∴当a>b时，a◎b>b◎a；当a＝b时，a◎b＝b◎a；当a0；　　　　(3)4x－x2<0.【归纳点评】　系数正，解两根，大于取两边，小于取中间。【答案详解】(1)原不等式等价于(x＋1)(x－4)≤0，解得－1≤x≤4，∴原不等式的解集为[－1，4]．(2)∵方程2x2＋5x＋4＝0的判别式Δ＝25－4×2×4＝－7<0，∴原不等式的解集为R.(3)原不等式可化为x2－4x>0，即x(x－4)>0，∴原不等式的解集为(－∞，0)∪(4，＋∞)．考点：一元二次不等式【例4】　　不等式|3－2x|<1的解集为(　　)A．(－2，2) B．(2，3) C．(1，2) D．(3，4)【思路点拨】利用|ax＋b|0)进行求解．C考点：绝对值不等式【练习2】解集为(－∞，0]∪[1，＋∞)的不等式(组)是(　　)A．x2－2x≥－1 B. C．|2x－1|≥1 D．x－ 2(x－1)≤3C【例5】已知不等式ax2－bx＋3≤0的解集为 ， 求a，b的值．【思路点拨】　解集中的端点值1和 是方程ax2－bx＋3＝0的两个根．【答案详解】　由题意可知a>0，且1和 是方程ax2－bx＋3＝0的两个根，∴故a，b的值分别是2，5.考点：不等式与方程的根【变式】若不等式|ax＋2|<6的解集为(－1，2)，则实数a等于(　　)A．－8 B．－4 C．2 D．6B考点：不等式与方程的根【提示】 原不等式等价于－60，则－ 0}，不满足题意，∴m≠0.②m≠0时，根据二次函数的图象性质得 ⇒m<－1，∴综上所述，实数m的取值范围是(－∞，－1)．【变式】若无论x取何值时，不等式x2－2kx＋4>0恒成立，则实数k的取值范围是(　　)A．(－∞，－2)∪(2，＋∞) B．(－∞，－4)∪(4，＋∞)C．(－4，4) D．(－2，2)D考点：恒成立问题等价：函数y=x2－2kx＋4的图像恒在x轴上方【变式1】已知对任意的x∈R，不等式mx2－2x＋m<0恒成立，求实数m的取值范围．考点：恒成立问题有解【变式2】已知存在x∈R，使函数y=mx2－2x＋m<0成立，求实数m的取值范围．【变式3】已知存在x∈R，使函数y=mx2－2x＋m<0成立，求实数m的取值范围．课后作业1．若a B．b2ab D．abb>c，则下列式子一定成立的是(　　)A．ac>bc B．a－c>b－c C. < D．a＋c＝2bB3．已知a>b，c>d>0，则下列不等式成立的是(　　)A． B． C．ac>bd D．a－c>b－d【提示】 举反例进行排除错误选项．B4．若a>|b|，且b<0，则下列不等式成立的是(　　)A．a＋b>0 B．a＋b<0 C．|a|<|b| D．b－a>0A5．若不等式ax>b的解集是 ，则a的取值范围是(　　)A．{a|a<0} B．{a|a≤0} C．{a|a>0} D．{a|a≥0}A6．一元二次不等式x2－4x＋3≥0的解集为(　　)A．(1，3) B．(－∞，1]∪[3，＋∞)C．[1，3] D．(－∞，－3]∪[－1，＋∞)B7．若一元二次不等式x2＋mx－6m<0的解集是(－3，2)，则m=(　　)A．2 B．－2 C．1 D．－1CB9．如图所示，在数轴上表示的区间与下列不等式的解集相同的是(　　) 第6题图A．x2－x－6≤0 B．x2－x－6≥0 C. D. ≥0D10．若某三角形两条边的长分别为2和6，第三边也为偶数，则这个三角形的周长为________.14【提示】 三角形两边之和大于第三边的性质，得出第三边为6.11．解下列不等式：(1)x－x2＋6>0; (2)2x2－5x＋9≥0. (3) |x＋1|＋1>0解：(1)原不等式可化为x2－x－6<0，即(x＋2)(x－3)<0，解得－2 － 1, ∴原不等式的解集为R.12．比较(2x－3)(x＋2)和x2＋x－7的大小．解：∵(2x－3)(x＋2)－(x2＋x－7) ＝2x2＋x－6－x2－x＋7 ＝x2＋1>0， ∴(2x－3)(x＋2)>x2＋x－7.13．已知不等式(a－2)x2＋2(a－2)x－4<0对任意的x∈R恒成立，求a的取值范围．解：当a－2＝0，即a＝2时，不等式为－4<0恒成立，即a＝2符合题意．当a－2≠0，即a≠2时，不等式(a－2)x2＋2(a－2)x－4<0对任意的x∈R恒成立必须满足开口向下，即a－2<0且Δ＝4(a－2)2－4(a－2)×(－4)<0，解得－20的解集为(－∞，－3) ∪(－2，＋∞)，求：(1)常数b的值；(2)不等式|bx＋a|≤3的解集解：(1)由题意得－3和－2是方程ax2＋bx＋24＝0的两个根，∴ 解得(2)不等式|bx＋a|≤3等价于－3≤20x＋4≤3，解得－ ≤x≤－ ，∴原不等式的解集为 .31谢谢观看！