江苏省扬州市仪征市2021-2022学年八年级下学期期中考试数学试卷(含解析)

2021-2022年度第二学期期中调研测试

八年级数学

一、选择题（本大题共有8小题，每小题3分，共24分，下面各题均有四个选项，其中只有一个是符合题意的．请将正确选项前的字母填涂在答题卡中相应的位置上．）

1. 下列常用APP的图标中，是中心对称图形的是（   ）

A.  B.  

C.  D.

2. 下列调查中，不适合采用全面调查方式的是（    ）

A. 了解新冠肺炎确诊病人同机乘客的健康情况

B. 调查某中学在职教师的身体健康状况

C. 疫情期间对进入校园的师生的测温检查

D. 检测某城市的空气质量状况

3. 为更好地反映长春市一周内新冠确诊病例人数的变化情况，一般采用（　　）

A. 条形统计图 B. 折线统计图

C. 扇形统计图 D. 统计表

4. 下列式子中是分式的是（    ）

A.  B.  C.  D.

5. 从一副扑克牌中任意抽取1张，下列4个事件：①这张牌是“A”；②这张牌是“红心”；③这张牌是“大王”；④这张牌是“红色的”．其中发生的可能性最大的事件是（　　）

A. ① B. ② C. ③ D. ④

6. 下列结论中，矩形具有而菱形不一定具有的性质是（   ）

A. 内角和为360° B. 对角线互相平分 C. 对角线相等 D. 对角线互相垂直

7. 若关于x的分式方程有增根，则增根为（    ）

A. 1 B. 0 C. 1和0 D. 不确定

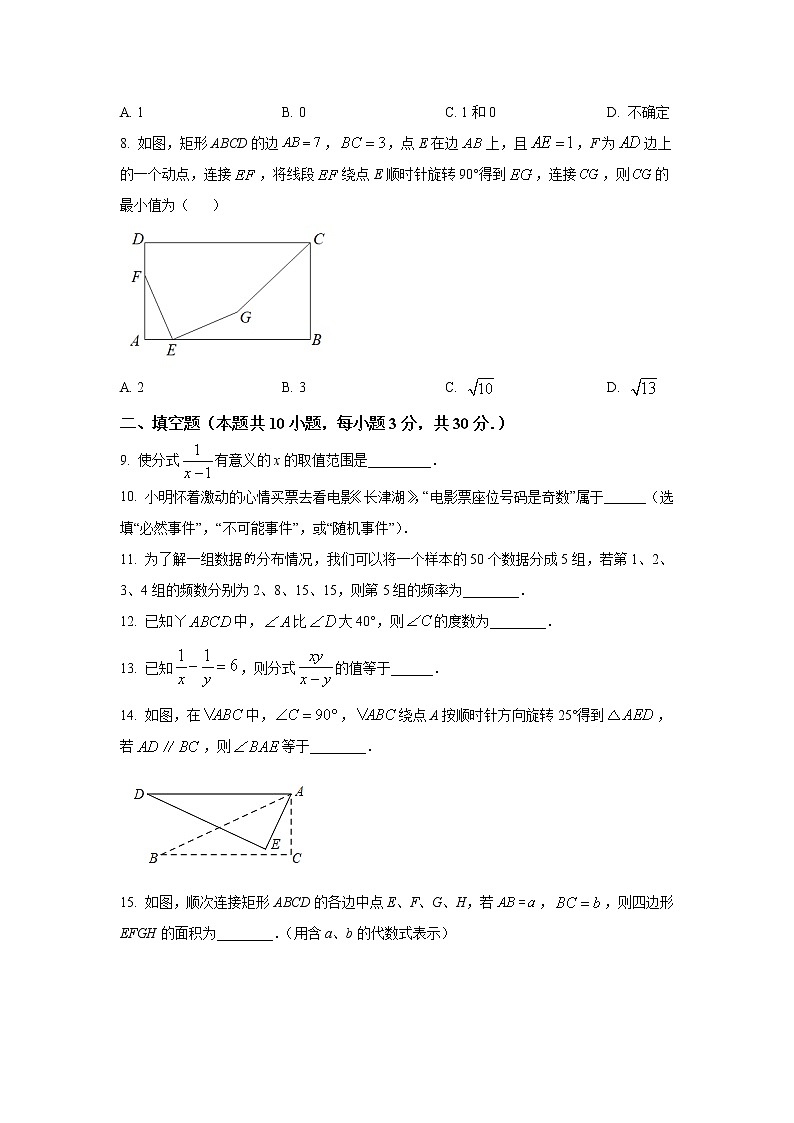
8. 如图，矩形ABCD的边，，点E在边上，且，F为边上的一个动点，连接，将线段绕点E顺时针旋转90°得到，连接，则的最小值为（    ）

A. 2 B. 3 C.  D.

二、填空题（本题共10小题，每小题3分，共30分．）

9. 使分式有意义的x的取值范围是_________．

10. 小明怀着激动的心情买票去看电影《长津湖》，“电影票座位号码是奇数”属于______（选填“必然事件”，“不可能事件”，或“随机事件”）．

11. 为了解一组数据分布情况，我们可以将一个样本的50个数据分成5组，若第1、2、3、4组的频数分别为2、8、15、15，则第5组的频率为________．

12. 已知中，比大40°，则的度数为________．

13. 已知，则分式的值等于______．

14. 如图，在中，，绕点A按顺时针方向旋转25°得到，若，则等于________．

15. 如图，顺次连接矩形ABCD的各边中点E、F、G、H，若，，则四边形EFGH的面积为________．（用含a、b的代数式表示）

16. 如图，在矩形ABCD中，BE平分∠ABC，EC平分∠BED．若，则的长为________．

17. 关于x的方程＝2的解是非负数，则a的取值范围是_____．

18. 已知平面直角坐标系中，点A、B在动直线（m为常数且）上，，点C是平面内一点，以点O、A、B、C为顶点平行四边形面积的最大值是________．

三、解答题（本大题共10小题，共计96分．请在答题卡指定区域内作答，解答时应写出必要的演算步骤、证明过程或文字说明）

19. 解方程

（1）

（2）

20. 先化简，然后从，0，1，3中选一个合适数代入求值．

21. 在一只不透明的口袋里，装有若干个除了颜色外均相同的小球，某数学学习小组做摸球试验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复．下表是活动进行中的一组统计数据：

（1）上表中的a=________，b=________；

（2）“摸到白球的”的概率的估计值是________（精确到0.1）；

（3）如果袋中有18个白球，那么袋中除了白球外，还有多少个其它颜色的球？

22. 某中学为了解全校1600名学生到校上学的方式，在全校范围随机抽取了若干名学生进行调查，调查过程中提供了五种上学方式：“步行、自行车、公交车、私家车、其他”供每一位被调查的学生选择，每人只能选其中一项，且不能不选．现将调查得到的结果绘制成如图所示的条形统计图和扇形统计图．

（I）在这次随机调查中，样本容量为　　　　；

（2）补出条形统计图中上学方式为“步行”的部分；

（3）扇形统计图中上学方式为“公交车”部分的圆心角度数等于　　　　°；

（4）估计该中学全校所有学生中上学方式为“私家车”的人数等于　　　　．

23. 如图所示的正方形网格中，ABC的顶点均在格点上，请在所给直角坐标系中按要求画图和解答下列问题：

（1）将ABC沿x轴翻折后再沿y轴向上平移2个单位，在图中画出平移后的A1B1C1，若ABC内有一点P(a，b)，则经过两次变换后点P的坐标变为           ；

（2）作出ABC关于坐标原点O成中心对称的A2B2C2；

（3）若将ABC绕某点逆时针旋转90°后，其对应点分别为A3(﹣1，﹣2)，B3(1，﹣3)，C3(0，﹣5)，则旋转中心坐标为           ．

24. 甲、乙两公司为“见义勇为基金会”各捐款30000元．已知甲公司的人数比乙公司的人数多20%，乙公司比甲公司人均多捐20元．甲、乙两公司各有多少人？

（1）利用表格分析数量关系是解决分式方程问题的重要手段，填表：（不需要化简）

（2）写出完整的解答过程．

25. 如图，在中，∠BAC＝90°，DE是中位线，AF是的中线．求证DE＝AF．

证法1：∵DE是的中位线，

∴DE＝     ．

∵AF是的中线，∠BAC＝90°，

∴AF＝      ，

∴DE＝AF．

请把证法1补充完整，连接EF，DF，试用不同的方法证明DE＝AF

证法2：

26. 如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF．

（1）求证：AF＝DC；

（2）△ABC满足什么条件时，四边形ADCF是菱形，并说明理由．

27. 阅读下列材料：通过小学的学习我们知道，分数可分为“真分数”和“假分数”．而假分数都可化为带分数，如：．我们定义：在分式中，对于只含有一个字母的分式，当分子的次数大于或等于分母的次数时，我们称之为“假分式”；当分子的次数小于分母的次数时，我们称之为“真分式”．如：，这样的分式就是假分式；再如：，这样的分式就是真分式．类似的，“假分式”也可以化为“带分式”（即：整式与真分式的和的形式）．

如：；

再如：．

解决下列问题：

（1）分式是________分式（填“真”或“假”）；

（2）请将假分式化为带分式的形式；

（3）若分式的值为整数，求满足条件的整数x的值．

28. 如图1，在正方形中，边，点P、Q、E分别在、、上（E不与A、D重合）

（1）如图2，当点Q与C重合，且时，求证：；

（2）如图3，若将四边形沿翻折，使点B落在E点处，连接、，．

①若，求的长；

②求四边形面积S的取值范围．

答案

1. B

解：A、不是中心对称图形，故本选项不合题意；

B、是中心对称图形，故本选项符合题意；

C、不是中心对称图形，故本选项不合题意；

D、不是中心对称图形，故本选项不合题意；

故选：B．

2. D

解：A、了解新冠肺炎确诊病人同机乘客的健康情况，适合采用全面调查方式，故本选项不符合题意；

B、调查某中学在职教师的身体健康状况，适合采用全面调查方式，故本选项不符合题意；

C、对全校同学进行每日温度测量统计，适合采用全面调查方式，故本选项不符合题意；

D、检测某城市的空气质量状况，不适合采用全面调查方式，故本选项符合题意；

故选：D．

3. B

解：为了更好地反映某地一周内新冠确诊病例人数的变化情况，一般选用折线统计图，

故选：B．

4. C

解：A、它的分母中不含有字母，是整式，故本选项不符合题意；

B、它的分母中不含有字母，是整式，故本选项不符合题意；

C、它是分式，故本选项符合题意；

D、它是分数，故本选项不符合题意；

故选：C．

5. D

解：∵①这张牌是“A”的概率为 ；

②这张牌是“红心”的概率为；

③这张牌是“大王”的概率为；

④这张牌是“红色的”的概率为．

∴其中发生的可能性最大的事件是④．

故选：D．

6. C

A、菱形、矩形的内角和都为360°，故本选项错误；

B、对角互相平分，菱形、矩形都具有，故本选项错误；

C、对角线相等菱形不具有，而矩形具有，故本选项正确；

D、对角线互相垂直，菱形具有而矩形不具有，故本选项错误；

故选：C

7. A

解：，

解得：，

∵若关于x的分式方程有增根，

∴，

解得：，故A正确．

故选：A．

8. D

解：将△AEF绕点E顺时针旋转90°得到△HEG，延长HG交BC于点N，

∴AE=HE=1，AF=HG，∠A=∠H=∠AEH=90°，

∴HG∥AB，

则点G在平行于AB，且与AB距离为1的直线上运动，

∴当HG=AD=3时，GC有最小值，

∵∠HEB=∠B=∠EHN=90°，

∴四边形EHNB是矩形，

∴HE=BN=1，BE=HN=6，

∴CN=2，GN=3，

∴CG=，

故选：D．

9. x≠1

根据题意得：x-1≠0，即x≠1.

故答案为：x≠1．

10. 随机事件

解：小明怀着激动的心情买票去看电影《长津湖》，“电影票座位号码是奇数”属于随机事件，

故答案为：随机事件．

11. 20%

解：由题意得：

50-2-8-15-15=10，

10÷50=0.2，

∴第5组的频率为：20%，

故答案为：20%．

12. 110°

解：∵四边形ABCD是平行四边形，

∴∠A＝∠C，AB//CD

∴∠A+∠D＝180°，

∵∠A-∠D＝40°，

∴∠A＝110°，

∴∠C＝110°；

故答案为：110°

13.

解：∵，

∴，

∴x－y=－6xy，

∴==，

故答案为：．

14. ##度

解：∵绕点A按顺时针方向旋转得到，

∴，

∵，

∴，

∵中，，

∴，

∴，

故答案为：．

15.

解：∵点E、F、G、H分别是矩形ABCD各边上的中点，且AB=a，BC=b，

∴AE=ED=BG=GC=b，AF=FB=DH=HC=a，

∴S△AEF= S△BFG= S△CGH= S△DFH=•a•b=ab，

∴S四边形EFGH= S矩形ABCD-4 S△AEF

= ab-4×ab=ab．

故答案是：ab．

16.

解：过点C作CF⊥BE于点F，

∵BE平分∠ABC，

∴∠ABE=∠CBF=45°，

∴AB=AE=1，

∴BE=，

∵四边形ABCD是矩形，

∴AB=CD=1，

∵EC平分∠BED，

∴CF=CD=1，

∵∠CBF=45°，

∴BF=CF=1，

∴由勾股定理可知：BC=，

∴AD=BC=，

故答案为：．

17. 且．

解：去分母得： ，

解得：，

由分式方程的解为非负数，得到且，

解得：且．

故答案为：且．

18. 30

解：∵直线AB：y＝mx﹣6m+8＝m（x﹣6）+8，

∴AB过定点M（6，8），

∴，

作OH⊥AB于H，

∴OH≤10，

∴S△ABO＝，

即△ABO的最大面积是15，

∵以点O、A、B、C为顶点的平行四边形面积是△ABO面积的2倍，

∴以点O、A、B、C为顶点的平行四边形面积的最大值是30．

故答案为：30．

19. （1）解：方程两边乘（x+3）（x-1），得2x-2=x+3，

解得：x=5，

检验：当x=5时，（x+3）（x-1）≠0，

所以x=5是原分式方程的解，

即原分式方程的解是x=5；

（2）解：方程两边乘x-4，得5-x=x-4+1，

解得：x=4，

检验：当x=4时，x-4=0，

所以x=4是原分式方程的增根，原分式方程无解．

20. 原式

分式的分母不能为0

解得：m不能为，0，3

则选代入得：原式．

21. （1）解：a=59÷100=0.59，b=200×0.58=116．
故答案为：0.59，116；

（2）解：“摸到白球的”的概率的估计值是0.6；

故答案为：0.6；

（3）解：18÷0.6-18=12（个）．

答：除白球外，还有大约12个其它颜色的小球．

22. （1）这次随机调查中抽取的总人数是：12÷15%=80（人），

则样本容量为80．

故答案为：80；

（2）步行的人数有：80×20%=16（人），补全统计图如下：

（3）公交车的人数有：80﹣12﹣16﹣20﹣6=26（人），

扇形统计图中上学方式为“公交车”部分的圆心角度数等于：360°117°．

故答案为：117；

（4）根据题意得：

1600400（人），

答：该中学全校所有学生中上学方式为“私家车”的人数等于400人．

故答案为：400．

23. 解：（1）如图，△A1B1C1，经过两次变换后点P的坐标变为（a，﹣b+2）．

故答案为：（a，﹣b+2）．

（2）如图，△A2B2C2即为所求作．

（3）如图，旋转中心的Q的坐标为（0，﹣1）．

故答案为：（0，﹣1）．

24. （1）

解：设乙公司员工人数为x，

甲公司员工人数=，

甲公司人均捐款=，

乙公司人均捐款=；

（2）

解：设乙公司员工人数为x，则甲公司员工人数为；

-=20

解得：x=250

检验：当x=250时，≠0，

∴x=250是原分式方程的解；

=300，

答：甲公司有300人，乙公司有250人．

25. 证法1：∵DE是△ABC的中位线，

∴DE=BC，

∵AF是△ABC的中线，∠BAC=90°，

∴AF=BC，

∴DE=AF，

证法2：连接DF、EF，

∵DE是△ABC的中位线，AF是△ABC的中线，

∴DF、EF是△ABC的中位线，

∴DF∥AC，EF∥AB，

∴四边形ADFE是平行四边形，

∵∠BAC=90°，

∴四边形ADFE是矩形，

∴DE=AF．

故答案为：BC；BC．

26. 解：（1）证明：∵AF∥BC，
∴∠AFE=∠DBE，
∵E是AD的中点，
∴AE=DE，
在△AFE和△DBE中，

，

∴△AFE≌△DBE（AAS）；
∴AF=DB，
∵AD是BC边上的中线，
∴DB=DC
∴AF=DC
（2）AC⊥AB，
理由如下：
∵AF=DC，AF∥BC，
∴四边形ADCF是平行四边形，
∵AC⊥AB，AD是斜边BC的中线，
∴AD=BC=DC，
∴平行四边形ADCF是菱形．

27. （1）

分式是真分式．

故答案为：真

（2）

原式=

=

=

=

（3）

原式=

=

=

=

=

∵分式的值为整数，

即=－2，－1，1，2

解得：x =－1，0，2，3

∴整数x的值为－1，0，2，3．

28. （1）

证明：∵四边形ABCD是正方形，

∴AB=BC，∠A=∠CPB=90°，

∵BE⊥PC，

∴∠ABE+∠AEB=90°，∠ABE+∠BPC=90°，

∴∠AEB=∠BPC，

∴△BAE≌△CNP（AAS），

∴BE=PC；

（2）

解：①如图2中，连接PE．

∵PQ垂直平分线段BE，

∴PB=PE，设PB=PE=x，

在Rt△PAE中，∵AE2+AP2=PE2，

∴12+（3-x）2=x2，

∴x=，

∴PB=；

②如图3中，过点Q作QH⊥AB于H．

∵PQ⊥BE，QH⊥AB，

∴∠A=∠QHP=90°，

∴∠QPH+∠ABE=90°，∠ABE+∠AEB=90°，

∴∠QPH=∠BEA，

∵∠C=∠CBH=∠QHB=90°，

∴四边形BCQH是矩形，

∴BC=HQ=AB，

∴△BAE≌△QHP（AAS），

∴BE=PQ，

∵BE⊥PQ，

∴S四边形PEQB=BE2，

∵E不与A、D重合，

∴3＜BE＜3，

∴＜SB＜9．