初中数学人教版七年级下册8.2 消元---解二元一次方程组教学课件ppt

这是一份初中数学人教版七年级下册8.2 消元---解二元一次方程组教学课件ppt，共20页。PPT课件主要包含了知识要点，代入法的简单应用，怎么求xy的值呢，用一元一次方程求解，解得x5，用二元一次方程组求解，将③代入②得，代入y8-x，得y3，二元一次方程组等内容，欢迎下载使用。
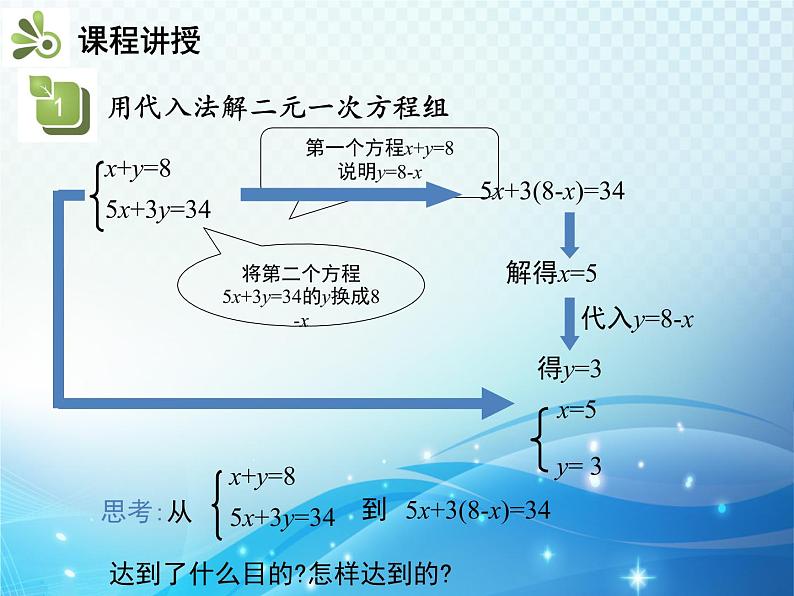
1.用代入法解二元一次方程组
1.什么是二元一次方程的解？使二元一次方程两边的值相等的两个未知数的值，叫作二元一次方程的解.2.什么是二元一次方程组的解？二元一次方程组的两个方程的公共解，叫作二元一次方程组的解.
昨天,我们8个人去红山公园玩,买门票花了34元.
每张成人票5元,每张儿童票3元.他们到底去了几个成人、几个儿童呢?
设他们中有x个成人，y个儿童.
5x+3(8-x)=34
解：设去了x个成人，则去了(8－x)个儿童，根据题意，得：
将x=5代入8－x=8－5=3.
答：去了5个成人， 3个儿童.
x+y=8，5x+3y=34
解：设去了x个成人，去了y个儿童，根据题意，得
二元一次方程组和一元一次方程有何联系？这对你解二元一次方程组有何启示？
由①得y = 8－x. ③
5x+3(8－x)=34.
把x = 5代入③得 y = 3.
x+y=8①5x+3y=34②
x+y=85x+3y=34
第一个方程x+y=8说明y=8-x
将第二个方程5x+3y=34的y换成8-x
消除其中一个未知数，将二元一次方程组转化成解一元一次方程的想法，叫做消元思想.
从一个方程中求出某一个未知数的表达式，再把它“代入”另一个方程，进行求解.这种方法称为代入消元法，简称代入法.
将y=-1代入 ③，得 x=2.所以原方程组的解是
解：由①，得 x=y+3. ③ 把 ③代入②，得 3（y+3）-8y=14. 解这个方程，得 y=-1.
用代入法解方程组 较简单的方法是(　　) A．消y　 B．消x　 C．消x和消y一样　 D．无法确定
根据市场调查，某种消毒液的大瓶装（500 g）和小瓶装（250 g）两种产品的销售数量（按瓶计算）比为2：5．某厂每天生产这种消毒液22.5 t，这些消毒液应该分装大、小瓶两种产品各多少瓶？
解：设这些消毒液应该分装x大瓶、y小瓶.
解得 x=20 000
答：这些消毒液应该分装20 000大瓶和50 000小瓶.
上面解方程组的过程可以用下面的框图表示：
y=2x　　x+y=12　
2x=y-54x+3y=65
3.有甲、乙两种货车，3辆甲种货车与4辆乙种货车一次可运货23 t，1辆甲种货车与5辆乙种货车一次可运货15 t.求甲、乙两种货车每辆一次分别可运货多少吨.
解：设甲种货车每辆一次可运货x t，乙种货车每 辆一次可运货y t.
答：甲种货车每辆一次可运货5 t，乙种货车每辆一次可运货2 t.