初中数学鲁教版 (五四制)七年级上册3 简单的轴对称图形集体备课课件ppt

这是一份初中数学鲁教版 (五四制)七年级上册3 简单的轴对称图形集体备课课件ppt，共23页。PPT课件主要包含了做一做，CECD，议一议，想一想，辨一辨，BDCD，不必再证全等，开拓创新试一试，练一练，回味无穷等内容，欢迎下载使用。

1.掌握角平分线性质的应用； 2.探索角的平分线的性质进行计算。3.能用尺规作已知角的平分线
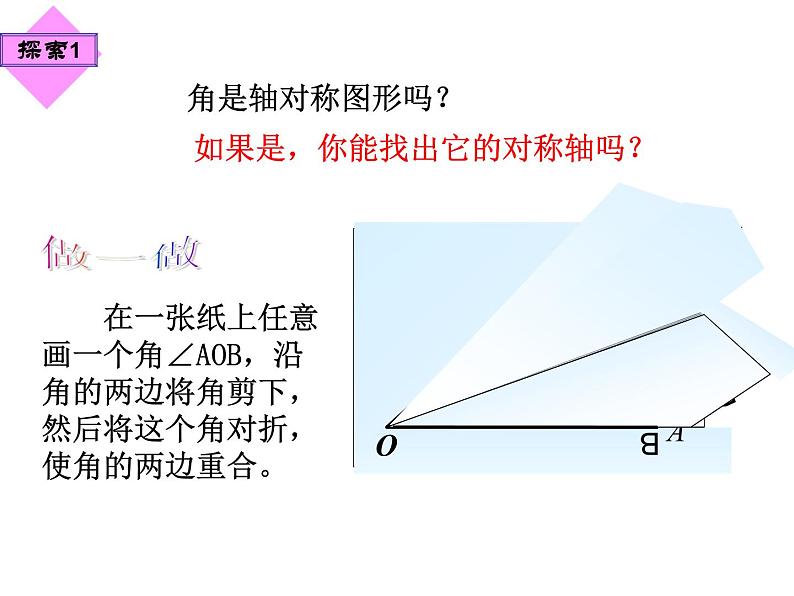
如果是，你能找出它的对称轴吗？
在一张纸上任意画一个角∠AOB，沿角的两边将角剪下，然后将这个角对折，使角的两边重合。
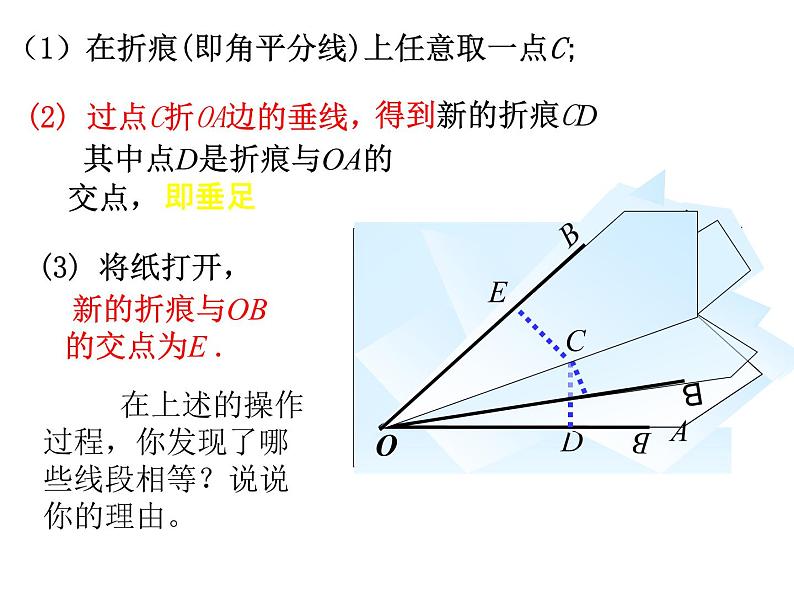
新的折痕与OB 的交点为E .
(2) 过点C折OA边的垂线，
其中点D是折痕与OA的 交点，
（1）在折痕(即角平分线)上任意取一点C;
在上述的操作过程，你发现了哪些线段相等？说说你的理由。
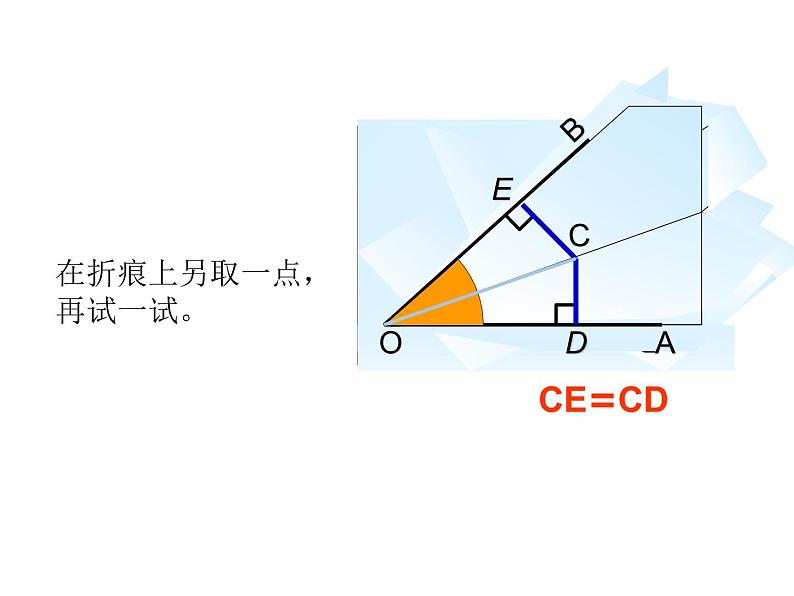
在折痕上另取一点，再试一试。
结论： 角是轴对称图形，就是它的对称轴。
那么角平分线有什么性质呢？
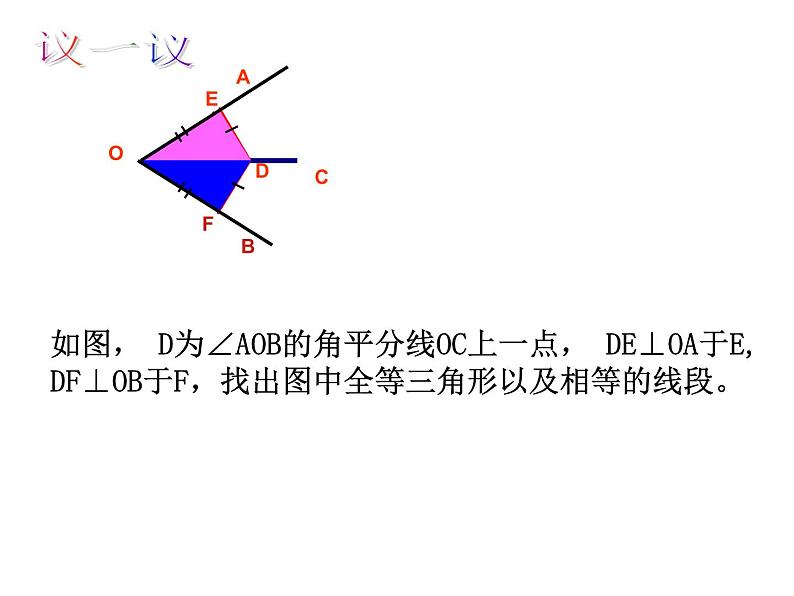
如图， D为∠AOB的角平分线OC上一点， DE⊥OA于E, DF⊥OB于F，找出图中全等三角形以及相等的线段。
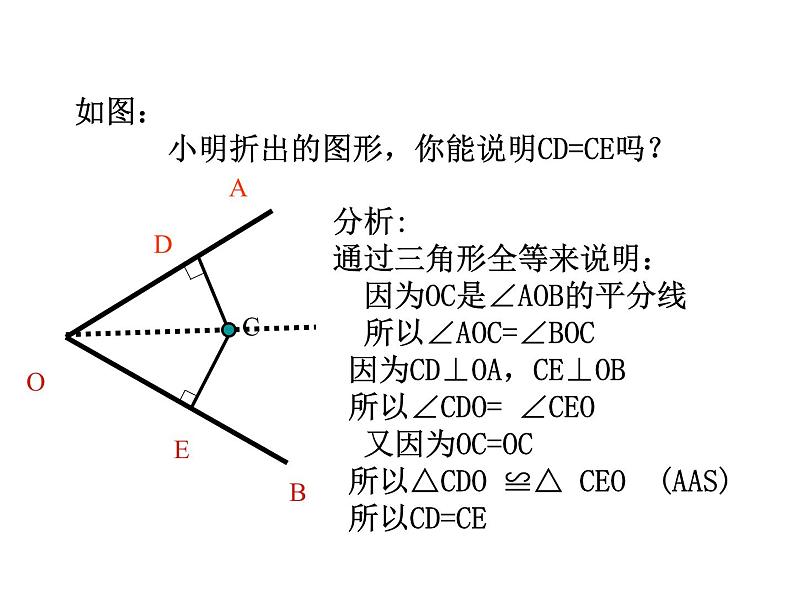
如图： 小明折出的图形，你能说明CD=CE吗？
分析:通过三角形全等来说明： 因为OC是∠AOB的平分线 所以∠AOC=∠BOC 因为CD⊥OA，CE⊥OB 所以∠CDO= ∠CEO 又因为OC=OC 所以△CDO ≌△ CEO (AAS) 所以CD=CE
角的平分线上的点到这个角的两边的距离相等
实际体会角的轴对称性和角的平分线上的点的性质
如图，OC平分∠AOB，PD与PE相等吗？
（1）∵ 如图，AD平分∠BAC（已知）
∴ = ，( )
在角的平分线上的点到这个角的两边的距离相等。
（2）∵ 如图， DC⊥AC，DB⊥AB （已知）
（3）∵ AD平分∠BAC, DC⊥AC，DB⊥AB （已知）
∴ = ，（ ）
⒈如图，在Rt△ABC中，∠C=90°，BD 是∠B的平分线，DE⊥AB,垂足为E，DE与DC相等吗？说明理由。
分析:因为BD是∠ABC的角平分线在Rt△ABC中， ∠C=90°，所以DC⊥BC又因为DE⊥AB所以DE=DC
有一个简易平分角的仪器（如图），其中AB=AD,BC=DC,将A点放角的顶点，AB和AD沿AC画一条射线AE,AE就是∠BAD的平分线，为什么？
怎样用尺规作一个角的平分线？
用尺规作角的平分线的方法
　　１．以Ｏ为圆心，适当长为半径作弧，交ＯＡ于Ｍ，交ＯＢ于Ｎ．
思考：某一个星期六，某中学初一年级的同学参加义务劳动，其中有四个班的同学分别在M、N两处参加劳动，另外四个班的同学分别在道路AB、AC两处劳动，现要在道路AB、AC的交叉区域内设一个茶水供应点P ，使P到两条道路的距离相等，且使 PM= PN，请你找出点P的位置，并说明理由。
1、如图， ∵ OC是∠AOB的平分线， 又 ________________∴PD=PE ( )
PD⊥OA，PE⊥OB

3、已知△ABC中, ∠C=900,AD平分∠ CAB,且 DC=8,求点D到AB的距离是多少？
◆这节课我们学习了哪些知识？
1、角的平分线的性质： 角的平分线上的点到角的两边的距离相等。
∵ OC是∠AOB的平分线, 又 PD⊥OA,PE⊥OB∴ PD=PE(角的平分线上的点到角的两边距离相等).
2、“作已知角的平分线”的尺规作图；