人教版八年级下册第十七章 勾股定理17.1 勾股定理完美版课件ppt

这是一份人教版八年级下册第十七章 勾股定理17.1 勾股定理完美版课件ppt，共20页。PPT课件主要包含了情景引入，边特殊，角特殊，勾股定理，新知探究，a2+b2c2，方法1补形法，方法2割形法，∵S大正方形＝c2，赵爽弦图等内容，欢迎下载使用。

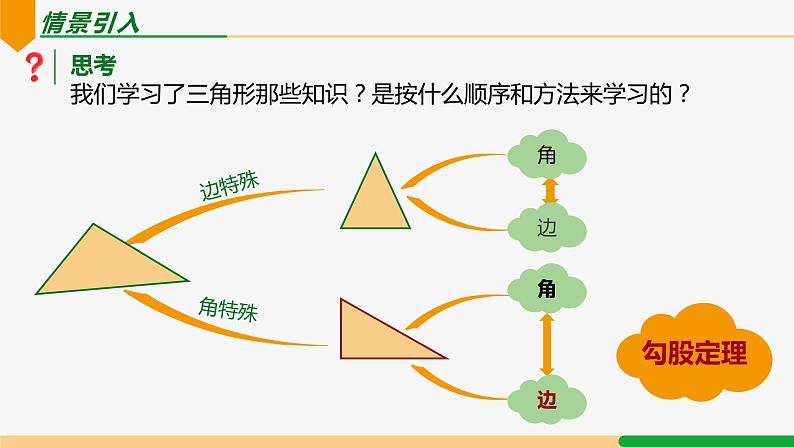
思考 我们学习了三角形那些知识？是按什么顺序和方法来学习的？
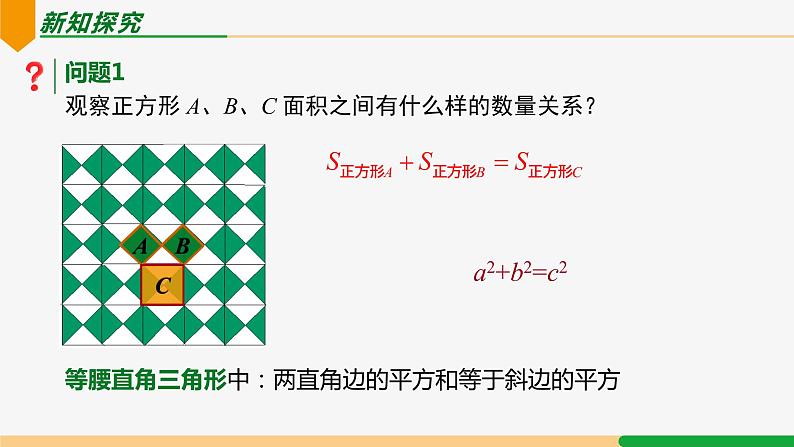
问题1 观察正方形 A、B、C 面积之间有什么样的数量关系？
等腰直角三角形中：两直角边的平方和等于斜边的平方
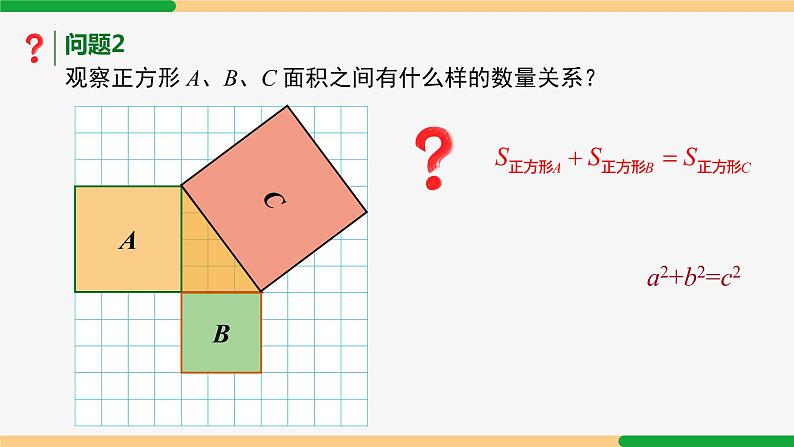
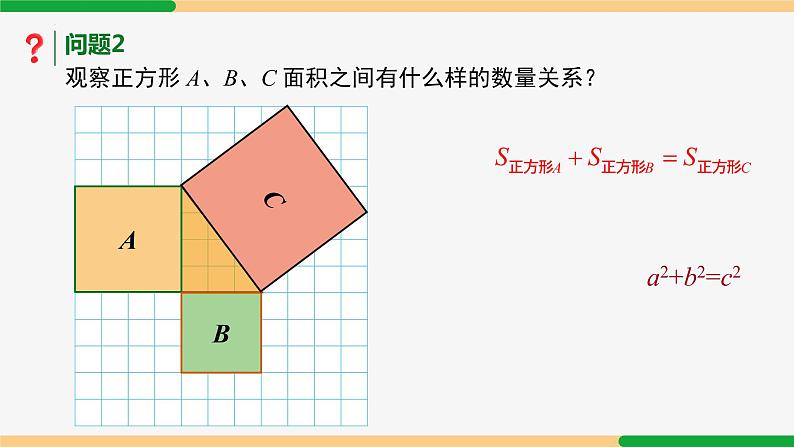
问题2 观察正方形 A、B、C 面积之间有什么样的数量关系？
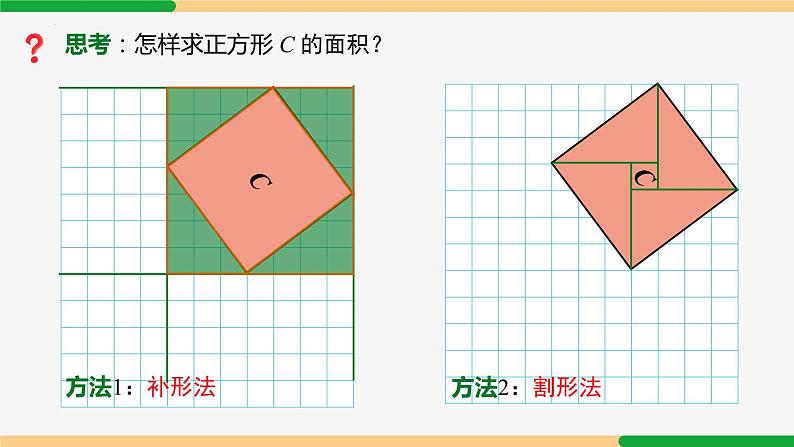
思考：怎样求正方形 C 的面积？
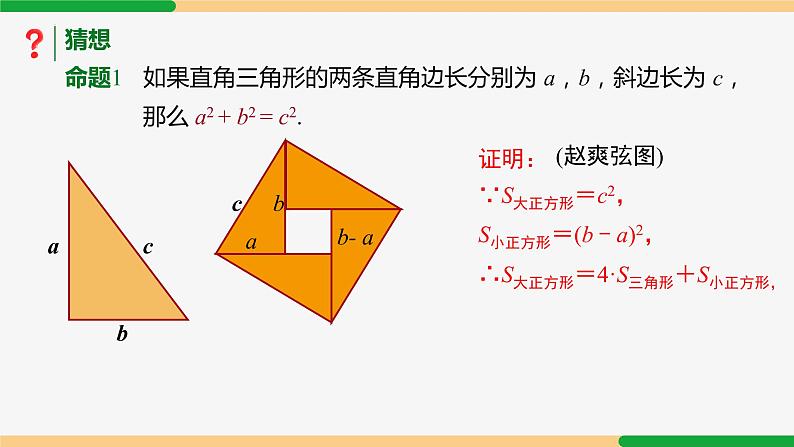
猜想 命题1 如果直角三角形的两条直角边长分别为 a，b，斜边长为 c，那么 a2 + b2 = c2.
S小正方形＝(b - a)2，
∴S大正方形＝4·S三角形＋S小正方形，
勾股定理(毕达哥拉斯定理).
如果直角三角形的两条直角边长分别为 a，b，斜边长为 c，那么 a2 + b2 = c2.
在Rt△ABC中，∠C=90°.
∴ a2 + b2 = c2.
例1 如图，在 Rt△ABC 中， ∠C = 90°.
(1) 若 a = b = 5，求 c；
(2) 若 a = 1，c = 2，求 b.
例2 求下列图中表示边长的未知数S1、S2、a 的值.
(1) (2) (3)
解：(1)S1100；
(2) S225 ；
(3) a7.
例3 在Rt△ABC中，AB＝4，AC＝3，求BC的长.
解：本题斜边不确定，需分类讨论：当 AB 为斜边时，如图①，当 BC 为斜边时，如图②，
例4 已知∠ACB = 90°，CD⊥AB，AC = 3，BC = 4. 求 CD 的长.
解：由勾股定理可得AB2 = AC2 + BC2 = 25， 即 AB = 5.根据三角形面积公式，∴ AC×BC = AB×CD.∴ CD = .
求线段长度的两个常用方法.
法一：勾股定理 ∴ a2 + b2 = c2.
法二：面积法 ∴ AC×BC = AB×CD.
方法近400种，多以面积法(勾股弦图).
在Rt△ABC中，∠C=90°.a2 + b2 = c2.
1.下列说法中，正确的是 （ ）A. 已知 a，b，c 是三角形的三边，则 a2 + b2 = c2B. 在直角三角形中两边和的平方等于第三边的平方C. 在 Rt△ABC 中，∠C = 90°，所以 a2 + b2 = c2D. 在 Rt△ABC 中，∠B = 90°，所以 a2 + b2 = c2
2. 图中阴影部分是一个正方形，则此正方形的面积为 .
3. 在 △ABC 中，∠C = 90°.(1) 若 a = 15，b = 8，则 c = . (2) 若 c = 13，b = 12，则 a = .4. 若直角三角形中，有两边长是 5 和 7，则第三边长的平方为_______.
5. 如图中未知数 x = .
6.如图，在△ABC中，AD⊥BC，∠B=45°，∠C=30°，AD=1，求△ABC的周长．
解：∵AD⊥BC，∴∠ADB=∠ADC=90°．在Rt△ADB中，∵∠B+∠BAD=90°，∠B=45°，∴∠B=∠BAD=45°，∴BD=AD=1，∴AB= ．在Rt△ADC中，∵∠C=30°，∴AC=2AD=2，∴CD= ，∴BC=BD+CD=1+ ，∴△ABC的周长=AB+AC+BC= ．