人教版八年级下册17.1 勾股定理优质课件ppt

这是一份人教版八年级下册17.1 勾股定理优质课件ppt，共22页。PPT课件主要包含了学习目标，课前导入，勾股定理，如何证明呢，勾股定理的证明，∵S大正方形＝c2，勾股定理的有关计算，巩固练习，c13，a20等内容，欢迎下载使用。

1.经历勾股定理的探究过程，了解关于勾股定理的一 些文化历史背景，会用面积法来证明勾股定理，体 会数形结合的思想.（重点）2.会用勾股定理进行简单的计算 .（难点）
毕达哥拉斯在朋友家里做客时，从砖铺成的地面中发现了直角三角形三边的数量关系．我们也来观察一下，看看从中能发现什么？
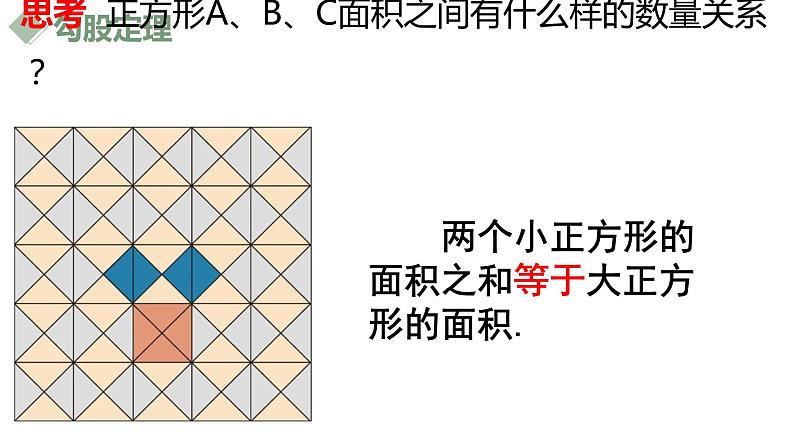
思考 正方形A、B、C面积之间有什么样的数量关系？
两个小正方形的面积之和等于大正方形的面积.
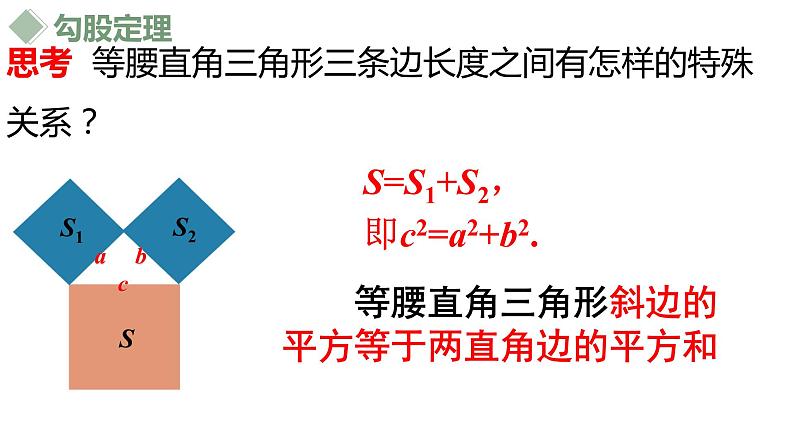
思考 等腰直角三角形三条边长度之间有怎样的特殊关系？　
等腰直角三角形斜边的平方等于两直角边的平方和
a b c
S=S1+S2，即c2=a2+b2.
思考 在网格中一般的直角三角形，以它的三边为边长的三个正方形A、B、C 是否也有类似的面积关系？观察下图(每个小正方形的面积为单位1)：
证法1：我国古代证明该命题的“赵爽弦图”
赵爽指出：按弦图，又可以勾股相乘为朱实二，倍之为朱实四.以勾股之差自相乘为中黄实.加差实，亦成弦实.
S小正方形＝(b-a)2,
∴S大正方形＝4·S三角形＋S小正方形，
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智，它是我国古代数学的骄傲.因为，这个图案被选为2002年在北京召开的国际数学大会的会徽.
由此证明了命题1是正确的，又因为该命题与直角三角形的边有关，我国把它称为勾股定理.在西方则称为毕达哥拉斯定理.
1.如图，在Rt△ABC中， ∠C=90°.
（1）若a=b=5,求c;
（2）若a=1,c=2,求b.
解：(2)据勾股定理，得
1.设直角三角形的两条直角边长分别为a和b，斜边长为c.（1）已知a=6，c=10，求b；（2）已知a=5，b=12，求c；（3）已知c=25，b=15，求a.
3.如图，在△ABC中，AD⊥BC，∠B=45°，∠C=30°， AD=1，求△ABC的周长．
4.如图，图中所有的三角形都是直角三角形，四边形都是正方形.已知正方形A,B,C,D的边长分别是12，16，9，12，求最大正方形E的面积.
解：根据图形正方形E 的边长为:
故E的面积为:252=625.