数学八年级下册第十七章 勾股定理17.1 勾股定理优秀课后练习题

这是一份数学八年级下册第十七章 勾股定理17.1 勾股定理优秀课后练习题，文件包含专题04勾股定理基本应用解析版docx、专题04勾股定理基本应用原卷版docx等2份试卷配套教学资源，其中试卷共31页， 欢迎下载使用。

专题04 勾股定理基本应用
专题说明


勾股定理是人类早期发现并证明的重要数学定理之一，用代数思想解决几何问题的最重要的工具之一。勾股定理揭示了直角三角形三条边之间所存在的数量关系，它只适用于直角三角形，对于锐角三角形和钝角三角形的三边就不具有这一特征。
解题思路


考点1 求线段长
直角三角形两直角边的平方和等于斜边的平方如图：直角三角形ABC的两直角边长分别为，斜边长为，那么.

考点2 求面积
类型一 直角三角形中求斜边上的高
类型二 结合乘法公式巧求面积或长度
类型三 巧妙割补求面积
类型四 “勾股树”及其拓展类型求面积

考点3 解直角三角形
①已知直角三角形的任意两边长，求第三边
在中，，则，，
②知道直角三角形一边，可得另外两边之间的数量关系
③可运用勾股定理解决一些实际问题
【典例分析】
【考点1 求线段长】
【典例1-1】（2022八下·德阳期末）已知△ABC中，BC＝4，AB＝5，∠C＝90°，则AC＝（　　）
A．6 B．41 C．4 D．3
【答案】D
【解答】解：由题可知 ΔABC 为直角三角形，
∴AC=AB2−BC2=52−42=3 ．
故答案为：D.
【典例1-2】（2021八上·龙泉期末）若直角三角形的两边长分别是5和12，则它的斜边长是(　　)
A．13 B．13或 119 C．119 D．12或13
【答案】D
【解答】解：①当12为斜边时，它的斜边长是12；
②当12是直角边时，它的斜边长=122+52=13.
故答案为：D.
【变式1-1】（2021八上·丹东期末）在Rt△ABC中，∠ACB=90°，如果AB=8，BC=6，那么AC的长是（　　）．
A．10 B．27 C．10或27 D．7
【答案】B
【解答】解：∵∠ACB=90°，AB=8，BC=6，
∴AC=AB2−BC2=82−62=27
故答案为：B
【变式1-2】（2021八上·槐荫期末）直角三角形的两直角边长分别为5和12，则斜边长为（　　）
A．13 B．14 C．89 D．1
【答案】A
【解答】解：由题意得，该直角三角形的斜边长为：52+122=13
故答案为：A.
【变式1-3】（2020秋•宝安区期末）若一直角三角形的两边长分别是6，8，则第三边长为（　　）
A．10 B． C．10或 D．14
【答案】C
【解答】解：设第三边为x，
①当8是斜边，则62+x2＝82，
②当8是直角边，则62+82＝x2解得x＝10，
解得x＝2 ．
∴第三边长为10或2．
故选：C．
【考点2 求面积】
【典例2】（2020春•东城区校级期末）若三个正方形的面积如图所示，则正方形A的面积为（　　）

A．6 B．36 C．64 D．8
【答案】B
【解答】解：面积为100的正方形的边长为10，面积为64的正方形的边长为8，
由勾股定理得，正方形A的边长＝＝6，
∴正方形A的面积为36，
故选：B．
【变式2-1】（2021八上·临漳期中）如图所示，在△ABC中，∠ACB＝90°，分别以AB、BC、AC为边向外作正方形，若三个正方形的面积分别为225、400、S，则S的值为（　　）

A．25 B．175 C．600 D．625
【答案】D
【解答】解：在 ΔABC 中， ∠ACB=90° ，
由勾股定理得： AC2+BC2=AB2 ，
∴225+400=S ，
∴S=625 ．
故答案为：D．
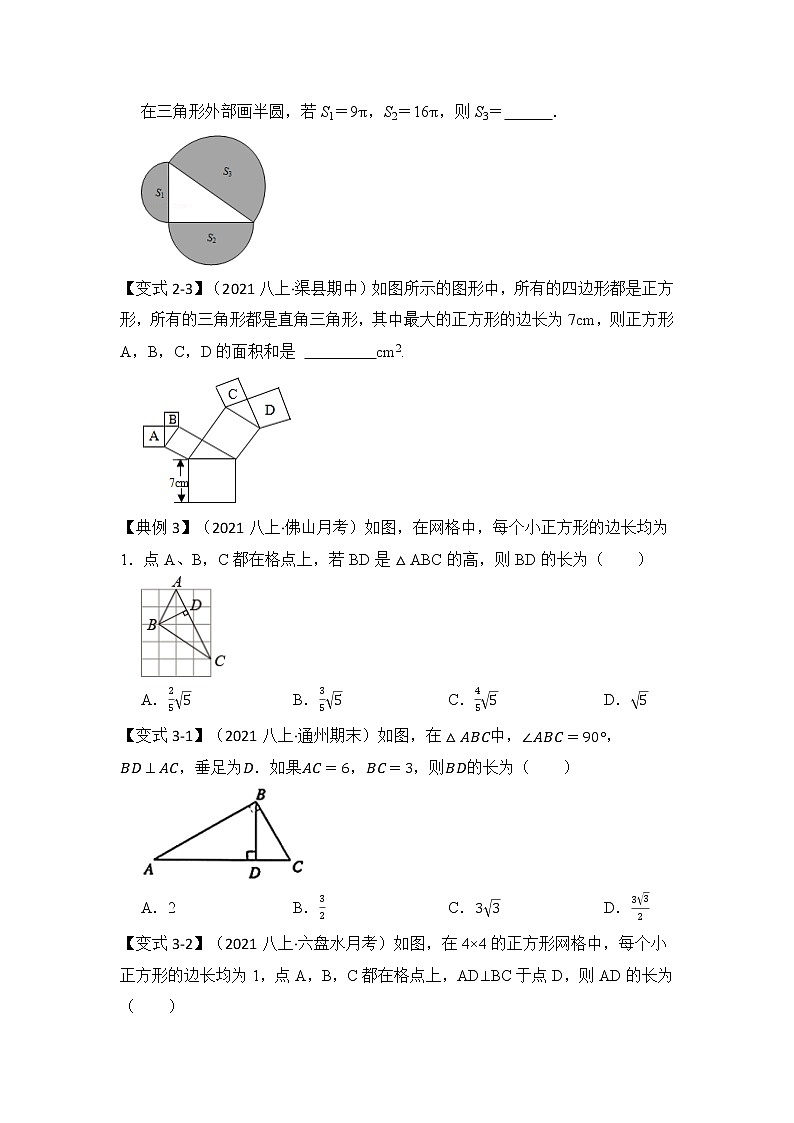
【变式2-2】（2021秋•和平区期末）如图，分别以此直角三角形的三边为直径在三角形外部画半圆，若S1＝9π，S2＝16π，则S3＝　 　．

【答案】25π
【解答】解：设面积为S1的半圆的直径为a，面积为S2的半圆的直径为b，面积为S3的半圆的直径为c，
由勾股定理得：a2+b2＝c2，
由题意得：×π×（）2＝9π，×π×（）2＝16π，
则a2＝72，b2＝128，
∴c2＝200，
∴S3＝×π×（）2＝25π，
故答案为：25π．
【变式2-3】（2021八上·渠县期中）如图所示的图形中，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为7cm，则正方形A，B，C，D的面积和是 　 　cm2.

【答案】49
【解答】解：如图，

设正方形A，B，C，D的边长分别为 a，b，c，d ，设标有 S1，S3 的两个正方形的边长为 x，y ，
根据勾股定理可得 a2+b2=S1=x2，c2+d2=S3=y2
则 x2+y2=S2=72=49
∴a2+b2+c2+d2=49
故答案为：49.
【典例3】（2021八上·佛山月考）如图，在网格中，每个小正方形的边长均为1．点A、B，C都在格点上，若BD是△ABC的高，则BD的长为（　　）

A．255 B．355 C．455 D．5
【答案】C
【解答】解：由题意可得：S△ABC=3×4−2×12−2×42−2×32=4，
∵BD是△ABC的高，AC=22+42=25，
∴S△ABC=BD×252=4，
解得：BD=455，
故答案为：C．
【变式3-1】（2021八上·通州期末）如图，在△ABC中，∠ABC=90°，BD⊥AC，垂足为D．如果AC=6，BC=3，则BD的长为（　　）

A．2 B．32 C．33 D．332
【答案】D
【解答】解：∵∠ABC=90°，AC=6，BC=3，
∴根据勾股定理AB=AC2−BC2=62−32=33，
∵BD⊥AC，
∴S△ABC=12AB⋅BC=12AC⋅BD，即12×33×3=12×6⋅BD，
解得：BD=332．
故答案为：D．
【变式3-2】（2021八上·六盘水月考）如图，在4×4的正方形网格中，每个小正方形的边长均为1，点A，B，C都在格点上，AD⊥BC于点D，则AD的长为（　　）

A．2 B．2 C．5 D．3
【答案】B
【解答】解：由勾股定理得：AB=22+42=25，AC=12+22=5，BC=32+42=5，
∵AB2+AC2＝25，BC2＝25，
∴AB2+AC2＝BC2，
∴∠BAC＝90°，
∴S△ABC=12AC⋅AB=12BC⋅AD，
∴5×25=5×AD，
∴AD＝2，
故答案为：B.

【考点3 解直角三角形】
【典例4】（2021秋•紫金县期中）如图，在△ABC中，∠ADC＝∠BDC＝90°，AC＝20，BC＝15，BD＝9，求AD的长．

【答案】AD=16
【解答】解：在Rt△BDC中，由勾股定理得：
CD＝＝＝12，
在Rt△ACB中，由勾股定理得：
AD＝＝＝16．
【变式4-1】（2021八上·北镇期中）如图，在△ABC中，D是BC边上的一点，若AB＝5，BD＝3，AD＝4，AC＝8，求CD的长．

【解答】解：∵AB＝5，BD＝3，AD＝4，
∴AB2=25，BD2=9，AD2=16 ，
∴AB2=BD2+AD2 ，
∴∠ADB=∠ADC=90° ，
在Rt△ADC中，AC=8，
∴DC=AC2−AD2=43 ．
【变式4-2】（2021八上·连南期中）已知△ABC中，AB＝AC，CD⊥AB于D，若AB＝5，CD＝3，求BC的长．

【解答】解：在Rt△CDA中， ∵AC=AB=5，CD=3，
∴AD= AC2−CD2=4，
∴BD=AB-AD=5-4=1，
在Rt△CBD中，BC= CD2+BD2=12+32=10.


【夯实基础】

1．（2022秋•城关区校级期末）如图，两个较大正方形的面积分别为225，289，则字母A所代表的正方形的面积为（　　）

A．4 B．8 C．16 D．64
【答案】D
【解答】解：∵正方形PQED的面积等于225，
∴即PQ2＝225，
∵正方形PRGF的面积为289，
∴PR2＝289，
又△PQR为直角三角形，根据勾股定理得：
PR2＝PQ2+QR2，
∴QR2＝PR2﹣PQ2＝289﹣225＝64，
则正方形QMNR的面积为64．
故选：D．

2．（2022秋•渝中区校级期末）如图，所有的四边形都是正方形，所有的三角形都是直角三角形，若正方形A、B、C、D的面积分别是6、10、4、6，则最大正方形E的面积是（　　）

A．20 B．26 C．30 D．52
【答案】B
【解答】解：根据勾股定理的几何意义，可得A、B的面积和为S1，C、D的面积和为S2，S1+S2＝S3，

即S3＝6+10+4+6＝26．
故选：B．
3．（2022秋•绥中县校级期末）若直角三角形的两边长分别为a，b，且满足（a﹣3）2+|b﹣4|＝0，则该直角三角形的第三边长的平方为（　　）
A．25 B．7 C．25或7 D．25或16
【答案】C
【解答】解：∵（a﹣3）2+|b﹣4|＝0，
∴a﹣3＝0，b﹣4＝0，
∴a＝3，b＝4，
当b＝4为直角边时，第三边的平方为32+42＝25，
当b＝4为斜边时，第三边的平方为42﹣32＝7，
故选：C．
4．（2022秋•青岛期末）如图，小正方形边长为1，连接小正方形的三个顶点，可得△ABC，则AC边上的高是（　　）

A． B． C． D．
【答案】C
【解答】解：四边形DEFA是正方形，面积是4；
△ABF，△ACD的面积相等，且都是×1×2＝1．
△BCE的面积是：×1×1＝．
则△ABC的面积是：4﹣1﹣1﹣＝．
在直角△ADC中根据勾股定理得到：AC＝＝．
设AC边上的高线长是x．则•AC•x＝x＝，
解得：x＝．
故选：C．

5．（2022春•灵宝市校级月考）如图，以直角三角形的三边a，b，c为边，向外作正方形，等腰直角三角形，等边三角形和半圆，上述四种情况的面积关系满足S1+S2＝S3的图形有（　　）


A．1个 B．2个 C．3个 D．4个
【答案】D
【解答】解：由勾股定理得a2+b2＝c2，
第一个图形中，，，，满足S1+S2＝S3；
第二个图形中，，，，满足S1+S2＝S3；
第三个图形中，，，，满足S1+S2＝S3；
第四个图形中，，，满足S1+S2＝S3；
综上所述，满足题意的图形有4个，
故选：D．
6．（2022春•潜山市月考）如图，点E是正方形ABCD内一点，∠AEB＝90°．若AE＝2，BE＝3，则正方形ABCD的面积为（　　）

A．10 B．13 C．36 D．169
【答案】B
【解答】解：∵∠AEB＝90°，
∴AB2＝AE2+BE2＝22+32＝13，
∴正方形ABCD的面积＝AB2＝13，
故选：B．
7．（2022秋•兴庆区校级月考）如图，△ABC中，∠ABC＝90°，AC＝8，BC＝4，则正方形ABDE的面积为（　　）

A．18 B．48 C．65 D．72
【答案】B
【解答】解：在Rt△ABC中，由勾股定理得，
AB2＝AC2﹣BC2＝82﹣42＝48，
∴正方形ABDE的面积为48，
故选：B．
8．（2022秋•徐汇区期末）一个直角三角形两条直角边的比是3：4，斜边长为10cm，那么这个直角三角形面积为 　 　．
【答案】24cm2
【解答】解：∵一个直角三角形两条直角边的比是3：4，
∴设两条直角边分别为3x，4x，
根据勾股定理得，（3x）2+（4x）2＝102，
∴x＝2，
∴两条直角边分别为6cm和8cm，
∴这个直角三角形面积为×8×6＝24（cm2），
故答案为：24cm2．
9．（2022秋•邢台期末）已知平面直角坐标系中，点P（m﹣2，4）到坐标原点距离为5，则m的值为 　 　．
【答案】5或﹣1．
【解答】解：点P（m﹣2，4）到两坐标轴的距离分别是|m﹣2|、4，
则由勾股定理，得
（m﹣2）2+42＝52，
解得：m＝5或﹣1．
故答案为：5或﹣1．
10．（2022秋•门头沟区期末）已知：如图，在△ABC中，AB＝AC＝5，BC＝8．求BC边上的高的长．

【解答】解：如图，过点A作AD⊥BC于点D，

∵AB＝AC＝5，BC＝8，AD⊥BC，
∴BD＝CD＝BC＝4，
∴AD＝＝＝3，
即BC边上的高的长为3．
11．（2022秋•绿园区校级期末）如图，在△ABC中，∠ACB＝90°，CD⊥AB于点D，AC＝20，BC＝15．
求：（1）CD的长；
（2）AD的长．

【解答】解：（1）在Rt△ABC中，由勾股定理得，
AB＝＝＝25，
∵CD⊥AB，
∴S，
∴CD＝＝12；
（2）在Rt△BDC中，由勾股定理得，
BD＝＝＝9，
AD＝25﹣9＝16．
12．（2022秋•茂南区期末）如图，在由边长为1的小正方形组成的网格中，△ABC的顶点A，B，C恰好在格点（网格线的交点）上．
（1）求△ABC的周长．
（2）求△ABC的面积．

【解答】解：（1）根据题意可得，
AB＝＝＝2，
AC＝＝，
BC＝＝＝5，
AB+AC+BC＝2++5＝5+3，
∴△ABC的周长为5+3；
（2）∵AB＝2，AC＝，BC＝5，
∴BC2＝25，AB2+AC2＝20+5＝25，
∴BC2＝AB2+AC2，
∴△ABC是直角三角形，
∴S△ABC＝AC•AB＝××＝5，
∴△ABC的面积为5．
【能力提升】
13．（2022秋•二七区校级期末）如图，已知直角三角形ABC的周长为24，且阴影部分的面积为24，则斜边AB的长为 　 　．

【答案】10
【解答】解；∵直角三角形ABC的周长为24，
∴AB+AC+BC＝24，AC2+BC2＝AB2，
∴AC2+BC2﹣AB2＝0，
∵阴影部分的面积为24，
∴（）2＝24，
∴+＝24，
∴AC•BC＝48，
∴AC•BC＝＝＝48，
∴AB＝10，
故答案为：10．
14．（2022秋•卧龙区校级期末）对角线互相垂直的四边形叫做“垂美”四边形，现有如图所示的“垂美”四边形ABCD，对角线AC，BD交于点O．若AD＝2，BC＝4，则AB2+CD2＝　 　．

【答案】20
【解答】解：∵AC⊥BD，
∴∠AOD＝∠AOB＝∠BOC＝∠COD＝90°，
由勾股定理得，AB2+CD2＝AO2+BO2+CO2+DO2，
AD2+BC2＝AO2+DO2+BO2+CO2，
∴AB2+CD2＝AD2+BC2，
∵AD＝2，BC＝4，
∴AB2+CD2＝22+42＝20．
故答案为：20．
14．（2022秋•佛山校级期末）如图，在Rt△ABC中，∠C＝90°，AB＝10cm，AC＝6cm，动点P从点B出发沿射线BC以2cm/s的速度移动，设运动的时间为t秒．

（1）求BC边的长；
（2）当△ABP为直角三角形时，求t的值；
（3）当△ABP为等腰三角形时，求t的值．
【解答】解：（1）在Rt△ABC中，BC2＝AB2﹣AC2＝102﹣62＝64，
∴BC＝8（cm）；
（2）由题意知BP＝2tcm，
①当∠APB为直角时，点P与点C重合，BP＝BC＝8cm，即t＝4；
②当∠BAP为直角时，BP＝2tcm，CP＝（2t﹣8）cm，AC＝6cm，
在Rt△ACP中，
AP2＝62+（2t﹣8）2，
在Rt△BAP中，AB2+AP2＝BP2，
即：102+[62+（2t﹣8）2]＝（2t）2，
解得：t＝，
故当△ABP为直角三角形时，t＝4或t＝；
（3）①当AB＝BP时，t＝5；
②当AB＝AP时，BP＝2BC＝16cm，t＝8；
③当BP＝AP时，AP＝BP＝2tcm，CP＝|2t﹣8|cm，AC＝6cm，
在Rt△ACP中，AP2＝AC2+CP2，
所以（2t）2＝62+（2t﹣8）2，
解得：t＝，
综上所述：当△ABP为等腰三角形时，t＝5或t＝8或t＝．


15．（2022秋•二道区校级期末）定义：如图，点M，N把线段AB分割成AM、MN、NB，若以AM，MN，NB为边的三角形是一个直角三角形，则称点M、N是线段AB的勾股分割．

（1）已知M、N把线段AB分割成AM，MN，NB，若AM＝2.5，MN＝6.5，BN＝6，则点M、N是线段AB的勾股分割点吗？请说明理由；
（2）已知点M、N是线段AB的勾股分割点，且AM为直角边，若AB＝30，AM＝5，求BN的长．
【解答】解：（1）点M、N是线段AB的勾股分割点．理由如下：
∵AM2+BN2＝2.52+62＝42.25，MN2＝6.52＝42.25，
∴AM2+NB2＝MN2，
∴AM、MN、NB为边的三角形是一个直角三角形，
∴点M、N是线段AB的勾股分割点；

（2）设BN＝x，则MN＝30﹣AM﹣BN＝25﹣x，
①当MN为最长线段时，依题意MN2＝AM2+NB2，
即（25﹣x）2＝x2+25，
解得x＝12；
②当BN为最长线段时，依题意BN2＝AM2+MN2．
即x2＝25+（25﹣x）2，
解得x＝13．
综上所述，BN＝12或13．
16．（2022秋•通川区校级期末）已知，如图，Rt△ABC中，∠B＝90°，AB＝6，BC＝4，以斜边AC为底边作等腰三角形ACD，腰AD刚好满足AD∥BC，并作腰上的高AE．
（1）求证：AB＝AE；
（2）求等腰三角形的腰长CD．

【解答】（1）证明：∵DA＝DC，
∴∠DAC＝∠DCA，
∵AD∥BC，
∴∠DAC＝∠BCA，
∴∠ACB＝∠DCA，
又∵AE⊥CD，
∴∠AEC＝90°，
∴∠A＝∠AEC＝90°，
在△ABC和△AEC中，，
∴△ABC≌△AEC（AAS），
∴AB＝AE；
（2）解：由（1）得：AE＝AB＝6，CE＝CB＝4，
设DC＝x，则DA＝x，DE＝x﹣4，
由勾股定理得：DE2+AE2＝DA2，
即（x﹣4）2+62＝x2，
解得：x＝，
即CD＝．