初中数学人教版八年级下册17.1 勾股定理课时练习

《17.1勾股定理》课后专题练习

一、单选题

1、如图，A（8，0），B（0，6），以点A为圆心，AC长为半径画弧，交y轴正半轴于点B，则点C的坐标为（    ）

A．（10，0） B．（0，10） C．（-2，0） D．（0，-2）

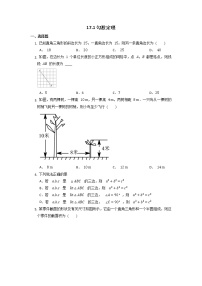
2、如图，在3×3的网格中，每个小正方形的边长均为1，点A，B，C都在格点上，若BD是△ABC的高，则BD的长为（　　）

A． B． C． D．

3、如图，在ABC中，∠B＝22.5°，∠C＝45°，若AC＝2，则ABC的面积是（    ）

A． B．1+ C．2 D．2+

4、如图，我国古代的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺构成的大正方形，若小正方形的面积为1，大正方形的面积为13，则直角三角形较短的直角边a与较长的直角边b的比的值是（　　）

A． B． C． D．

5、勾股定理是人类最伟大的科学发现之一，在我国古算书《周髀算经》中早有记载．如图1，以直角三角形的各边为边分别向外作正方形，再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积，则一定能求出（    ）

A．直角三角形的面积

B．最大正方形的面积

C．较小两个正方形重叠部分的面积

D．最大正方形与直角三角形的面积和

6．如图，在△ABC中，∠C＝90°，AD平分∠BAC交BC于点D．若BC＝16，且CD：BD＝3：5，则点D到边AB的距离为（　　）

A．3 B．5 C．6 D．10

7．在Rt△ABC中，∠ABC＝90°，AC＝13，AB＝12，则图中五个小直角三角形的周长之和为（　　）

A．25 B．18 C．17 D．30

8．如图，在△ABC中，∠ACB＝90°，BC＝8cm，以点A为圆心，AC长为半径画弧，交线段AB于点D；以B为圆心，BD长为半径画弧，交线段BC于点E．若BD＝CE，则AC的长为（　　）

A．6cm B．6.5cm C．7cm D．7.5cm

二、填空题

1、《九章算术》中有“折竹抵地”问题：“今有竹高一丈，末折抵地，去根三尺，问折者高几何？”题意是：有一根竹子原来高1丈（1丈=10尺），中部有一处折断，竹梢触地面处离竹根3尺，试问折断处离地面多高？如图，设折断处距离地面x尺，根据题意，可列方程为______．

2、如图，AB⊥BC，CD⊥BC，垂足分别为B，C，P为线段BC上一点，连结PA，PD．已知AB＝5，DC＝4，BC＝12，则AP+DP的最小值为_____．

3、某小区两面直立的墙壁之间为安全通道，一架梯子斜靠在左墙DE时，梯子A到左墙的距离AE为0.7m，梯子顶端D到地面的是样子离DE为2.4m，若梯子底端A保持不动，将梯子斜塞在右墙BC上，梯子顶端C到地面的距离CB为1.5m，则这两面直立墙壁之间的安全道的宽BE为__________m．

4、如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，AD是∠BAC的平分线，若P，Q分别是AD和AC上的动点，则PC+PQ的最小值是______．

5、如图，有一直角三角形纸片，边，，，将该直角三角形纸片沿折叠，使点与点重合，则四边形的周长为______.

三、解答题

1、如图是规格为8×8的正方形网格，每个小正方形的边长均为1，请在所给网格中按下列要求操作：

(1)在网格中建立平面直角坐标系，使A点坐标为（4，2），B点坐标为（1，-1）；

(2)在第一象限内的格点上画一点C，使点C与线段AB构成一个以AB为底的等腰三角形，且腰长是无理数，则C点坐标是　　；

(3)△ABC的周长=　　　；（结果保留根号）

(4)若△A'B'C'与△ABC关于y轴对称，写出点A'和点B'的坐标．

2．长清的园博园广场视野开阔，阻挡物少，成为不少市民放风筝的最佳场所，某校七年级（1）班的小明和小亮学习了“勾股定理”之后，为了测得风筝的垂直高度CE，他们进行了如下操作：①测得水平距离BD的长为15米；②根据手中剩余线的长度计算出风筝线BC的长为25米；③牵线放风筝的小明的身高为1.6米．

(1)求风筝的垂直高度CE；

(2)如果小明想风筝沿CD方向下降12米，则他应该往回收线多少米？

3．小王与小林进行遥控赛车游戏，终点为点，小王的赛车从点出发，以米/秒的速度由西向东行驶，同时小林的赛车从点出发，以米/秒的速度由南向北行驶（如图）．已知赛车之间的距离小于或等于米时，遥控信号会产生相互干扰，米，米，

（1）出发秒钟时，遥控信号是否会产生相互干扰？

（2）当两赛车距点的距离之和为米时，遥控信号是否会产生相互干扰？

4．如图，在△ABC和△DCE中，AC＝DE，∠B＝∠DCE＝90°，点A，C，D依次在同一直线上，且AB∥DE．

（1）求证：△ABC≌△DCE；

（2）连结AE，当BC＝5，AC＝12时，求AE的长．

5、如图，在△ABC中，∠B＝45°，∠C＝30°，边AC的垂直平分线分别交边BC、AC于点D、E，DC＝6．求AB的长．

6、已知：如图，在中，，为的中点，、分别在、上，且于.求证：.