资料中包含下列文件,点击文件名可预览资料内容









还剩12页未读,
继续阅读
所属成套资源:北京课改版数学八年级下册课件PPT(送教学设计)全册
成套系列资料,整套一键下载
- 14.7一次函数的应用 课件+教案 课件 4 次下载
- 15.1四边形 课件+教案 课件 3 次下载
- 15.3四边形 课件+(3课时)教案 课件 3 次下载
- 15.4四边形 课件+(2课时)教案 课件 3 次下载
- 15.5四边形 课件+(3课时)教案 课件 3 次下载
15.2四边形 课件+(3课时)教案
展开
这是一份15.2四边形 课件+(3课时)教案
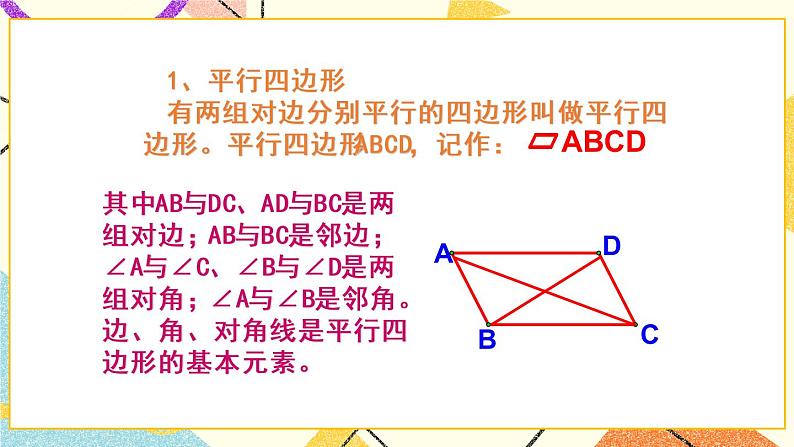
15章 四边形15.2平行四边形及特殊平行四边形1、平行四边形有两组对边分别平行的四边形叫做平行四边形。平行四边形ABCD,记作:其中AB与DC、AD与BC是两组对边;AB与BC是邻边;∠A与∠C、∠B与∠D是两组对角;∠A与∠B是邻角。边、角、对角线是平行四边形的基本元素。(1)从边的关系去判定 ①一组对边平行且相等的四边形是平行四边形。 ②两组对边分别平行的四边形是平行四边形。 ③两组对边分别相等的四边形是平行四边形。(2)从角的关系去判定 ④两组对角分别相等的四边形是平行四边 (注:邻角都互补的四边形是平行四边形。)(3)从对角线的关系去判定: ⑤对角线相互平分的四边形是平行四边形。平行四边形的判定识别(1)从边的关系分析 ①平行四边形对边平行且相等。(2)从角的关系分析 ②平行四边形对角相等、邻角互补。(3)从对角线分析 ③平行四边形对角线互相平分。(4)从对称性分析 ④平行四边形是中心对称图形,对角线交点是对称中心。(注:由中心对称性,可通过绕三角形一边中点旋转180°来构造平行四边形。) 平行四边形的性质特征2、矩形:有一个角是90°的平行四边形叫矩形矩形的判定定理:(1)有一个角是直角的平行四边形是矩形。(2)有三个角是直角的四边形是矩形。(3)对角线相等的平行四边形是矩形。(4)对角线相等且相互平分的四边形是矩形。矩形的性质定理:(1)矩形的四个角都是直角。(2)矩形的对角线相等且相互平分。(3)矩形既是轴对称图形,又是中心对称图形。 3、菱形:四条边都相等的四边形叫菱形。菱形的判定定理:①四条边都相等的四边形是菱形。②有一组邻边相等的平行四边形是菱形。 ③对角线互相垂直的平行四边形是菱形。④对角线互相垂直且平分的四边形是菱形。菱形的性质定理:①菱形四条边都相等。②菱形对角线互相垂直且平分,并且每条对角线 平分一组对角。③菱形既是轴对称图形又是中心对称图形。④菱形面积等于它的两条对角线的乘积的一半。4、正方形:四个角都是直角,四条边都相等的四边形。正方形的判定定理:(1)有一组邻边相等的矩形是正方形。(2)对角线相互垂直的矩形是正方形。(3)有一个角是直角的菱形是正方形。(4)对角线相等的菱形是正方形。(5)对角线互相垂直平分且相等的四边形是 正方形。 注:证明四边形是正方形往往先证明它是矩形或菱形,然后再证明其是正方形,有时也从对角线关系出发直接证其是正方形。正方形的性质:(1)正方形的四个角都是直角,四条边 都相等。(2)正方形的两对角线互相垂直平分且 相等,并且每条对角线平分一组对角。(3)正方形既是中心对称图形,又是轴对称 图形。(4)正方形的边长与对角线长的比为 。图形解读四边形内在联系1、利用平行四边形定义、性质来判定 线段相等或平行;两角相等或互补。特殊四边形的性质特点的实战应用2、利用矩形特殊性质来判定90°的角。3、利用菱形、正方形特征判定线段相等; 线段相互垂直平分等。4、利用性质来进行有关线段、角和面积 的计算。 例1:如图所示,平行四边形ABCD中,点E、F在对角线AC上,且AE=CF。求证:四边形BEDF是平行四边形。证明:连结BD,交AC于点O。 在平行四边形ABCD中 则 ∴四边形BFDE为 平行四边形。 方法较多时,尽量考虑简单办法。例2:分别以平行四边形ABCD的邻边AB和AD为一边,在平行四边形ABCD外作正三角形ABF和正三角形ADE,连结CE、EF、CF得△CEF,试判断△CEF的形状,并证明你的结论。证明:∵四边形ABCD是平行四边形∵△ADE、△ABF为正三角形 CECF等边例3:如图所示,延长矩形的边CB至E,使CE=CA, F是AE的中点,求证: 。 证明:连接CF, ∵四边形ABCD是矩形 ∵F是AE的中点 在△ADF和△BCF中 例4:如图所示,E、F分别在正方形ABCD的边BC、CD上,且 ,求证:EF=BE+DF。 12 证明:将△ADF旋转至△ABG,则 例5:如图所示,将矩形ABCD沿着直线BD折叠,使 点C落在C’处,BC’交AD于E,AD=8,AB=4, 求:△BED的面积。F123 解:在矩形ABCD中,AD//BC,因:矩形ABCD沿直线BD折叠后,△BC’D与△BCD关于直线BD对称 123xxF1、熟知平行四边形及特殊平行四边形的性质及判定;2、知道以上性质、判定的作用,并能够在需要时准确选择应用;3、相关知识(如:勾股定理、旋转、折叠、直角三角形中相关特性等)的应用反映及时、准确。当 堂 小 结多练、多见到熟练,仔细分析不怕难!祝大家学习愉快!BYE BYE
15章 四边形15.2平行四边形及特殊平行四边形1、平行四边形有两组对边分别平行的四边形叫做平行四边形。平行四边形ABCD,记作:其中AB与DC、AD与BC是两组对边;AB与BC是邻边;∠A与∠C、∠B与∠D是两组对角;∠A与∠B是邻角。边、角、对角线是平行四边形的基本元素。(1)从边的关系去判定 ①一组对边平行且相等的四边形是平行四边形。 ②两组对边分别平行的四边形是平行四边形。 ③两组对边分别相等的四边形是平行四边形。(2)从角的关系去判定 ④两组对角分别相等的四边形是平行四边 (注:邻角都互补的四边形是平行四边形。)(3)从对角线的关系去判定: ⑤对角线相互平分的四边形是平行四边形。平行四边形的判定识别(1)从边的关系分析 ①平行四边形对边平行且相等。(2)从角的关系分析 ②平行四边形对角相等、邻角互补。(3)从对角线分析 ③平行四边形对角线互相平分。(4)从对称性分析 ④平行四边形是中心对称图形,对角线交点是对称中心。(注:由中心对称性,可通过绕三角形一边中点旋转180°来构造平行四边形。) 平行四边形的性质特征2、矩形:有一个角是90°的平行四边形叫矩形矩形的判定定理:(1)有一个角是直角的平行四边形是矩形。(2)有三个角是直角的四边形是矩形。(3)对角线相等的平行四边形是矩形。(4)对角线相等且相互平分的四边形是矩形。矩形的性质定理:(1)矩形的四个角都是直角。(2)矩形的对角线相等且相互平分。(3)矩形既是轴对称图形,又是中心对称图形。 3、菱形:四条边都相等的四边形叫菱形。菱形的判定定理:①四条边都相等的四边形是菱形。②有一组邻边相等的平行四边形是菱形。 ③对角线互相垂直的平行四边形是菱形。④对角线互相垂直且平分的四边形是菱形。菱形的性质定理:①菱形四条边都相等。②菱形对角线互相垂直且平分,并且每条对角线 平分一组对角。③菱形既是轴对称图形又是中心对称图形。④菱形面积等于它的两条对角线的乘积的一半。4、正方形:四个角都是直角,四条边都相等的四边形。正方形的判定定理:(1)有一组邻边相等的矩形是正方形。(2)对角线相互垂直的矩形是正方形。(3)有一个角是直角的菱形是正方形。(4)对角线相等的菱形是正方形。(5)对角线互相垂直平分且相等的四边形是 正方形。 注:证明四边形是正方形往往先证明它是矩形或菱形,然后再证明其是正方形,有时也从对角线关系出发直接证其是正方形。正方形的性质:(1)正方形的四个角都是直角,四条边 都相等。(2)正方形的两对角线互相垂直平分且 相等,并且每条对角线平分一组对角。(3)正方形既是中心对称图形,又是轴对称 图形。(4)正方形的边长与对角线长的比为 。图形解读四边形内在联系1、利用平行四边形定义、性质来判定 线段相等或平行;两角相等或互补。特殊四边形的性质特点的实战应用2、利用矩形特殊性质来判定90°的角。3、利用菱形、正方形特征判定线段相等; 线段相互垂直平分等。4、利用性质来进行有关线段、角和面积 的计算。 例1:如图所示,平行四边形ABCD中,点E、F在对角线AC上,且AE=CF。求证:四边形BEDF是平行四边形。证明:连结BD,交AC于点O。 在平行四边形ABCD中 则 ∴四边形BFDE为 平行四边形。 方法较多时,尽量考虑简单办法。例2:分别以平行四边形ABCD的邻边AB和AD为一边,在平行四边形ABCD外作正三角形ABF和正三角形ADE,连结CE、EF、CF得△CEF,试判断△CEF的形状,并证明你的结论。证明:∵四边形ABCD是平行四边形∵△ADE、△ABF为正三角形 CECF等边例3:如图所示,延长矩形的边CB至E,使CE=CA, F是AE的中点,求证: 。 证明:连接CF, ∵四边形ABCD是矩形 ∵F是AE的中点 在△ADF和△BCF中 例4:如图所示,E、F分别在正方形ABCD的边BC、CD上,且 ,求证:EF=BE+DF。 12 证明:将△ADF旋转至△ABG,则 例5:如图所示,将矩形ABCD沿着直线BD折叠,使 点C落在C’处,BC’交AD于E,AD=8,AB=4, 求:△BED的面积。F123 解:在矩形ABCD中,AD//BC,因:矩形ABCD沿直线BD折叠后,△BC’D与△BCD关于直线BD对称 123xxF1、熟知平行四边形及特殊平行四边形的性质及判定;2、知道以上性质、判定的作用,并能够在需要时准确选择应用;3、相关知识(如:勾股定理、旋转、折叠、直角三角形中相关特性等)的应用反映及时、准确。当 堂 小 结多练、多见到熟练,仔细分析不怕难!祝大家学习愉快!BYE BYE
相关资料
更多









