

北京市海淀区2022-2023学年七年级上册数学期末专项提升试题(卷一卷二)含解析
展开北京市海淀区2022-2023学年七年级上册数学期末专项提升试题(卷一)
一、选一选(每小题4分,共48分)
1. 的相反数是( )
A. B. C. D.
2. 某地的气温是8℃,气温是-2℃,则该地这天的温差是( )
A. -10℃ B. 10℃ C. 6℃ D. -6℃
3. 我国于2016年9月15日成功发射天宫二号空间实验室.它是我国自主研发的第二个空间实验室,标志着我国即将迈入空间站时代.天宫二号空间实验室运行的轨道高度距离地球393000日,数据393000用科学记数法表示为( )
A. 3.93×106 B. 39.3×104 C. 0.393×106 D. 3.93×105
4. 下列计算正确的是( )
A. B.
C. 3x﹣2x=1 D.
5. 如果-2amb2与a5bn+1的和仍然是单项式,那么m+n的值为( ).
A. 5 B. 6 C. 7 D. 8
6. 把下列图标折成一个正方体的盒子,折好后与“中”相对的字是( )
A. 祝 B. 你 C. 顺 D. 利
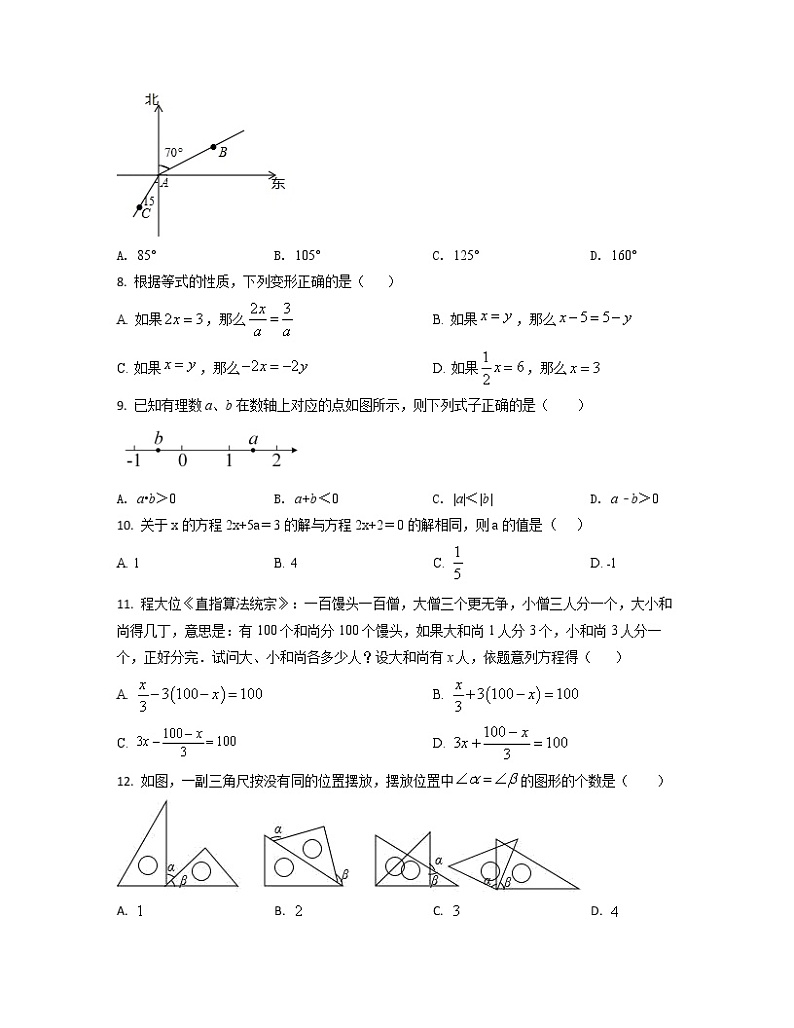
7. 如图,甲从A点出发向北偏东70°方向走到点B,乙从点A出发向南偏西15°方向走到点C,则∠BAC的度数是( )
A. 85° B. 105° C. 125° D. 160°
8. 根据等式的性质,下列变形正确的是( )
A. 如果,那么 B. 如果,那么
C. 如果,那么 D. 如果,那么
9. 已知有理数a、b在数轴上对应的点如图所示,则下列式子正确的是( )
A. a•b>0 B. a+b<0 C. |a|<|b| D. a﹣b>0
10. 关于x的方程2x+5a=3的解与方程2x+2=0的解相同,则a的值是( )
A. 1 B. 4 C. D. ﹣1
11. 程大位《直指算法统宗》:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚得几丁,意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分一个,正好分完.试问大、小和尚各多少人?设大和尚有x人,依题意列方程得( )
A. B.
C. D.
12. 如图,一副三角尺按没有同的位置摆放,摆放位置中的图形的个数是( )
A. B. C. D.
二、填 空 题(每小题4分,共24分)
13. 比较大小:______.
14. 如图,从地到地共有五条路,人们常常选择第③条,请用几何知识解释原因____.
15. 57.32° = _______( )' ______ "
16. 互联网“”经营已成为大众创业新途径.某平台上一件商品进价为180元,按标价的八折,仍可获利60元,求这件商品的标价为________.
17. 如图,是线段上一点,M是线段中点,N是线段BC的中点且MN=3cm,则的长为cm.
18. 下列图案是我国古代窗格的一部分,其中“○”代表窗纸上所贴的剪纸,则第5个图中所贴剪纸“○”的个数为__________ ,第个图中所贴剪纸“○”的个数为__________.
三、解 答 题(共78分)
19. 计算:
(1);
(2)﹣110﹣8÷(﹣2)+4×|﹣5|.
20. 解方程:
(1) (2)
21. 先化简,再求值
,其中.
22. 如图,平面上有四个点A,B,C,D.
(1)根据下列语句画图:
①射线BA;
②直线AD,BC相交于点E;
③延长DC至F(虚线),使CF=BC,连接EF(虚线).
(2)图中以E为顶点的角中,小于平角的角共有__________个.
23. 如图①,将笔记本活页一角折过去,使角的顶点A落在处,BC为折痕.
(1)图①中,若∠1=30°,求∠度数;
(2)如果又将活页的另一角斜折过去,使BD边与BA重合,折痕为BE,如图②所示,∠1=30°,求∠2以及∠的度数;
(3)如果在图②中改变∠1的大小,则的位置也随之改变,那么问题(2)中∠的大小是否改变?请说明理由.
24. 八达岭森林体验,由八达岭森林体验馆和450公顷的户外体验区构成.森林体验馆包括“八达岭森林变迁“、“八达岭森林大家族“、“森林让生活更美好“等展厅,户外游憩体验系统根据森林生态旅游理念,采取少设施、设施集中的点线布局模式,突破传统的“看风景“旅游模式,强调全面体验森林之美.
在室内展厅内,有这样一个可以动手操作体验的仪器,如图,小明在社会大课堂中,记录了这样一组数字:
交通
工具
行驶100公里的碳足迹(kg)
100公里碳中
和树木棵树
飞机
13.9
0.06
小轿车
22.5
0.10
公共汽车
13
0005
根据以上材料回答问题:
A,B两地相距300公里,小轿车以90公里/小时的速度从A地开往B地;公共汽车以60公里/小时的速度从B开往A地,两车同时出发相对而行,两车在C地相遇,相遇后继续前行到达各自的目的地.
(1)多少小时后两车相遇?
(2)小轿车和公共汽车分别到达目的地,计算小轿车的碳足迹为多少?公共汽车的碳中和树木棵数为多少?
(3)根据观察或计算说明,为了减少环境污染,我们应该选择哪种交通工具出行更有利于环保呢?
25. 我们已经学习了“乘方”运算,下面介绍一种新运算,即“对数”运算.
定义:如果(a>0,a≠1,N>0),那么b叫做以a为底N的对数,记作.
例如:因,所以;因为,所以.
根据“对数”运算的定义,回答下列问题:
(1)填空: , .
(2)如果,求m的值.
(3)对于“对数”运算,小明同学认为有“(a>0,a≠1,M>0,N>0)”,他的说确吗?如果正确,请给出证明过程;如果没有正确,请说明理由,并加以改正.
北京市海淀区2022-2023学年七年级上册数学期末专项提升试题(卷一)
一、选一选(每小题4分,共48分)
1. 的相反数是( )
A. B. C. D.
【正确答案】B
【详解】解:-8的相反数是8.故选B.
2. 某地的气温是8℃,气温是-2℃,则该地这天的温差是( )
A. -10℃ B. 10℃ C. 6℃ D. -6℃
【正确答案】B
【详解】试题分析:根据题意算式,计算即可得到结果.
根据题意得:8﹣(﹣2)=8+2=10,则该地这天的温差是10℃,
故选:B.
考点:有理数的减法
3. 我国于2016年9月15日成功发射天宫二号空间实验室.它是我国自主研发的第二个空间实验室,标志着我国即将迈入空间站时代.天宫二号空间实验室运行的轨道高度距离地球393000日,数据393000用科学记数法表示为( )
A 3.93×106 B. 39.3×104 C. 0.393×106 D. 3.93×105
【正确答案】D
【详解】解:393 000=3.93×105.
故选D.
科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值是易错点,由于393000有6位,所以可以确定n=6-1=5.
4. 下列计算正确的是( )
A. B.
C. 3x﹣2x=1 D.
【正确答案】D
【分析】根据合并同类项的法则:系数相加字母部分没有变,可得答案.
【详解】A.,错误;
B.原式没有能合并,错误;
C.3x﹣2x=x,错误;
D.,正确.
故选:D.
5. 如果-2amb2与a5bn+1的和仍然是单项式,那么m+n的值为( ).
A. 5 B. 6 C. 7 D. 8
【正确答案】B
【分析】所含字母相同,并且相同字母的指数也相同,这样的项叫做同类项.
【详解】解:∵-2amb2与a5bn+1是同类项,
∴m=5,n+1=2,
解得:m=1,
∴m+n=6.
故选B.
本题主要考查的是同类项的定义,熟练掌握同类项的定义是解题的关键.
6. 把下列图标折成一个正方体的盒子,折好后与“中”相对的字是( )
A. 祝 B. 你 C. 顺 D. 利
【正确答案】C
【分析】利用正方体及其表面展开图的特点解题.
【详解】解:这是一个正方体的平面展开图,共有六个面,其中面“祝”与面“利”相对,面“你”与面“考”相对,面“中”与面“顺”相对.
故选:C.
本题考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.
7. 如图,甲从A点出发向北偏东70°方向走到点B,乙从点A出发向南偏西15°方向走到点C,则∠BAC的度数是( )
A. 85° B. 105° C. 125° D. 160°
【正确答案】C
【分析】首先求得AB与正东方向的夹角的度数,即可求解.
【详解】根据题意得:∠BAC=(90°﹣70°)+15°+90°=125°,
故选:C.
本题考查了方向角,正确理解方向角的定义是关键.
8. 根据等式性质,下列变形正确的是( )
A. 如果,那么 B. 如果,那么
C. 如果,那么 D. 如果,那么
【正确答案】C
【分析】根据等式的基本性质解决此题.
【详解】解:A、如果,且a,那么,故该选项没有符合题意;
B、如果,那么,故该选项没有符合题意;
C、如果,那么,故该选项符合题意;
D、如果,那么,故该选项没有符合题意;
故选:C.
本题主要考查等式的基本性质,熟练掌握等式的基本性质是解决本题的关键.
性质1、等式两边加同一个数(或式子)结果仍得等式;
性质2、等式两边乘同一个数或除以一个没有为零的数,结果仍得等式.
9. 已知有理数a、b在数轴上对应的点如图所示,则下列式子正确的是( )
A. a•b>0 B. a+b<0 C. |a|<|b| D. a﹣b>0
【正确答案】D
【详解】试题解析:由数轴可知:
A. 故错误.
B.故错误.
C.故错误.
D.正确.
故选:D.
10. 关于x的方程2x+5a=3的解与方程2x+2=0的解相同,则a的值是( )
A 1 B. 4 C. D. ﹣1
【正确答案】A
【详解】根据方程的解相同,可得关于a的方程,解方程即可得答案.
解:解方程,得
把代入得,
,
解得
故选A.
11. 程大位《直指算法统宗》:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚得几丁,意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分一个,正好分完.试问大、小和尚各多少人?设大和尚有x人,依题意列方程得( )
A. B.
C. D.
【正确答案】D
【分析】根据100个和尚分100个馒头,正好分完.大和尚一人分3个,小和尚3人分一个得到等量关系为:大和尚的人数+小和尚的人数=100,大和尚分得的馒头数+小和尚分得的馒头数=100,依此列出方程即可.
【详解】解:设大和尚有x人,则小和尚有(100-x)人,
根据题意得:;
故选:D.
本题考查了由实际问题抽象出一元方程,关键以和尚数和馒头数作为等量关系列出方程.
12. 如图,一副三角尺按没有同的位置摆放,摆放位置中的图形的个数是( )
A. B. C. D.
【正确答案】C
【分析】根据直角三角板可得个图形∠β=45°,进而可得∠α=45°;根据余角和补角的性质可得第二个图形、第四个图形中∠α=∠β,第三个图形∠α和∠β互补.
【详解】根据角的和差关系可得个图形∠α=∠β=45°,
根据等角的补角相等可得第二个图形∠α=∠β,
第三个图形∠α+∠β=180°,没有相等,
根据同角的余角相等可得第四个图形∠α=∠β,
因此∠α=∠β的图形个数共有3个,
故选:C.
此题主要考查了余角和补角,关键是掌握余角和补角的性质:等角的补角相等.等角的余角相等.
二、填 空 题(每小题4分,共24分)
13. 比较大小:______.
【正确答案】>
【分析】先将两个分数通分,然后进行比较即可.
【详解】解:=,=,
∵>,
∴>,
故>.
本题考查了分数的大小比较,掌握知识点是解题关键.
14. 如图,从地到地共有五条路,人们常常选择第③条,请用几何知识解释原因____.
【正确答案】两点之间,线段最短
【详解】试题分析:在连接A、B的所有连线中,③是线段,是最短的,所以选择③的原因是:两点之间,选段最短.
故答案为两点之间,线段最短.
15. 57.32° = _______( )' ______ "
【正确答案】 ①. 57 ②. 19 ③. 12
【详解】解:57.32°=57°19′12″.故答案为57,19,12.
16. 互联网“”经营已成为大众创业新途径.某平台上一件商品进价为180元,按标价的八折,仍可获利60元,求这件商品的标价为________.
【正确答案】300元
【详解】解:设这件商品的标价为x元,
根据题意得:0.8x﹣180=60,
解得:x=300.
故300元.
17. 如图,是线段上一点,M是线段的中点,N是线段BC的中点且MN=3cm,则的长为cm.
【正确答案】6
【详解】解:∵M是线段AC的中点,N是线段BC的中点,∴AC=2MC,BC=2CN,∴AB=AC+BC=2(MC+CN)=2MN=6cm.故答案为6.
18. 下列图案是我国古代窗格的一部分,其中“○”代表窗纸上所贴的剪纸,则第5个图中所贴剪纸“○”的个数为__________ ,第个图中所贴剪纸“○”的个数为__________.
【正确答案】 ①. 17, ②. 3n+2
【详解】解:个图案为3+2=5个窗花;
第二个图案为2×3+2=8个窗花;
第三个图案为3×3+2=11个窗花;
…从而可以探究:
第n个图案所贴窗花数为(3n+2)个,当n=5时,3n+2=3×5+2=17个.
故答案为17,3n+2.
点睛:考查了规律型:图形的变化,本题是一道找规律的题目,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.
三、解 答 题(共78分)
19. 计算:
(1);
(2)﹣110﹣8÷(﹣2)+4×|﹣5|.
【正确答案】(1)24;(2)23
【详解】试题分析:(1)括号内分母6,4,12都是48的因数,所以可以使用乘法的分配率简化运算;
(2)先计算乘方和化简值,然后计算除法和乘法,计算加减即可.
试题解析:
解:(1)原式=
=-8+36-4
=24;
(2)原式=-1-8÷(-2)+4×5
=-1+4+20
=23.
点睛:本题考查是有理数的运算能力.注意:要正确掌握运算顺序,即乘方运算(和以后学习的开方运算)叫做三级运算;乘法和除法叫做二级运算;加法和减法叫做一级运算.在混合运算中要特别注意运算顺序:先三级,后二级,再一级;有括号的先算括号里面的;同级运算按从左到右的顺序.注意恰当的使用运算律可以简化运算.
20. 解方程:
(1) (2)
【正确答案】(1)x=1; (2)x=.
【详解】试题分析:(1)先去括号,然后把未知项移至等号左边,常数项移至等号右边,再合并同类项,两边除以未知数的系数,把系数化为1即可;
(2)两边乘以6去掉分母,然后去括号,移项,合并同类项,系数化为1即可.
试题解析:
解:(1)2x-6=2(3x-5),
去括号得:2x-6=6x-10,
移项得:2x-6x=-10+6,
合并同类项得:-4x=-4,
系数化为1得:x=1;
(2)去分母得:3(x+1)-6=2(2-x),
去括号得:3x+3-6=4-2x,
移项得:3x+2x=4-3+6,
合并同类项得:5x=7,
系数化为1得:x=.
点睛:本题考查了一元方程的解法,熟记解法的一般步骤和等式的性质是解决此题的关键.
21. 先化简,再求值
,其中.
【正确答案】化简结果:,原式=-7
【详解】试题分析:先根据两个非负数的和为0则这两个数都为0求出x、y的值,然后先去掉小括号,再去掉中括号,合并同类项后,代入x、y的值计算即可.
试题解析:
解:∵|x+1|+(y-2)2=0,
∴x+1=0,y-2=0,
解得:x=-1,y=2,
4x2 y-[6xy-3(4xy-2)-x2y]+1
=4x2 y-[6xy-12xy+6-x2y]+1
=4x2 y-6xy+12xy-6+x2y+1
=5x2 y+6xy-5,
当x=-1,y=2时,
原式=5×(-1)2×2+6×(-1)×2-5
=10-12-5
=-7.
22. 如图,平面上有四个点A,B,C,D.
(1)根据下列语句画图:
①射线BA;
②直线AD,BC相交于点E;
③延长DC至F(虚线),使CF=BC,连接EF(虚线).
(2)图中以E为顶点的角中,小于平角的角共有__________个.
【正确答案】(1)见解析;(2)8
【分析】(1) 根据直线、射线、线段的特点画出图形即可;
(2)有公共端点的两条射线组成的图形叫做角,根据角的概念数出角的个数即可.
【详解】解:(1)画图如下:
(2)(前面数过的没有再重数)以EF为始边的角有4个,以EC为始边的角有1个,以EA为始边的角有1个,以EC的反向延长线为始边的有1个,以EA的反向延长线为始边的有1个,所以以E为顶点的角中,小于平角的角共有8个.
此题主要考查了角、直线、射线、线段,关键是掌握角的概念及直线、射线、线段的特点.
23. 如图①,将笔记本活页一角折过去,使角的顶点A落在处,BC为折痕.
(1)图①中,若∠1=30°,求∠的度数;
(2)如果又将活页的另一角斜折过去,使BD边与BA重合,折痕为BE,如图②所示,∠1=30°,求∠2以及∠的度数;
(3)如果在图②中改变∠1的大小,则的位置也随之改变,那么问题(2)中∠的大小是否改变?请说明理由.
【正确答案】(1)120°;(2)90°.(3)结论:∠CBE没有变.
【分析】(1)先根据折叠的性质求出∠ABC的度数,然后根据∠A′BD=180°-∠ABC-∠1计算即可;
(2)由∠A′BD=120°,∠2=∠DBE,可得∠2=∠A′BD=60°,根据∠CBE=∠1+∠2计算出∠CBE;
(3)由∠1+∠2=∠ABA′+∠A′BD=(∠ABA′+∠A′BD)计算即可.
【详解】解:(1)∵∠1=30°,
∴∠1=∠ABC=30°,
∴∠A′BD=180°-30°-30°=120°.
(2)∵∠A′BD=120°,∠2=∠DBE,
∴∠2=∠A′BD=60°,
∴∠CBE=∠1+∠2=30°+60°=90°.
(3)结论:∠CBE没有变.
∵∠1=∠ABA′,∠2=∠A′BD,∠ABA′+∠A′BD=180°,
∴∠1+∠2=∠ABA′+∠A′BD
=(∠ABA′+∠A′BD)
=×180°
=90°.
即∠CBE=90°.
24. 八达岭森林体验,由八达岭森林体验馆和450公顷的户外体验区构成.森林体验馆包括“八达岭森林变迁“、“八达岭森林大家族“、“森林让生活更美好“等展厅,户外游憩体验系统根据森林生态旅游理念,采取少设施、设施集中的点线布局模式,突破传统的“看风景“旅游模式,强调全面体验森林之美.
在室内展厅内,有这样一个可以动手操作体验的仪器,如图,小明在社会大课堂中,记录了这样一组数字:
交通
工具
行驶100公里的碳足迹(kg)
100公里碳中
和树木棵树
飞机
13.9
0.06
小轿车
22.5
0.10
公共汽车
1.3
0.005
根据以上材料回答问题:
A,B两地相距300公里,小轿车以90公里/小时的速度从A地开往B地;公共汽车以60公里/小时的速度从B开往A地,两车同时出发相对而行,两车在C地相遇,相遇后继续前行到达各自的目的地.
(1)多少小时后两车相遇?
(2)小轿车和公共汽车分别到达目的地,计算小轿车的碳足迹为多少?公共汽车的碳中和树木棵数为多少?
(3)根据观察或计算说明,为了减少环境污染,我们应该选择哪种交通工具出行更有利于环保呢?
【正确答案】(1)两车2小时相遇.
(2) 0.015(棵)
(3) 通过观察得出,我们应尽量选择公共交通出行,有利于环保.
【详解】试题分析:(1)x小时两车相遇,根据两车x小时行驶的路程之和为300列出方程求解即可;
(2)小轿车行驶的总路程300公里除以100再乘以行驶100公里的碳足迹(Kg)22.5即可计算出小轿车的碳足迹,公共汽车行驶的总路程300公里除以100再乘以100公里碳中和树木棵数0.005计算即可;
(3)根据表格中提供的数据可知小轿车行驶100公里的碳足迹(Kg)大于公共汽车行驶100公里的碳足迹(Kg),小轿车100公里碳中和树木棵数大于公共汽车100公里碳中和树木棵数,由此可知我们应尽量选择公共交通出行,有利于环保.
解:(1)设x小时两车相遇,
根据题意列方程得90x+60x=300,
解得:x=2,
答:两车2小时相遇;
(2)小轿车到达目的地,碳足迹为22.5×3=67.5(Kg);
公共汽车到达目的地碳中和树木棵数为:0.005×3=0.015(棵);
(3) 通过观察得出,我们应尽量选择公共交通出行,有利于环保.
点睛:本题主要考查了一元方程的实际应用,根据题意列出方程是解决此题的关键.
25. 我们已经学习了“乘方”运算,下面介绍一种新运算,即“对数”运算.
定义:如果(a>0,a≠1,N>0),那么b叫做以a为底N的对数,记作.
例如:因为,所以;因为,所以.
根据“对数”运算的定义,回答下列问题:
(1)填空: , .
(2)如果,求m的值.
(3)对于“对数”运算,小明同学认为有“(a>0,a≠1,M>0,N>0)”,他的说确吗?如果正确,请给出证明过程;如果没有正确,请说明理由,并加以改正.
【正确答案】(1)1,4;(2)m=10 ;(3)没有正确,改正见解析.
【详解】试题分析:(1)根据新定义由61=6、34=81可得log66=1,log381=4;
(2)根据定义知m﹣2=23,解之可得;
(3)设ax=M,ay=N,则logaM=x、logaN=y,根据ax•ay=ax+y知ax+y=M•N,继而得logaMN=x+y,据此即可得证.
试题解析:解:(1)∵61=6,34=81,∴log66=1,log381=4.故答案为1,4;
(2)∵log2(m﹣2)=3,∴m﹣2=23,解得:m=10;
(3)没有正确,设ax=M,ay=N,则logaM=x,logaN=y(a>0,a≠1,M、N均为正数).∵ax•ay=,∴=M•N,∴logaMN=x+y,即logaMN=logaM+logaN.
点睛:本题考查了有理数和整式的混合运算,解题的关键是明确题意,可以利用新定义进行解答问题.
北京市海淀区2022-2023学年七年级上册数学期末专项提升试题(卷二)
一、选一选(本题有10小题,每题3分,共30分)
1. -0.2的相反数是( )
A. -2 B. 2 C. 0.2 D. -5
2. 下列四个数中,的一个数是( )
A. 2 B. C. 0 D. ﹣2
3. 我国倡导的“”建设将促进我国与世界一些国家的互利合作,根据“”地区覆盖总 人口为4400000000人,这个数用科学记数法表示为
A. 4.4×108 B. 4.40×108 C. 4.4×109 D. 4.4×1010
4. 点A,B在数轴上的位置如图所示,其对应的数分别是a和b.对于以下结论:
甲:b−a<0;乙:a+b>0;丙:|a|<|b|;丁:>0;其中正确的是( )
A. 甲乙 B. 丙丁 C. 甲丙 D. 乙丁
5. 是负无理数,下列判断正确的是( )
A. B. C. D.
6. 下列各式计算正确的是( )
A. 5x+x=5x2 B. 3ab2﹣8b2a=﹣5ab2
C. 5m2n﹣3mn2=2mn D. ﹣2a+7b=5ab
7. 将一张长方形纸片折叠成如图所示的形状,则∠ABC等于( )
A. 73° B. 56° C. 68° D. 146°
8. 在直线AB上任取一点O,过点O作射线OC,OD,使OC⊥OD,当∠AOC=30°时,∠BOD的度数是( )
A. 60° B. 120° C. 60°或90° D. 60°或120°
9. 我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满七进一,用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是( )
A. 84 B. 336 C. 510 D. 1326
10. 如图,在数轴上,A1,P两点表示的数分别是-1,-2,作A1关于原点O对称的点得A2,作A2关于点P对称的点得A3,取线段A1A3的中点M1,作M1关于原点O对称的点得A4,作A4关于点P对称的点得A5,取线段A1A5的中点M2,……依此规律,则A8表示的数是( )
A. 4.25 B. 45 C. 4. 75 D. 5
二、填 空 题(本题有6小题,每题4分,共24分)
11. __________.
12. 16的平方根是 .
13. 已知关于x的方程2x+a﹣5=0的解是x=2,则a的值为_______.
14. 如果代数式值为5,那么代数式的值为____________.
15. 如图是用相同长度的小棒摆成的一组有规律的图案,图案①需要4根小棒,图案②需要10根小棒……,按此规律摆下去,第个图案需要小棒________________根(用含有的代数式表示).
16. 书店举行购书优惠:①性购书没有超过100元,没有享受打折优惠;②性购书超过100元但没有超过200元一律打九折;③性购书200元一律打七折.小丽在这次中,两次购书总共付款229.4元,第二次购书原价是次购书原价3倍,那么小丽这两次购书原价的总和是__________元.
三、解 答 题(本题有8小题,共66分)
17. 计算:(1)﹣13+10﹣7 (2)
18. 化简:(1) (2)
19. 先化简,再求值:,其中
20. 解方程: (1) (2)
21. 如图(1),在5×5正方形ABCD中,每个小正方形的边长都是1.
(1)如图(2),连结各条边上的四个点E,F,G,H可得到一个新的正方形,那么这个新正方形的边长是 ;
(2)将新正方形做如下变换,点E向D点运动,同时点F以相同的速度向点A运动,其他两点也做相同变化;当E,F,G,H各点分别运动到AD,AB,BC,CD的什么位置时,所得的新正方形面积是13,在图(3)中画出新正方形,此时AE= ;
(3)在图(1)中作出一条以A为端点的线段AP,使得线段AP=,且点P必须落在横纵线的交叉点上.
22. 如图1是一副三角尺拼成的图案
(1)则∠EBC的度数为 _________ 度;
(2)将图1中的三角尺ABC绕点B旋转到AB⊥BD时,作∠DBC的角平分线BF,直接写出∠EBF的度数是 _________ 度;
(3)将图1中的三角尺ABC绕点B旋转α度(0°<α<90°)能否使∠ABE=2∠DBC?若能,则求出∠EBC的度数;若没有能,说明理由.(图2、图3供参考)
23. 图是一根可伸缩鱼竿,鱼竿是用10节大小没有同的空心套管连接而成.闲置时鱼竿可收缩,完全收缩后,鱼竿长度即为第1节套管的长度(如图1所示);使用时,可将鱼竿的每一节套管都完全拉伸(如图2所示).图3是这根鱼竿所有套管都处于完全拉伸状态下的平面示意图,已知第1节套管长50 cm,第2节套管长46 cm,以此类推,每一节套管均比前一节套管少4 cm,完全拉伸时,为了使相邻两节套管连接并固定,每相邻两节套管间均有相同长度的重叠,设其长度为x cm.
(1)请直接写出第5节套管的长度;
(2)当这根鱼竿完全拉伸时,其长度为311 cm,求x值.
24. 已知数轴上两点A、B对应的数分别为—1,3,点P为数轴上一动点,其对应的数为x.
⑴若点P到点A、点B的距离相等,求点P对应的数;
⑵数轴上是否存在点P,使点P到点A、点B的距离之和为5?若存在,请求出x的值.若没有存在,请说明理由?
⑶当点P以每分钟一个单位长度的速度从O点向左运动时,点A以每分钟5个单位长度向左运动,点B以每分钟20个单位长度向左运动,问它们同时出发,几分钟后点P到点A、点B的距离相等?
北京市海淀区2022-2023学年七年级上册数学期末专项提升试题(卷二)
一、选一选(本题有10小题,每题3分,共30分)
1. -0.2的相反数是( )
A. -2 B. 2 C. 0.2 D. -5
【正确答案】C
【详解】试题解析:的相反数是
故选C.
点睛:只有符号没有同的两个数互为相反数.
2. 下列四个数中,的一个数是( )
A. 2 B. C. 0 D. ﹣2
【正确答案】A
【详解】根据实数比较大小的方法,可得:﹣2<0<<2,故四个数中,的一个数是2.
故选A.
本题考查实数的大小比较,无理数与有理数比较大小可平方后再比较大小.
3. 我国倡导的“”建设将促进我国与世界一些国家的互利合作,根据“”地区覆盖总 人口为4400000000人,这个数用科学记数法表示为
A. 4.4×108 B. 4.40×108 C. 4.4×109 D. 4.4×1010
【正确答案】C
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的值与小数点移动的位数相同.当原数值>1时,n是正数;当原数的值<1时,n是负数.
【详解】解:4 400 000 000=4.4×109,
故选C.
4. 点A,B在数轴上的位置如图所示,其对应的数分别是a和b.对于以下结论:
甲:b−a<0;乙:a+b>0;丙:|a|<|b|;丁:>0;其中正确是( )
A. 甲乙 B. 丙丁 C. 甲丙 D. 乙丁
【正确答案】C
【分析】根据有理数的加法法则判断两数的和、差及积的符号,用两个负数比较大小的方法判断.
【详解】甲:由数轴有,0
甲的说确,
乙:∵0
乙的说法错误,
丙:∵0
丙的说确,
丁:∵0
丁的说法错误;
故选C.
此题考查值,数轴,解题关键在于数轴进行解答.
5. 是负无理数,下列判断正确的是( )
A. B. C. D.
【正确答案】D
【详解】试题解析:是负无理数,
故选D.
6. 下列各式计算正确的是( )
A 5x+x=5x2 B. 3ab2﹣8b2a=﹣5ab2
C. 5m2n﹣3mn2=2mn D. ﹣2a+7b=5ab
【正确答案】B
【详解】试题解析:A.故错误.
B.正确.
C.没有是同类项,没有能合并.故错误.
D. 没有是同类项,没有能合并.故错误.
故选B.
点睛:所含字母相同并且相同字母的指数也相同的项叫做同类项.
7. 将一张长方形纸片折叠成如图所示的形状,则∠ABC等于( )
A. 73° B. 56° C. 68° D. 146°
【正确答案】A
【分析】根据补角的知识可求出∠CBE,从而根据折叠的性质∠ABC=∠ABE=∠CBE,可得出∠ABC的度数.
【详解】如图,
∵∠CBD=34°,
∴∠CBE=180°﹣∠CBD=146°,
由折叠的性质可得
∠ABC=∠ABE=∠CBE=73°.
故选:A
考点:平行线的性质.
8. 在直线AB上任取一点O,过点O作射线OC,OD,使OC⊥OD,当∠AOC=30°时,∠BOD的度数是( )
A. 60° B. 120° C. 60°或90° D. 60°或120°
【正确答案】D
【详解】①当OC、OD在AB的一旁时,
∵OC⊥OD,
∴∠DOC=90°,
∵∠AOC=30°,
∴∠BOD=180°−∠COD−∠AOC=60°
②当OC、OD在AB两旁时,
∵OC⊥OD,∠AOC=30°,
∴∠AOD=60°,
∴∠BOD=180°−∠AOD=120°.
故选D.
9. 我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满七进一,用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是( )
A. 84 B. 336 C. 510 D. 1326
【正确答案】C
【详解】由题意满七进一,可得该图示为七进制数,化为十进制数为:1×73+3×72+2×7+6=510,
故选:C.
点睛:本题考查记数的方法,注意运用七进制转化为十进制,考查运算能力,属于基础题.
10. 如图,在数轴上,A1,P两点表示的数分别是-1,-2,作A1关于原点O对称的点得A2,作A2关于点P对称的点得A3,取线段A1A3的中点M1,作M1关于原点O对称的点得A4,作A4关于点P对称的点得A5,取线段A1A5的中点M2,……依此规律,则A8表示的数是( )
A. 4.25 B. 4.5 C. 4. 75 D. 5
【正确答案】B
【详解】试题解析:∵点表示-1,点表示-2,关于点对称,
∴表示1,
同理可知:表示-5,表示3,表示-7,表示4,表示-6,表示4.5.
故选B.
二、填 空 题(本题有6小题,每题4分,共24分)
11. __________.
【正确答案】1
【详解】试题解析:
故答案为1.
12. 16的平方根是 .
【正确答案】±4
【详解】由(±4)2=16,可得16的平方根是±4,
故±4.
13. 已知关于x的方程2x+a﹣5=0的解是x=2,则a的值为_______.
【正确答案】1
【详解】解:把x=2代入方程,得:4+a﹣5=0,
解得:a=1.
故答案是:1.
14. 如果代数式的值为5,那么代数式的值为____________.
【正确答案】-7
【详解】试题解析:由题意可得:
故答案为
15. 如图是用相同长度的小棒摆成的一组有规律的图案,图案①需要4根小棒,图案②需要10根小棒……,按此规律摆下去,第个图案需要小棒________________根(用含有的代数式表示).
【正确答案】6n-2
【详解】观察图案可知,每下一幅图案比前一幅图案多6根小棒,找出6与n的联系即可.
解:如图可知,后一幅图总是比前一幅图多两个菱形,且多6根小棒,
图案(1)需要小棒:6×1-2=4(根),
图案(2)需要小棒:6×2-2=10(根),
则第n个图案需要小棒:(6n-2)根.
故答案为6n-2.
16. 书店举行购书优惠:①性购书没有超过100元,没有享受打折优惠;②性购书超过100元但没有超过200元一律打九折;③性购书200元一律打七折.小丽在这次中,两次购书总共付款229.4元,第二次购书原价是次购书原价的3倍,那么小丽这两次购书原价的总和是__________元.
【正确答案】248或296
【详解】试题分析:设次购书的原价为x元,则第二次购书的原价为3x元.根据x的取值范围分段考虑,根据“付款金额=次付款金额+第二次付款金额”即可列出关于x的一元方程,解方程即可得出结论.
设次购书的原价为x元,则第二次购书的原价为3x元,
依题意得:①当0<x≤时,x+3x=229.4, 解得:x=57.35(舍去);
②当<x≤时,x+×3x=229.4, 解得:x=62,
此时两次购书原价总和为:4x=4×62=248;
③当<x≤100时,x+×3x=229.4, 解得:x=74,
此时两次购书原价总和为:4x=4×74=296.
综上可知:小丽这两次购书原价的总和是248或296元
考点:一元方程的应用
三、解 答 题(本题有8小题,共66分)
17. 计算:(1)﹣13+10﹣7 (2)
【正确答案】⑴ -10 ⑵ -3
【详解】试题分析:按照运算顺序进行运算即可.
试题解析:原式
原式
18. 化简:(1) (2)
【正确答案】⑴ ; ⑵ .
【详解】试题分析:合并同类项即可.
先去括号,再合并同类项即可.
试题解析:原式
原式
19. 先化简,再求值:,其中
【正确答案】,-7
【详解】试题分析:原式去括号合并得到最简结果,利用非负数的性质求出与的值,代入原式计算即可得到结果.
试题解析:
原式
当时,
原式
20. 解方程: (1) (2)
【正确答案】⑴ ⑵
【详解】试题分析:按照解一元方程的步骤解方程即可.
试题解析:
点睛:解一元方程的步骤:去分母,去括号,移项,合并同类项,把系数化为1.
21. 如图(1),在5×5正方形ABCD中,每个小正方形的边长都是1.
(1)如图(2),连结各条边上的四个点E,F,G,H可得到一个新的正方形,那么这个新正方形的边长是 ;
(2)将新正方形做如下变换,点E向D点运动,同时点F以相同的速度向点A运动,其他两点也做相同变化;当E,F,G,H各点分别运动到AD,AB,BC,CD的什么位置时,所得的新正方形面积是13,在图(3)中画出新正方形,此时AE= ;
(3)在图(1)中作出一条以A为端点的线段AP,使得线段AP=,且点P必须落在横纵线的交叉点上.
【正确答案】(1) ;(2) 2或3;(3)见解析.
【详解】试题分析:根据勾股定理进行运算即可.
根据正方形的面积求出边长,即可求出.
根据勾股定理即可画出点的位置.
试题解析:
⑴边长为:
故答案为
如图所示或3,
⑶ 如图所示,即为所求.
22. 如图1是一副三角尺拼成的图案
(1)则∠EBC的度数为 _________ 度;
(2)将图1中的三角尺ABC绕点B旋转到AB⊥BD时,作∠DBC的角平分线BF,直接写出∠EBF的度数是 _________ 度;
(3)将图1中的三角尺ABC绕点B旋转α度(0°<α<90°)能否使∠ABE=2∠DBC?若能,则求出∠EBC的度数;若没有能,说明理由.(图2、图3供参考)
【正确答案】⑴ 150° ⑵ 75°或165° ⑶ 120°或80°
【详解】试题分析:(1)是由一个直角和一个60°的角组成的;
分两种情况画出图,直接写出的度数.
分没有同方向旋转,求得,等量关系为 用表示出这个等量关系.进而求解.
试题解析:
的度数是或.
故答案为或.
(3)种情况:
若逆时针旋转α度 如图2:
据题意得
得
第二种情况,若逆时针旋转α度
据题意得
得
第三种情况:若顺时针旋转α度,如图3,
据题意得
得
没有合题意,舍去.
故或
23. 图是一根可伸缩的鱼竿,鱼竿是用10节大小没有同的空心套管连接而成.闲置时鱼竿可收缩,完全收缩后,鱼竿长度即为第1节套管的长度(如图1所示);使用时,可将鱼竿的每一节套管都完全拉伸(如图2所示).图3是这根鱼竿所有套管都处于完全拉伸状态下的平面示意图,已知第1节套管长50 cm,第2节套管长46 cm,以此类推,每一节套管均比前一节套管少4 cm,完全拉伸时,为了使相邻两节套管连接并固定,每相邻两节套管间均有相同长度的重叠,设其长度为x cm.
(1)请直接写出第5节套管的长度;
(2)当这根鱼竿完全拉伸时,其长度为311 cm,求x的值.
【正确答案】(1)34cm;(2)每相邻两节套管间重叠的长度为1 cm.
【分析】(1)根据“第n节套管的长度=第1节套管的长度﹣4×(n﹣1)”,代入数据即可得出结论;
(2)同(1)方法求出第10节套管重叠的长度,设每相邻两节套管间的长度为xcm,根据“鱼竿长度=每节套管长度相加﹣(10﹣1)×相邻两节套管间的长度”,得出关于x的一元方程,解方程即可得出结论.
【详解】解:(1)第5节套管的长度为:50﹣4×(5﹣1)=34(cm).
(2)第10节套管长度为:50﹣4×(10﹣1)=14(cm),
设每相邻两节套管间重叠的长度为xcm,
根据题意得:(50+46+42+…+14)﹣9x=311,
即:320﹣9x=311,
解得:x=1.
答:每相邻两节套管间重叠的长度为1cm.
24. 已知数轴上两点A、B对应的数分别为—1,3,点P为数轴上一动点,其对应的数为x.
⑴若点P到点A、点B的距离相等,求点P对应的数;
⑵数轴上是否存在点P,使点P到点A、点B的距离之和为5?若存在,请求出x的值.若没有存在,请说明理由?
⑶当点P以每分钟一个单位长度的速度从O点向左运动时,点A以每分钟5个单位长度向左运动,点B以每分钟20个单位长度向左运动,问它们同时出发,几分钟后点P到点A、点B的距离相等?
【正确答案】⑴ x=1⑵ x=—1.5或x=3.5
⑶ 时,P到A、B的距离相等
【分析】(1)计算A、B两点间的距离,再取中点并写出点表示的数;
(2)分情况讨论:当P在-1左边时,当P在2的右边时,再求P的坐标;
(3)画图分析,设t分后有PA=PB,再求出 t的值即可;
【详解】(1)如图所示,AB中点表示的数是 ,即点P对应的数是1;
(2)解:设存在点,使到、距离和为.
①当时,有:,
②当时,有:,
存在和能使条件成立
(3)解:设t分后到、距离相等
①
当在左,在右时,
..
有
②
当在左,在右
没有可能出现.舍弃;
③当与重合时,也符合情况,
即:=,
解得:
综上所述,或分钟到、距离相等.
2022-2023学年北京市海淀区七年级上册数学期中专项提升模拟(卷一卷二)含解析: 这是一份2022-2023学年北京市海淀区七年级上册数学期中专项提升模拟(卷一卷二)含解析,共32页。试卷主要包含了选一选,填 空 题,解 答 题等内容,欢迎下载使用。
2022-2023学年北京市海淀区七年级上册数学期中专项突破模拟(卷一卷二)含解析: 这是一份2022-2023学年北京市海淀区七年级上册数学期中专项突破模拟(卷一卷二)含解析,共41页。试卷主要包含了选一选,填 空 题,解 答 题等内容,欢迎下载使用。
北京市海淀区2022-2023学年七年级上册数学期末专项提升试题(AB卷)含解析: 这是一份北京市海淀区2022-2023学年七年级上册数学期末专项提升试题(AB卷)含解析,共34页。试卷主要包含了填 空 题,选一选,解 答 题等内容,欢迎下载使用。












