

2022-2023学年江苏省南京市九年级上册数学期末专项提升模拟卷(卷一卷二)含解析
展开2022-2023学年江苏省南京市九年级上册数学期末专项提升模拟卷(卷一)
一、选一选 (每小题3分,共60分)
1. 下列根式中,属于最简二次根式的是
A. B. C. D.
2. 下列计算正确的是( )
A B. C. D.
3. 已知,则的值为( )
A. B. C. D.
4. 若是一元二次方程,则m的值为
A. ±2 B. 2 C. -2 D. 以上都没有对
5. 用配方法解方程, ,变形正确的是( )
A. B.
C. D.
6. 设x1、x2是方程2x2﹣4x﹣3=0两根,则x1+x2的值是( )
A. 2 B. ﹣2 C. D. ﹣
7. 关于x的方程 =0有两个没有相等的实数根,则k的取值范围是( )
A. k≥0 B. k>0 C. k≥﹣1 D. k>﹣1
8. 若,且3a-2b+c=3,则2a+4b-3c的值是( ).
A. 14 B. 42 C. 7 D.
9. 如图,在△ABC中,M,N分别是边AB,AC中点,则△AMN的面积与四边形MBCN的面积比为
A. B. C. D.
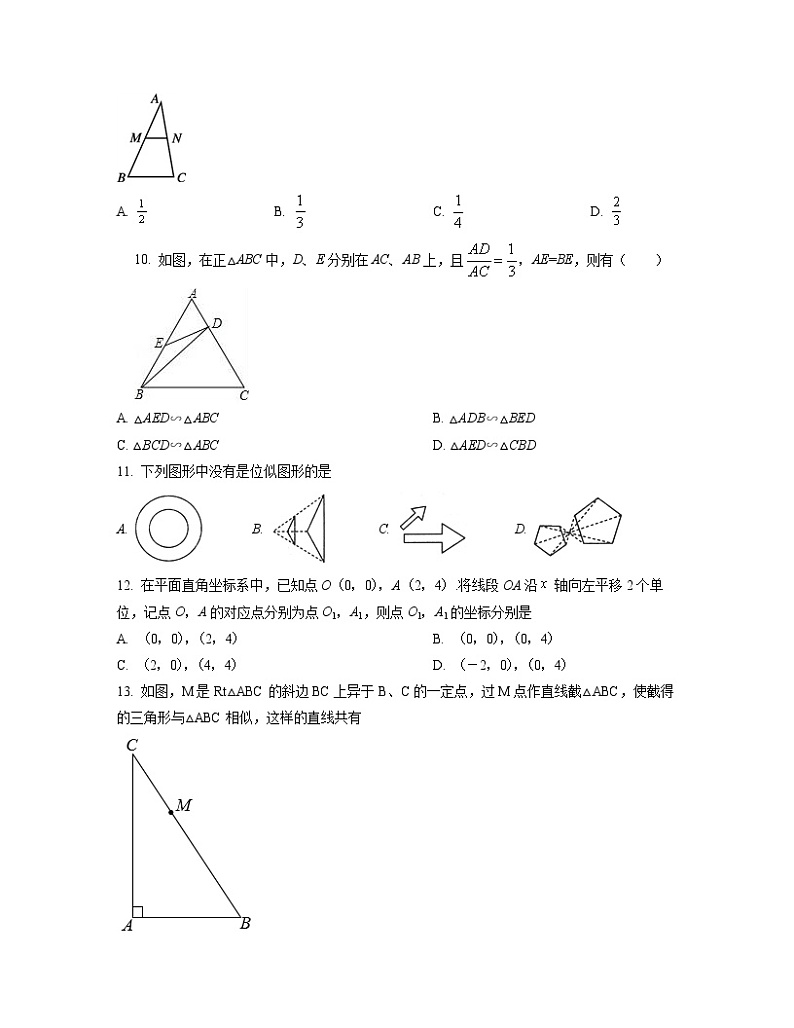
10. 如图,在正△ABC中,D、E分别在AC、AB上,且,AE=BE,则有( )
A. △AED∽△ABC B. △ADB∽△BED
C. △BCD∽△ABC D. △AED∽△CBD
11. 下列图形中没有是位似图形的是
A. B. C. D.
12. 在平面直角坐标系中,已知点O(0,0),A(2,4).将线段OA沿 轴向左平移2个单位,记点O,A的对应点分别为点O1,A1,则点O1,A1的坐标分别是
A. (0,0),(2,4) B. (0,0),(0,4)
C. (2,0),(4,4) D. (-2,0),(0,4)
13. 如图,M是Rt△ABC的斜边BC上异于B、C的一定点,过M点作直线截△ABC,使截得的三角形与△ABC相似,这样的直线共有
A. 1条 B. 2条 C. 3条 D. 4条
14. 在△ABC中,∠C=90°,tanA=,那么sinA值是( )
A. B. C. D.
15. 如图,在△ABC中,∠ABC=90°,DE垂直平分AC,垂足为O,AD∥BC,且AB=3,BC=4,则AD的长为( ).
A. B. C. D.
16. 化简:的结果是
A. B.
C. D.
17. 某人在坡角为的山坡上种树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为( )
A. 5cos B. C. 5sin D.
18. 如图,在菱形ABCD中,DE⊥AB于E,cosA=,BE=2,则tan∠DBE的值是( )
A. 2 B. C. D.
19. 下列说确的是( )
A. “明天降雨的概率是60%”表示明天有60%的时间都在降雨
B. “抛一枚硬币正面朝上的概率为50%”表示每抛2次就有正面朝上
C. “中奖的概率为1%”表示买100张肯定会中奖
D. “抛一枚正方体骰子,朝上的点数为2的概率为”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一发生的概率稳定在附近
20. 二次函数y=-x2+6-7,当取值为t≤x≤t+2时,有值y值=-(t-3)2+2,则的取值范围为
A. t≤0 B. 0≤t≤3 C. t≥3 D. 以上都没有对
二、填 空 题(每小题3分,共15分)
21. 在二次根式中的取值范围是__________.
22. 如果2+是方程的一个根,那么的值是__________.
23. 如图,电灯P在横杆AB的上方,AB在灯光下的影子为CD,ABCD,AB=2m,CD=6m,点P到CD的距离是3m,则P到 AB的距离是_____m.
24. 已知,则=__________.
25. 如图为抛物线的部分图象,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),下列结论:
①4ac<b2
②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3
③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3
⑤当x<0时,y随x增大而增大
其中正确的结论是____.
三、解 答 题(本题共9个小题,共75分)
26. 计算:4cos30°﹣|﹣2|+()0﹣+(﹣)﹣2.
27. 解方程:.
28. 已知关于x的方程.
(1)求证方程有两个没有相等的实数根.
(2)当m为何值时,方程的两根互为相反数?并求出此时方程的解.
29. 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:∠DFA=∠ECD;
(2)△ADF与△DEC相似吗?为什么?
(3)若AB=4,AD=3,AE=3,求AF的长.
30. 已知:如图,在山脚的C处测得山顶A的仰角为45°,沿着坡度为30°的斜坡前进400米到D处(即∠ 米),测得A的仰角为,求山的高度AB.
31. 一个没有透明的口袋中装有4个完全相同的小球,分别标有数字1,2,3,4,另外有一个可以旋转的圆盘,被分成面积相等的3个扇形区域,分别标有数字1,2,3(如图所示).
(1)从口袋中摸出一个小球,所摸球上的数字大于2的概率为 ;
(2)小龙和小东想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于5,那么小龙去;否则小东去.你认为游戏公平吗?请用树状图或列表法说明理由.
32. 在北京2008年第29届奥运会前夕,某超市在中发现:奥运会吉祥物— “福娃”平均每天可售出20套,每件盈利40元.为了迎接奥运会,商场决定采取适当的降价措施,扩大量,增加盈利,尽快减少库存.经市场发现:如果每套降价4元,那么平均每天就可多售出8套.要想平均每天在吉祥物上盈利1200元,那么每套应降价多少?
33. 如图,在△ABC中,AB=6cm,BC=12cm,∠B=90°.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发,设移动时间为t(s).
(1)当t=4时,求△PBQ的面积;
(2)当t为多少时,四边形APQC的面积最小?最小面积是多少?
(3)当t为多少时,△PQB与△ABC相似.
34. 如图,二次函数的图象坐标原点,与轴的另一个交点为A(-2,0).
(1)求二次函数解析式
(2)在抛物线上是否存在一点P,使△AOP的面积为3,若存在请求出点P的坐标,若没有存在,请说明理由.
2022-2023学年江苏省南京市九年级上册数学期末专项提升模拟卷(卷一)
一、选一选 (每小题3分,共60分)
1. 下列根式中,属于最简二次根式的是
A. B. C. D.
【正确答案】B
【详解】试题解析:A、被开方数含能开得尽方的因数或因式,故A错误;
B、被开方数没有含分母;被开方数没有含能开得尽方的因数或因式,故B正确;
C、被开方数含分母,故C错误;
D、被开方数含能开得尽方的因数或因式,故D错误.
故选B.
本题考查最简二次根式的定义.根据最简二次根式的定义,最简二次根式必须满足两个条件:被开方数没有含分母;被开方数没有含能开得尽方的因数或因式.
2. 下列计算正确的是( )
A. B. C. D.
【正确答案】C
【详解】试题分析:根据合并同类二次根式,可知没有能计算,故没有正确;
根据二次根式的除法,可知=,故没有正确;
根据二次根式的性质,可知,故正确;
根据最简二次根式的概念,可知,故没有正确.
故选C.
3. 已知,则的值为( )
A. B. C. D.
【正确答案】A
【详解】解:由,得
,
解得.
2xy=2×2.5×(-3)=-15,
故选:A.
4. 若是一元二次方程,则m的值为
A. ±2 B. 2 C. -2 D. 以上都没有对
【正确答案】C
【详解】试题解析:根据题意得:,
解得:m=-2.
故选C.
本题利用了一元二次方程的概念.只有一个未知数且未知数次数为2的整式方程叫做一元二次方程,一般形式是ax2+bx+c=0(且a≠0).特别要注意a≠0的条件.这是在做题过程中容易忽视的知识点.
5. 用配方法解方程, ,变形正确的是( )
A. B.
C. D.
【正确答案】A
【分析】根据配方法的解题步骤变形即可;
【详解】,
,
,
;
故答案选A.
本题主要考查了一元二次方程配方法的应用,准确变形判断是解题的关键.
6. 设x1、x2是方程2x2﹣4x﹣3=0的两根,则x1+x2的值是( )
A. 2 B. ﹣2 C. D. ﹣
【正确答案】A
【详解】试题解析:∵,是方程的两根,
根据一元二次方程根与系数的关系得:+=2
故选A.
7. 关于x的方程 =0有两个没有相等的实数根,则k的取值范围是( )
A. k≥0 B. k>0 C. k≥﹣1 D. k>﹣1
【正确答案】A
【分析】
【详解】解:∵方程x2+2x−1=0有两个没有相等的实数根,
∴k≥0,且△>0,即(2)2-4×1×(-1)>0,
解得k>-1.
∴k的取值范围是k≥0.
故选:A.
一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个没有相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.
8. 若,且3a-2b+c=3,则2a+4b-3c的值是( ).
A. 14 B. 42 C. 7 D.
【正确答案】D
【分析】
【详解】解:设a=5k,则b=7k,c=8k,
又3a-2b+c=3,则15k-14k+8k=3,
得k=,
即a=,b=,c=,
所以2a+4b-3c=.
故选D.
9. 如图,在△ABC中,M,N分别是边AB,AC的中点,则△AMN的面积与四边形MBCN的面积比为
A. B. C. D.
【正确答案】B
【详解】解:∵M,N分别是边AB,AC的中点,
∴MN是△ABC的中位线,
∴MN∥BC,且MN=BC,
∴△AMN∽△ABC,
∴,
∴△AMN的面积与四边形MBCN的面积比为1:3.
故选B.
本题考查了相似三角形的判定与性质,解答本题的关键是得出MN是△ABC的中位线,判断△AMN∽△ABC,要掌握相似三角形的面积比等于相似比平方.
10. 如图,在正△ABC中,D、E分别在AC、AB上,且,AE=BE,则有( )
A. △AED∽△ABC B. △ADB∽△BED
C. △BCD∽△ABC D. △AED∽△CBD
【正确答案】D
【详解】解:因为△ABC是正三角形,
所以∠A=∠C=60°,
可设AD=a,则AC=3a,
而AB=AC=BC=3a,
所以AE=BE=a,
所以==,
又==,
所以=,∠A=∠C=60°,
故△AED∽△CBD,
故选D.
11. 下列图形中没有是位似图形的是
A. B. C. D.
【正确答案】C
【分析】对应顶点连线相交于一点的两个相似多边形叫位似图形.
【详解】根据位似图形的概念,A、B、D三个图形中的两个图形都是位似图形;
C中的两个图形没有符合位似图形的概念,对应顶点没有能相交于一点,故没有是位似图形.
故选C.
此题主要考查了位似图形,注意位似与相似既有联系又有区别,相似仅要求两个图形形状完全相同;而位似是在相似的基础上要求对应点的连线相交于一点.
12. 在平面直角坐标系中,已知点O(0,0),A(2,4).将线段OA沿 轴向左平移2个单位,记点O,A的对应点分别为点O1,A1,则点O1,A1的坐标分别是
A. (0,0),(2,4) B. (0,0),(0,4)
C. (2,0),(4,4) D. (-2,0),(0,4)
【正确答案】D
【详解】试题解析:线段OA沿x轴向左平移2个单位,只须让原来的横坐标都减2,纵坐标没有变即可.
∴新横坐标分别为0-2=-2,2-2=0,即新坐标为(-2,0),(0,4).
本题考查图形的平移变换,关键是要懂得左右平移点的纵坐标没有变,而上下平移时点的横坐标没有变.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
13. 如图,M是Rt△ABC的斜边BC上异于B、C的一定点,过M点作直线截△ABC,使截得的三角形与△ABC相似,这样的直线共有
A. 1条 B. 2条 C. 3条 D. 4条
【正确答案】C
【分析】过点M作直线与另一边相交,使所得的三角形与原三角形有一个公共角,只要再作一个直角就可以.
【详解】过点M作直线与另一边相交,使所得的三角形与原三角形有一个公共角,只要再作一个直角就可以.因此,
∵截得的三角形与△ABC相似,
∴过点M作AB的垂线,或作AC的垂线,或作BC的垂线,所得三角形满足题意
∴过点M作直线l共有三条.
故选C.
14. 在△ABC中,∠C=90°,tanA=,那么sinA的值是( )
A. B. C. D.
【正确答案】B
【详解】∵tanA=,
∴设BC=x,AC=3x,
由勾股定理,得AB=x,
∴sinA=,
故选:B.
15. 如图,在△ABC中,∠ABC=90°,DE垂直平分AC,垂足为O,AD∥BC,且AB=3,BC=4,则AD的长为( ).
A. B. C. D.
【正确答案】B
【详解】试题解析:∵Rt△ABC中,∠ABC=90°,AB=3,BC=4,
∴AC=,
∵DE垂直平分AC,垂足为O,
∴OA=AC=,∠AOD=∠B=90°,
∵AD∥BC,
∴∠A=∠C,
∴△AOD∽△CBA,
∴,即,解得AD=.
故选B.
16. 化简:的结果是
A. B.
C. D.
【正确答案】C
【详解】YAJGQESR:∵1-sin52°>0,1-tan52°<0,
∴=1-sin52°-tan52°+1=2-sin52°-tan52°.
故选C.
本题考查的是二次根式的化简,掌握二次根式的性质和正弦、正切的增减性是解题的关键.
17. 某人在坡角为山坡上种树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为( )
A. 5cos B. C. 5sin D.
【正确答案】B
【分析】利用所给的角的余弦值求解即可.
【详解】由题意可知:BC=5米,∠CBA=∠α,
∴AB==.
故选B.
本题主要考查学生对坡度、坡角的理解及运用,熟练掌握解直角三角形的应用是解题的关键.
18. 如图,在菱形ABCD中,DE⊥AB于E,cosA=,BE=2,则tan∠DBE的值是( )
A. 2 B. C. D.
【正确答案】A
【分析】在直角三角形ADE中,cosA== ,可以求得AB,再利用勾股定理求得DE,即可求得 .
【详解】解:设菱形的边长为t
故选A
本题考查了菱形的性质和解直角三角形中三角函数的应用,要熟练掌握好边角之间的关系.
19. 下列说确的是( )
A. “明天降雨的概率是60%”表示明天有60%的时间都在降雨
B. “抛一枚硬币正面朝上的概率为50%”表示每抛2次就有正面朝上
C. “中奖的概率为1%”表示买100张肯定会中奖
D. “抛一枚正方体骰子,朝上的点数为2的概率为”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一发生的概率稳定在附近
【正确答案】D
【分析】根据概率是指某件事发生的可能性为多少,随着试验次数的增加,稳定在某一个固定数附近,可得答案.
【详解】解:A. “明天降雨的概率是60%”表示明天下雨的可能性较大,故A没有符合题意;
B. “抛一枚硬币正面朝上的概率为”表示每次抛正面朝上的概率都是,故B没有符合题意;
C. “中奖的概率为1%”表示买100张有可能中奖.故C没有符合题意;
D. “抛一枚正方体骰子,朝上的点数为2的概率为”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一发生的概率稳定在附近,故D符合题意;
故选D
本题考查了概率意义,正确理解概率的含义是解决本题的关键.
20. 二次函数y=-x2+6-7,当取值为t≤x≤t+2时,有值y值=-(t-3)2+2,则的取值范围为
A. t≤0 B. 0≤t≤3 C. t≥3 D. 以上都没有对
【正确答案】C
【详解】试题解析:∵y=-x2+6x-7=-(x-3)2+2,
当t≤3≤t+2时,即1≤t≤3时,函数为增函数,
ymax=f(3)=2,与ymax=-(t-3)2+2矛盾.
当3≥t+2时,即t≤1时,ymax=f(t+2)=-(t-1)2+2,与ymax=-(t-3)2+2矛盾.
当3≤t,即t≥3时,ymax=f(t)=-(t-3)2+2与题设相等,
故t的取值范围t≥3,
故选C.
二、填 空 题(每小题3分,共15分)
21. 在二次根式中的取值范围是__________.
【正确答案】x<1
【详解】试题解析:若二次根式有意义,
则<0,
解得x<1.
故x<1.
本题考查二次根式及分式有意义的条件;用到的知识点为:二次根式有意义,被开方数为非负数;分式有意义,分母没有为0.
22. 如果2+是方程的一个根,那么的值是__________.
【正确答案】4
【详解】试题解析:把2+代入方程中可得(2+)2-c(2+)+1=0,
解得c=4.
直接根据方程的解的定义把c的值代入方程求解即可.主要考查了方程的解的定义和无理数的运算,在运算过程中要注意分母有理化.
23. 如图,电灯P在横杆AB上方,AB在灯光下的影子为CD,ABCD,AB=2m,CD=6m,点P到CD的距离是3m,则P到 AB的距离是_____m.
【正确答案】1
【分析】根据ABCD,易得PABPCD,根据相似三角形对应高之比等于对应边之比,列出方程求解即可.
【详解】解:∵ABCD,
∴∠PAB=∠C,∠PBA=∠D,
∴PABPCD,
∴,
∴,
∴P到AB的距离为1m.
故1.
此题考查了相似三角形的应用和投影问题,解题的关键是把实际问题抽象到相似三角形中,利用相似三角形对应高的比等于相似比,列出方程,通过解方程求出P到AB的距离.
24. 已知,则=__________.
【正确答案】
【详解】试题解析:∵sin2α+cos2α=1,
∴(sinα+cosα)2-2sinα•cosα=1,
∵sinα+cosα=,
∴sinα•cosα=.
25. 如图为抛物线的部分图象,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),下列结论:
①4ac<b2
②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3
③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3
⑤当x<0时,y随x增大而增大
其中正确的结论是____.
【正确答案】①②⑤
【分析】利用抛物线与x轴的交点个数可对①进行判断;利用抛物线的对称性得到抛物线与x轴的一个交点坐标为(3,0),则可对②进行判断;由对称轴方程得到b=-2a,然后根据x=-1时函数值为0可得到3a+c=0,则可对③进行判断;根据抛物线在x轴上方所对应的自变量的范围可对④进行判断,根据抛物线的性质判断⑤即可.
【详解】解:∵抛物线与x轴有2个交点,
∴b2-4ac>0,即4ac<b2,所以①正确;
∵抛物线的对称轴为直线x=1,
而点(-1,0)关于直线x=1的对称点的坐标为(3,0),
∴方程ax2+bx+c=0的两个根是x1=-1,x2=3,所以②正确;
∵x==1,即b=-2a,
而x=-1时,y=0,即a-b+c=0,
∴a+2a+c=0,
∴3a+c=0,所以③错误;
由图象知,当y>0时,x的取值范围是-1<x<3,所以④错误;
∵抛物线的对称轴为直线x=1,
∴当x<1时,y随x增大而增大,
∴当x<0时,y随x增大而增大,所以⑤正确;
即正确的个数是3个,
故①②⑤
本题考查了二次函数图象与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点位置:抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.
三、解 答 题(本题共9个小题,共75分)
26. 计算:4cos30°﹣|﹣2|+()0﹣+(﹣)﹣2.
【正确答案】8.
【分析】代入角的三角函数值,按照实数的混合运算法则计算即可得答案.
【详解】4cos30°﹣|﹣2|+()0﹣+(﹣)-2
=
=
=8.
本题考查角的三角函数值、零指数幂、负整数指数幂及二次根式的性质与化简,熟练掌握实数的混合运算法则,熟记角的三角函数值是解题关键.
27. 解方程:.
【正确答案】=3,=.
【详解】试题分析:方程的左边提取公因式x﹣3,即可分解因式,因而方程利用因式分解法求解.
试题解析:原式可化为:(x﹣3)(x﹣3+4x)=0,
∴x﹣3=0或5x﹣3=0,
解得=3,=.
考点:解一元二次方程——因式分解法.
28. 已知关于x的方程.
(1)求证方程有两个没有相等的实数根.
(2)当m为何值时,方程的两根互为相反数?并求出此时方程的解.
【正确答案】(1)证明见解析;(2),
【分析】(1)先计算出△=(m+2)2﹣4(2m﹣1),变形得到△=(m﹣2)2+4,由于(m﹣2)2≥0,则△>0,然后根据△的意义得到方程有两个没有相等的实数根;
(2)利用根与系数的关系得到x1+x2=0,即m+2=0,解得m=﹣2,则原方程化为x2﹣5=0,然后利用直接开平方法求解.
【详解】(1)证明:△=(m+2)2﹣4(2m﹣1)
=m2﹣4m+8
=(m﹣2)2+4,
∵(m﹣2)2≥0,
∴(m﹣2)2+4>0,
即△>0,
所以方程有两个没有相等的实数根;
(2)设方程的两个根为x1,x2,由题意得:
x1+x2=0,即m+2=0,解得m=﹣2,
当m=﹣2时,方程两根互为相反数,
当m=﹣2时,原方程为x2﹣5=0,
解得:x1=﹣,x2=.
根的判别式;根与系数的关系.
29. 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:∠DFA=∠ECD;
(2)△ADF与△DEC相似吗?为什么?
(3)若AB=4,AD=3,AE=3,求AF的长.
【正确答案】(1)详见解析;(2)△ADF∽△DEC,理由详见解析;(3)AF=2.
【分析】(1)因为∠AFE=∠B,平行四边形的邻角互补可得:∠B+∠ECD=180°;,等角的补角相等,所以∠AFE的领补角∠DFA=∠ECD;
(2)根据两角对应相等的两个三角形相似证明;
(3) 由平行四边形ABCD中,过点A作AE⊥BC,AB=4,AD=3,AE=3,由勾股定理可求得DE的长,又由∠AFE=∠B,易证得△ADF∽△DEC,然后由相似三角形的对应边成比例,即可求得答案.
【详解】(1)证明:∵∠AFE∠DFA=180°,又∵四边形ABCD为平行四边形,∴∠B+∠ECD=180°,又∵∠B=∠AFE,∴∠DFA=∠ECD.
(2)解:△ADF∽△DEC.∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD,∴∠ADF=∠CED,∠B+∠C=180°,∵∠AFE+∠AFD=180°,∠AFE=∠B,∴∠AFD=∠C,∴△ADF∽△DEC.
(3)解:∵四边形ABCD是平行四边形,∴AD∥BC,CD=AB=4,又∵AE⊥BC,∴AE⊥AD,在Rt△ADE中,DE= ==6 ,∵△ADF∽△DEC,∴= ,∴=,AF=2 .
本题考查相似三角形的判定与性质、平行四边形的性质以及勾股定理.此题难度适中,注意掌握数形思想的应用.
30. 已知:如图,在山脚的C处测得山顶A的仰角为45°,沿着坡度为30°的斜坡前进400米到D处(即∠ 米),测得A的仰角为,求山的高度AB.
【正确答案】(200+200)米.
【详解】试题分析:首先根据题意分析图形;作DE⊥AB于E,作DF⊥BC于F,构造两个直角三角形,分别求解可得DF与EA的值,再利用图形关系,进而可求出答案.
试题解析:作DE⊥AB于E,作DF⊥BC于F,在RtΔCDF中,
==200(米)
=(米)
在中,,设DE=米,
∴(米)
在矩形DEBF中,BE=DF=200米,
在,
∴AB=BC,
即:
∴x=200,
∴米.
31. 一个没有透明的口袋中装有4个完全相同的小球,分别标有数字1,2,3,4,另外有一个可以旋转的圆盘,被分成面积相等的3个扇形区域,分别标有数字1,2,3(如图所示).
(1)从口袋中摸出一个小球,所摸球上的数字大于2的概率为 ;
(2)小龙和小东想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于5,那么小龙去;否则小东去.你认为游戏公平吗?请用树状图或列表法说明理由.
【正确答案】(1);(2)游戏公平.
【分析】(1)因为口袋中有4个小球,大于2的有两个分别是3,4,由此可求出其概率.
(2)游戏公平,分别求出题目各自获胜的概率,比较概率是否相等,即可判定游戏是否公平.
【详解】解:(1)∵的口袋中装有4个完全相同的小球,分别标有数字1,2,3,4,
∴从口袋中摸出一个小球,所摸球上的数字大于2的概率为;
故答案为;
(2)游戏公平.
列举所有等可能的结果12个:
1
2
3
4
1
2
3
4
5
2
3
4
5
6
3
4
5
6
7
∴所摸球上的数字与圆盘上转出数字之和小于5的概率为P=,
∴游戏公平.
本题考查游戏公平性和求概率,解题关键是熟练运用概率公式和列表法求出概率.
32. 在北京2008年第29届奥运会前夕,某超市在中发现:奥运会吉祥物— “福娃”平均每天可售出20套,每件盈利40元.为了迎接奥运会,商场决定采取适当的降价措施,扩大量,增加盈利,尽快减少库存.经市场发现:如果每套降价4元,那么平均每天就可多售出8套.要想平均每天在吉祥物上盈利1200元,那么每套应降价多少?
【正确答案】每套应降价20元.
【详解】试题分析:设每套降价x元,那么就多卖出2x套,根据扩大量,增加盈利,尽快减少库存,每天在吉祥物上盈利1200元,可列方程求解.
试题解析:设每套降价x元,
由题意得:(40-x)(20+2x)=1200
即2x2-60x+400=0,
∴x2-30x+200=0,
∴(x-10)(x-20)=0,
解之得:x=10或x=20
为了减少库存,所以x=20.
因此,每套应降价20元.
考点: 一元二次方程的应用.
33. 如图,在△ABC中,AB=6cm,BC=12cm,∠B=90°.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发,设移动时间为t(s).
(1)当t=4时,求△PBQ的面积;
(2)当t为多少时,四边形APQC面积最小?最小面积是多少?
(3)当t为多少时,△PQB与△ABC相似.
【正确答案】|(1)8cm2;(2)27 cm2;(3)1.2或3.
【详解】试题分析:(1)根据直角三角形的面积公式和路程=速度×时间进行求解即可;
(2)四边形APQC的面积=△ABC的面积﹣△PBQ的面积,再根据配方法即可求解;
(3)分两种情况讨论:和,求出对应的t即可.
试题解析:(1)当时,AP=2,BQ=4,PB=4,∴=();
(2)∵AP=,BQ=,PB=,∴ =
=,∴当=3时,有最小值27;
(3)∵△PQB、△ABC是直角三角形,∴由,即,解得,由,即,解得,∴当或时,△PQB与△ABC相似.
考点:1.一元二次方程的应用;2.二次函数的应用;3.几何动点问题.
34. 如图,二次函数的图象坐标原点,与轴的另一个交点为A(-2,0).
(1)求二次函数的解析式
(2)在抛物线上是否存在一点P,使△AOP的面积为3,若存在请求出点P的坐标,若没有存在,请说明理由.
【正确答案】(1)y=-x2-2x;(2)(3,-3),(1,-3).
【分析】(1)把点(0,0)和点A(-2,0)分别代入函数关系式来求b、c的值;
(2)设点P的坐标为(x,-x2-2x),利用三角形的面积公式得到-x2-2x=±3,通过解方程来求x的值,则易求点P的坐标.
【详解】解:(1)∵二次函数y=-x2+bx+c的图象坐标原点(0,0)
∴c=0.
又∵二次函数y=-x2+bx+c的图象过点A(-2,0)
∴-(-2)2-2b+0=0,
∴b=-2.
∴二次函数的解析式:y=-x2-2x;
(2)存在一点P,满足S△AOP=3.
设点P的坐标为(x,-x2-2x)
∵S△AOP=3
∴×2×|-x2-2x|=3
∴-x2-2x=±3.
当-x2-2x=3时,此方程无解;
当-x2-2x=-3时,
解得 x1=-3,x2=1.
∴点P的坐标为(-3,-3)或(1,-3).
本题考查了抛物线与x轴的交点,解(1)题时,实际上利用待定系数法来求抛物线的解析式.
2022-2023学年江苏省南京市九年级上册数学期末专项提升模拟卷(卷二)
一、选一选(每题2分,共12分)
1. 下列函数解析式中,一定为二次函数的是( )
A. y=3x-1 B. y=ax2+bx+c C. s=2t2-2t+1 D. y=x2+
2. 若一组数据2,3,4,5,的方差与另一组数据5,6,7,8,9的方差相等,则的值为( ).
A. 1 B. 6
C. 1或6 D. 5或6
3. 下列表格是二次函数自变量与函数值的对应值,判断方程(,,,为常数)的一个解得范围是( )
A. B.
C. D.
4. 已知函数的图象如图,那么关于的方程的根的情况是( )
A. 无实数根 B. 有两个相等实数根
C. 有两个没有等的正实数根 D. 有两个异号实数根
5. 函数y=ax+b和反比例函数y=在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( )
A. B. C. D.
6. 如图,将等边△ABC的边AC逐渐变成以B为圆心、BA为半径的,长度没有变,AB、BC的长度也没有变,则∠ABC的度数大小由60°变为( )
A. ()° B. ()° C. ()° D. ()°
二、填 空 题(第7—9题,每空1分;第10—16题,每空2分;共23分)
7. 抛物线的开口向__________,顶点坐标是__________,对称轴是__________,函数的最___________值是___________.
8. 某班七个合作学习小组人数为、、、、、、,已知这组数据的平均数是,则这组数据的中位数是____________,众数是____________.
9. 设、是方程的两个根,且,则___________,___________.
10. 已知点,,在函数的图像上,试确定,,的大小关系是___________.
11. 如图,济南建邦大桥有一段抛物线型拱梁,抛物线的表达式为y=ax2+bx.小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶10秒时和26秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC共需_____秒.
12. 如图,扇形AOB的圆心角为122°,C是上一点,则∠ACB=___°.
13. 如图,⊙是等腰直角三角形的内切圆,,,则⊙的半径等于____________.
14. 已知二次函数中,函数与自变量部分对应值如表:
则当时,的取值范围是__________.
15. 一个盒子里有完全相同的三个小球,球上分别标有数字,,,随机摸出一个小球(没有放回),其数字为,再随机摸出另一个小球其数字记为,则满足关于的方程有实数根的概率是___________.
16. 抛物线(a ≠ 0)满足条件:(1);(2);(3)与x轴有两个交点,且两交点间的距离小于2.以下有四个结论:①;②;③;④,其中所有正确结论的序号是_____
三、解 答 题(共85分)
17. 解方程:
();().
18. 作图题:用圆规、直尺作图,没有写作法,但要保留做图痕迹.
已知:线段及.
求作:⊙,使⊙在的内部,,且⊙与的两边分别相切.
19. 在“爱满扬州”慈善一日捐中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成统计图.
(1)这50名同学捐款的众数为 元,中位数为 元;
(2)求这50名同学捐款的平均数;
(3)该校共有600名学生参与捐款,请估计该校学生的捐款总数.
20. 请在网格坐标系中画出二次函数的大致图象(注:图中小正方形网格的边长为),根据图象填空:
()当__________时,有最__________值__________.
()随的增大而减小的自变量的取值范围是__________.
()图象直接写出时的范围:__________.
()图象直接写出时的取值范围:__________.
21. 某景区月日—月日一周天气预报如图,小丽打算选择这期间的或两天去该景区旅游.
()随机选择,恰好天气预报是晴的概率是___________.
()求随机选择连续的两天,恰好天气预报都是晴的概率.
22. 二次函数的图像点.
()求该二次函数的关系式.
()证明:无论取何值,函数值总没有等于.
()将该抛物线先向___________(填“左”或“右”)平移___________个单位,再向___________(填“上”或“下”)平移___________个单位,使得该抛物线的顶点为原点.
23. 如图,已知、与⊙相切于点、,连接并延长交于点.若,.
()求⊙的半径.
()求长.
24. 为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌粽子,每盒进价是40元.超市规定每盒售价没有得少于45元.根据以往发现;当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的量y(盒)与每盒售价x(元)之间的函数关系式;
(2)当每盒售价定为多少元时,每天的利润P(元)?利润是多少?
(3)为稳定物价,有关管理部门限定:这种粽子的每盒售价没有得高于58元.如果超市想要每天获得没有低于6000元的利润,那么超市每天至少粽子多少盒?
25. 如图,在平面直角坐标系中,二次函数的图像与轴交于、两点,与轴交于点,点是抛物线顶点,点是直线下方的抛物线上一动点.
()这个二次函数表达式为____________.
()设直线的解析式为,则没有等式的解集为___________.
()连结、,并把沿翻折,得到四边形,那么是否存在点,使四边形为菱形?若存在,请求出此时点的坐标;若没有存在,请说明理由.
()当四边形的面积时,求出此时点的坐标和四边形的面积.
()若把条件“点是直线下方的抛物线上一动点.”改为“点是抛物线上的任一动点”,其它条件没有变,当以、、、为顶点的四边形为梯形时,直接写出点的坐标.
2022-2023学年江苏省南京市九年级上册数学期末专项提升模拟卷(卷二)
一、选一选(每题2分,共12分)
1. 下列函数解析式中,一定为二次函数的是( )
A. y=3x-1 B. y=ax2+bx+c C. s=2t2-2t+1 D. y=x2+
【正确答案】C
【分析】根据二次函数的定义求解即可.
【详解】解:A、y=3x-1是函数,没有是二次函数,没有符合题意;
B、y=ax2+bx+c,当时,没有是二次函数,没有符合题意;
C、s=2t2-2t+1是二次函数,符合题意;
D、y=x2+ 中没有是整式,故y=x2+ 没有是二次函数,没有符合题意.
故选:C.
此题考查了二次函数的定义,解题的关键是熟练掌握二次函数的定义.二次函数定义:一般地,把形如(a、b、c是常数,且)的函数叫做二次函数,其中a称为二次项系数,b为项系数,c为常数项.x为自变量,y为因变量.
2. 若一组数据2,3,4,5,的方差与另一组数据5,6,7,8,9的方差相等,则的值为( ).
A. 1 B. 6
C 1或6 D. 5或6
【正确答案】C
【分析】根据数据x1,x2,…xn与数据x1+a,x2+a,…xn+a的方差相同这个结论即可解决问题.
【详解】解:∵一组数据2,2,4,5,x的方差与另一组数据5,6,7,8,9的方差相等,
∴这组数据可能是2,3,4,5,6或1,2,3,4,5,
∴x=1或6,
故选:C
本题考查方差、平均数等知识,解题的关键结论:数据x1,x2,…xn与数据x1+a,x2+a,…xn+a的方差相同解决问题.
3. 下列表格是二次函数的自变量与函数值的对应值,判断方程(,,,为常数)的一个解得范围是( )
A. B.
C. D.
【正确答案】B
【详解】解:函数y=ax2+bx+c的图象与x轴的交点就是方程ax2+bx+c=0的根,函数y=ax2+bx+c的图象与x轴的交点的纵坐标为0;
由表中数据可知:y=0在y=﹣0.01与y=0.02之间,∴对应的x的值在﹣2.13与﹣2.12之间,即﹣2.13<x1<﹣2.12.故选B.
4. 已知函数图象如图,那么关于的方程的根的情况是( )
A. 无实数根 B. 有两个相等实数根
C. 有两个没有等的正实数根 D. 有两个异号实数根
【正确答案】C
【分析】根据抛物线的顶点坐标的纵坐标为-3,判断方程的根的情况即是判断y=-2时x的值.
【详解】∵的图象与x轴有两个交点,顶点坐标的纵坐标是−3,
∵方程,
∴时,即是y=−2求x的值,
由图象可知:有两个同号没有等实数根,
故答案为C.
此题考查抛物线与坐标轴的交点,解题关键在于图象判断实数根个数.
5. 函数y=ax+b和反比例函数y=在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( )
A. B. C. D.
【正确答案】C
【详解】解:由图可知:,所以,二次函数y=ax2+bx+c的图象开口向下,排除D,由c>0,排除A,对称轴>0,所以,排除B,
故选:C.
本题考查函数、二次函数、反比函数的图象及其性质.
6. 如图,将等边△ABC的边AC逐渐变成以B为圆心、BA为半径的,长度没有变,AB、BC的长度也没有变,则∠ABC的度数大小由60°变为( )
A. ()° B. ()° C. ()° D. ()°
【正确答案】D
【分析】设∠ABC的度数为n,根据弧长的计算公式把已知条件代入计算即可.
【详解】解:设∠ABC的度数大小由60变为n,
则AC=,由AC=AB,
解得n=
故选D.
本题考查的是弧长的计算和等边三角形的性质,掌握弧长的计算公式l=是解题的关键.
二、填 空 题(第7—9题,每空1分;第10—16题,每空2分;共23分)
7. 抛物线的开口向__________,顶点坐标是__________,对称轴是__________,函数的最___________值是___________.
【正确答案】 ①. 下, ②. (3,1), ③. 直线x=3, ④. 大, ⑤. 1.
【详解】解:∵y=﹣2(x﹣3)2+1,二次项系数为﹣2<0,∴抛物线开口向下,对称轴为直线x=3,顶点坐标为(3,1),函数有值,为1.故答案为向下,(3,1),直线x=3,大,1.
8. 某班七个合作学习小组人数为、、、、、、,已知这组数据的平均数是,则这组数据的中位数是____________,众数是____________.
【正确答案】 ①. 6, ②. 5或7.
【详解】解:∵4、5、5、x、7、7、8的平均数是6,∴(4+5+5+x+7+7+8)÷7=6,解得:x=6,将这组数据从小到大排列为4、5、5、6、7、7、8,最中间的数是6,则这组数据的中位数是6; 5和7都出现了2次,出现的次数至多,则众数是5和7.故答案为6;5或7.
点睛:本题考查了众数与中位数,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数,如果中位数的概念掌握得没有好,没有把数据按要求重新排列,就会出错;众数是一组数据中出现次数至多的数.
9. 设、是方程的两个根,且,则___________,___________.
【正确答案】4,3
【详解】解:由韦达定理,得:.∵,∴,∴.故答案为4,3.
10. 已知点,,在函数的图像上,试确定,,的大小关系是___________.
【正确答案】.
【详解】解:∵函数y=2(x+1)2﹣0.5的图象开口向上,对称轴为直线x=﹣1,∴在对称轴的左侧,y随x增大而减小.∵对称轴为直线x=﹣1,∴A(1,y1)关于对称轴的对称点为A′(-3,y1).∵-3<-2<﹣<﹣1,∴y1>y3 >y2.故答案为 y1>y3 >y2.
11. 如图,济南建邦大桥有一段抛物线型的拱梁,抛物线的表达式为y=ax2+bx.小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶10秒时和26秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC共需_____秒.
【正确答案】36.
【详解】设在10秒时到达A点,在26秒时到达B,
∵10秒时和26秒时拱梁的高度相同,
∴A,B关于对称轴对称.
则从A到B需要16秒,从A到D需要8秒.
∴从O到D需要10+8=18秒.∴从O到C需要2×18=36秒.
12. 如图,扇形AOB的圆心角为122°,C是上一点,则∠ACB=___°.
【正确答案】119
【分析】在⊙O上取点D,连接AD,BD,根据同弧所对的圆周角是圆心角的一半,即可求出∠ADB的度数;又因为四边形ADBC是圆内接四边形,可知圆内接四边形对角互补,据此进行求解即可.
【详解】如图所示,在⊙O上取点D,连接AD,BD,
∵∠AOB=122°,
∴∠ADB=∠AOB=×122°=61°,
∵四边形ADBC是圆内接四边形,
∴∠ACB=180°-61°=119°.
故答案为119.
本题考查的是圆周角定理以及圆内接四边形的性质,作出正确的辅助线是解题关键.
13. 如图,⊙是等腰直角三角形的内切圆,,,则⊙的半径等于____________.
【正确答案】.
【详解】解:设⊙O与等腰直角三角形相切于E、F、G,连接OE、OF,∴∠CEO=∠CFO=90°.又∵∠C=90°,OE=OF,∴四边形CEOF是正方形,设⊙O的半径为r,∴CE=CF=r,∴AE=BF=4﹣r,由切线长定理可得:AG=AE=4﹣r,BG=BF=4﹣r,由勾股定理可得:AB=,∴AG+BG=AB,∴4﹣r+4﹣r=,∴r=.故答案为.
点睛:本题考查了三角形内切圆的性质,涉及等腰三角形的性质,正方形的判定与性质,勾股定理、切线长定理等知识,综合程度较高,属于中等题型.
14. 已知二次函数中,函数与自变量的部分对应值如表:
则当时,的取值范围是__________.
【正确答案】.
【详解】解:由表可知,二次函数对称轴为直线x=2,所以,当x=4时,y=5,当y<5时,x的取值范围为0<x<4.故答案为0<x<4.
点睛:本题考查了二次函数与没有等式,观察图表得到y=5的另一个x的值是解题的关键.
15. 一个盒子里有完全相同的三个小球,球上分别标有数字,,,随机摸出一个小球(没有放回),其数字为,再随机摸出另一个小球其数字记为,则满足关于的方程有实数根的概率是___________.
【正确答案】.
【详解】解:画树状图得:
∵共有6种等可能的结果,满足关于x的方程x2+px+q=0有实数根的有4种情况,∴满足关于x的方程x2+px+q=0有实数根的概率是:.故答案为.
16. 抛物线(a ≠ 0)满足条件:(1);(2);(3)与x轴有两个交点,且两交点间的距离小于2.以下有四个结论:①;②;③;④,其中所有正确结论的序号是_____
【正确答案】②④
【详解】∵4a-b=0,
∴抛物线的对称轴为x=-=-2
∵a-b+c>0,
∴当x=-1时,y>0,
∵抛物线与x轴有两个没有同的交点且这两个交点之间的距离小于2,
∴抛物线与x轴的两个交点的横坐标位于-3与-1之间,b2-4ac>0
∴16a2-4ac=4a(4a-c)>0,据条件得图象:
∴a>0,b>0,c>0,
∴4a-c>0,∴4a>c即a>,
∵当x=-3时,9a-3b+c>0,由b=4a,
∴c>3a即a<,
∴<a< ,
当x=1时,y=a+b+c>0.
故答案为②④.
三、解 答 题(共85分)
17. 解方程:
();().
【正确答案】(1);(2),.
【详解】试题分析:(1)用因式分解法求解可得;
(2)用因式分解法求解可得.
试题解析:解:(1)∵(x﹣)2=0,∴x﹣=0,∴;
(2)∵(x+1)(x﹣1)﹣2(x+1)=0,∴(x+1)(x﹣1﹣2)=0,即(x+1)(x﹣3)=0,则x+1=0或x﹣3=0,解得:,.
点睛:本题主要考查了解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,方程的特点选择合适、简便的方法是解题的关键.
18. 作图题:用圆规、直尺作图,没有写作法,但要保留做图痕迹.
已知:线段及.
求作:⊙,使⊙在的内部,,且⊙与的两边分别相切.
【正确答案】答案见解析.
【详解】试题分析:①作∠ACB的平分线CM,在射线CM上截取CO=a,②作ON⊥CB交CB于K,③以C为圆心,OK为半径作⊙O.⊙O即为所求.
试题解析:解:如图,①作∠ACB的平分线CM,在射线CM上截取CO=a,②作ON⊥CB交CB于K,③以C为圆心,OK为半径作⊙O.
⊙O即为所求.
19. 在“爱满扬州”慈善一日捐中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成统计图.
(1)这50名同学捐款的众数为 元,中位数为 元;
(2)求这50名同学捐款的平均数;
(3)该校共有600名学生参与捐款,请估计该校学生的捐款总数.
【正确答案】(1)15,15;(2)13(元);(3)7800(元).
【详解】试题分析:(1)根据众数的定义即出现次数至多的数据进而得出即可,再利用中位数的定义得出即可;
(2)利用条形统计图得出各组频数,再根据加权平均数的公式计算即可;
(3)利用样本估计总体的思想,用总数乘以捐款平均数即可得到捐款总数.
解:(1)数据15元出现了20次,出现次数至多,所以众数是15元;
数据总数为50,所以中位数是第25、26位数的平均数,即(15+15)÷2=15(元).
故答案为15,15;
(2)50名同学捐款的平均数=(5×8+10×14+15×20+20×6+25×2)÷50=13(元);
(3)估计这个中学的捐款总数=600×13=7800(元).
考点:条形统计图;用样本估计总体;加权平均数;中位数;众数.
20. 请在网格坐标系中画出二次函数的大致图象(注:图中小正方形网格的边长为),根据图象填空:
()当__________时,有最__________值__________.
()随的增大而减小的自变量的取值范围是__________.
()图象直接写出时的范围:__________.
()图象直接写出时的取值范围:__________.
【正确答案】(1)2,小,-3;(2)x<2;(3)-3≤y<13;(4)0≤x≤4.
【详解】试题分析:画出二次函数的图象,根据图象即可得到结论.
试题解析:解:二次函数y=x2﹣4x+1的大致图象如图所示:
(1)由图象知:当x=2时,y有最小值=﹣3.故答案为2,小,﹣3;
(2)∵抛物线的对称轴为直线x=2,∴y随x的增大而减小的自变量x的取值范围是:x<2.故答案为x<2;
(3)由图象知:当﹣2<x<4时y的范围:﹣3≤y<13.故答案为﹣3≤y<13;
(4)当y≤1时x的取值范围为:0≤x≤4.故答案为0≤x≤4.
点睛:本题考查了二次函数的图象与性质,二次函数的最值以及二次函数和没有等式的关系.数形思想的运用是解答本题的关键.
21. 某景区月日—月日一周天气预报如图,小丽打算选择这期间的或两天去该景区旅游.
()随机选择,恰好天气预报是晴的概率是___________.
()求随机选择连续的两天,恰好天气预报都是晴的概率.
【正确答案】(1);(2).
【详解】试题分析:(1)由天气预报是晴的有4天,直接利用概率公式求解即可求得答案;
(2)首先利用列举法可得:随机选择连续的两天等可能的结果有:晴晴,晴雨,雨阴,阴晴,晴晴,晴阴,然后直接利用概率公式求解即可求得答案.
试题解析:解:(1)∵天气预报是晴的有4天,∴随机选择,恰好天气预报是晴的概率为:;
(2)∵随机选择连续的两天等可能的结果有:晴晴,晴雨,雨阴,阴晴,晴晴,晴阴,∴随机选择连续的两天,恰好天气预报都是晴的概率为:=.
22. 二次函数的图像点.
()求该二次函数的关系式.
()证明:无论取何值,函数值总没有等于.
()将该抛物线先向___________(填“左”或“右”)平移___________个单位,再向___________(填“上”或“下”)平移___________个单位,使得该抛物线的顶点为原点.
【正确答案】(1);(2)答案见解析;(3)左,1,下,2.
【详解】试题分析:(1)直接将(3,6)点代入即可求出a的值;
(2)直接利用配方法求出二次函数最值进而得出判断即可;
(3)直接利用二次函数平移规律得出答案.
试题解析:(1)解:将(3,6)代入y=ax2﹣2x+3得:
6=9a﹣6+3,解得:a=1,故抛物线解析式为:y=x2﹣2x+3;
(2)证明:∵y=x2﹣2x+3=(x﹣1)2+2,∴函数值y有最小值2,故无论x取何值,函数值y总没有等于1;
(3)解:将该抛物线先向左平移1单位,得到y=x2+2,再向下平移2个单位,得到y=x2,该抛物线的顶点为原点.
故答案为左,1,下,2.
点睛:本题主要考查了待定系数法求二次函数解析式以及配方法求二次函数最值以及二次函数的平移,正确记忆平移规律是解题的关键.
23. 如图,已知、与⊙相切于点、,连接并延长交于点.若,.
()求⊙的半径.
()求长.
【正确答案】(1)3;(2).
【详解】试题分析:(1)连接半径OA,在Rt△OCD中,根据勾股定理列方程可求得r的值;
(2)由垂直平分线的逆定理得:OA是BC的中垂线,根据垂径定理得:BE=CE,利用面积法列式可求得BE的长,由BC=2BE即可得到结论.
试题解析:解:(1)连接OC.∵AB、AC是⊙O的切线,∴AB=AC=6,OC⊥AD,BD⊥AB,∴∠ABD=∠OCD=90°,在Rt△ABD中,由勾股定理得:AD==10,∴CD=10﹣6=4.∵⊙O的半径r,∴OB=OC=r,OD=8﹣r,在Rt△OCD中,(8﹣r)2=r2+42,64﹣16r=16,∴r=3;
(2)连接OA,交BC于E.∵AB=AC,OB=OC,∴OA是BC的中垂线,∴BE=CE,在Rt△ABO中,AO==,∴S△ABO=AB•OB=OA•BE,6×3=BE,∴BE=,∴BC=2BE=.
点睛:本题考查了切线长定理、线段垂直平分线的逆定理、勾股定理,熟练掌握切线长定理是本题的关键,在圆中的计算题中,常设半径为r,根据勾股定理列方程解决问题.
24. 为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌粽子,每盒进价是40元.超市规定每盒售价没有得少于45元.根据以往发现;当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天量y(盒)与每盒售价x(元)之间的函数关系式;
(2)当每盒售价定为多少元时,每天的利润P(元)?利润是多少?
(3)为稳定物价,有关管理部门限定:这种粽子的每盒售价没有得高于58元.如果超市想要每天获得没有低于6000元的利润,那么超市每天至少粽子多少盒?
【正确答案】(1)y=﹣20x+1600;
(2)当每盒售价定为60元时,每天的利润P(元),利润是8000元;
(3)超市每天至少粽子440盒.
【详解】试题分析:(1)根据“当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒”即可得出每天的量y(盒)与每盒售价x(元)之间的函数关系式;
(2)根据利润=1盒粽子所获得的利润×量列式整理,再根据二次函数的最值问题解答;
(3)先由(2)中所求得的P与x的函数关系式,根据这种粽子的每盒售价没有得高于58元,且每天粽子的利润没有低于6000元,求出x的取值范围,再根据(1)中所求得的量y(盒)与每盒售价x(元)之间的函数关系式即可求解.
试题解析:(1)由题意得,==;
(2)P===,∵x≥45,a=﹣20<0,∴当x=60时,P值=8000元,即当每盒售价定为60元时,每天的利润P(元),利润是8000元;
(3)由题意,得=6000,解得,,∵抛物线P=的开口向下,∴当50≤x≤70时,每天粽子的利润没有低于6000元的利润,又∵x≤58,∴50≤x≤58,∵在中,<0,∴y随x的增大而减小,∴当x=58时,y最小值=﹣20×58+1600=440,即超市每天至少粽子440盒.
考点:二次函数的应用.
25. 如图,在平面直角坐标系中,二次函数的图像与轴交于、两点,与轴交于点,点是抛物线顶点,点是直线下方的抛物线上一动点.
()这个二次函数的表达式为____________.
()设直线的解析式为,则没有等式的解集为___________.
()连结、,并把沿翻折,得到四边形,那么是否存在点,使四边形为菱形?若存在,请求出此时点的坐标;若没有存在,请说明理由.
()当四边形的面积时,求出此时点的坐标和四边形的面积.
()若把条件“点是直线下方的抛物线上一动点.”改为“点是抛物线上的任一动点”,其它条件没有变,当以、、、为顶点的四边形为梯形时,直接写出点的坐标.
【正确答案】(1);(2)x≤0或x≥3;(3);(4)当P时,S四边形ABPC;(5)点P的坐标为(-2,5),(2,-3)或(4,5).
【详解】试题分析:(1)直接设成顶点式即可得出抛物线解析式;
(2)先确定出点B,C坐标,再根据图象直接写出范围;
(3)利用菱形的性质得出PO=PC即可得出点P的纵坐标,代入抛物线解析式即可得出结论;
(4)先利用坐标系中几何图形的面积的计算方法建立函数关系式即可求出面积的值;
(5)先求出直线BC,BC,CD的解析式,分三种情况利用梯形的性质,一组对边平行即可得出直线DP1,CP2,BP3的解析式,分别联立抛物线的解析式建立方程组求解即可.
试题解析:解:(1)∵点D(1,﹣4)是抛物线y=x2+bx+c的顶点,∴y=(x﹣1)2﹣4=x2﹣2x﹣3.故答案为y=x2﹣2x﹣3;
(2)令x=0,∴y=﹣3,∴C(0,﹣3),令y=0,∴x2﹣2x﹣3=0,∴x=﹣1或x=3,∴A(﹣1,0),B(3,0),∴没有等式x2+bx+c≥kx+m的解集为x<0或>3.故答案为x<0或>3;
(3)如图1.∵四边形POP′C为菱形,∴PO=PC.∵C(0,﹣3),∴点P的纵坐标为﹣.∵P在抛物线y=x2﹣2x﹣3上,∴﹣=x2﹣2x﹣3,∴x=或x=(舍),∴P(.﹣);
(4)如图2,由(1)知,B(3,0),C(0,﹣3),∴直线BC的解析式为y=x﹣3,过点P作PE∥y轴交BC于E,设P(m,m2﹣2m﹣3),(0<m<3)
∴E(m,m﹣3),∴PE=m﹣3﹣(m2﹣2m﹣3)=﹣m2+3m.∵A(﹣1,0),B(3,0),C(0,﹣3),∴S四边形ABPC=S△ABC+S△PCE+S△PBE=AB•OC+PE•|xP|+PE•|xB﹣xP|
=AB•OC+PE(|xP|+|xB﹣xP|)=×4×3+(﹣m2+3m)×(m+3﹣m)
=6+×(﹣m2+3m)=﹣(m﹣)2+
当m=时,S四边形ABPC=.
当m=时,m2﹣2m﹣3=,∴P.
(5)如图,由(1)知,B(3,0),C(0,﹣3),D(1,﹣4),∴直线BC的解析式为y=x﹣3,直线BD的解析式为y=2x﹣6,直线CD的解析式为y=﹣x﹣3.∵以P、C、D、B为顶点的四边形为梯形.∵抛物线的解析式为y=x2﹣2x﹣3①;
①当DP1∥BC时,∴直线DP1的解析式为y=x﹣5②,联立①②解得,点P1(2,﹣3),[另一个点为(1,﹣4)和点D重合,舍去]
②当CP2∥BD时,∴直线CP2的解析式为y=2x﹣3③,联立①③解得点P2(4,5)
③当BP3∥CD时,∴直线BP3∥CD的解析式为y=﹣x+3④,联立①④解得点P3(﹣2,5).
综上所述:以P、C、D、B为顶点的四边形为梯形时,点P的坐标为(﹣2,5)、(2,﹣3)或(4,5).
点睛:本题是二次函数综合题,主要考查了待定系数法求抛物线解析式,没有规则图形的面积的计算方法,菱形的性质,梯形的性质,解答本题的关键是用方程或方程组的思想解决问题.
2022-2023学年江苏省南京市九年级上册数学月考专项提升模拟卷(AB卷)含解析: 这是一份2022-2023学年江苏省南京市九年级上册数学月考专项提升模拟卷(AB卷)含解析,共55页。试卷主要包含了选一选,填 空 题,解 答 题等内容,欢迎下载使用。
2022-2023学年广东省深圳市九年级上册数学期末专项提升模拟卷(卷一卷二)含解析: 这是一份2022-2023学年广东省深圳市九年级上册数学期末专项提升模拟卷(卷一卷二)含解析,共54页。试卷主要包含了选一选,填 空 题,解 答 题等内容,欢迎下载使用。
2022-2023学年广东省广州市九年级上册数学期末专项提升模拟卷(卷一卷二)含解析: 这是一份2022-2023学年广东省广州市九年级上册数学期末专项提升模拟卷(卷一卷二)含解析,共50页。试卷主要包含了选一选,填 空 题,解 答 题等内容,欢迎下载使用。












