初中12.2 三角形全等的判定一课一练

这是一份初中12.2 三角形全等的判定一课一练，共18页。
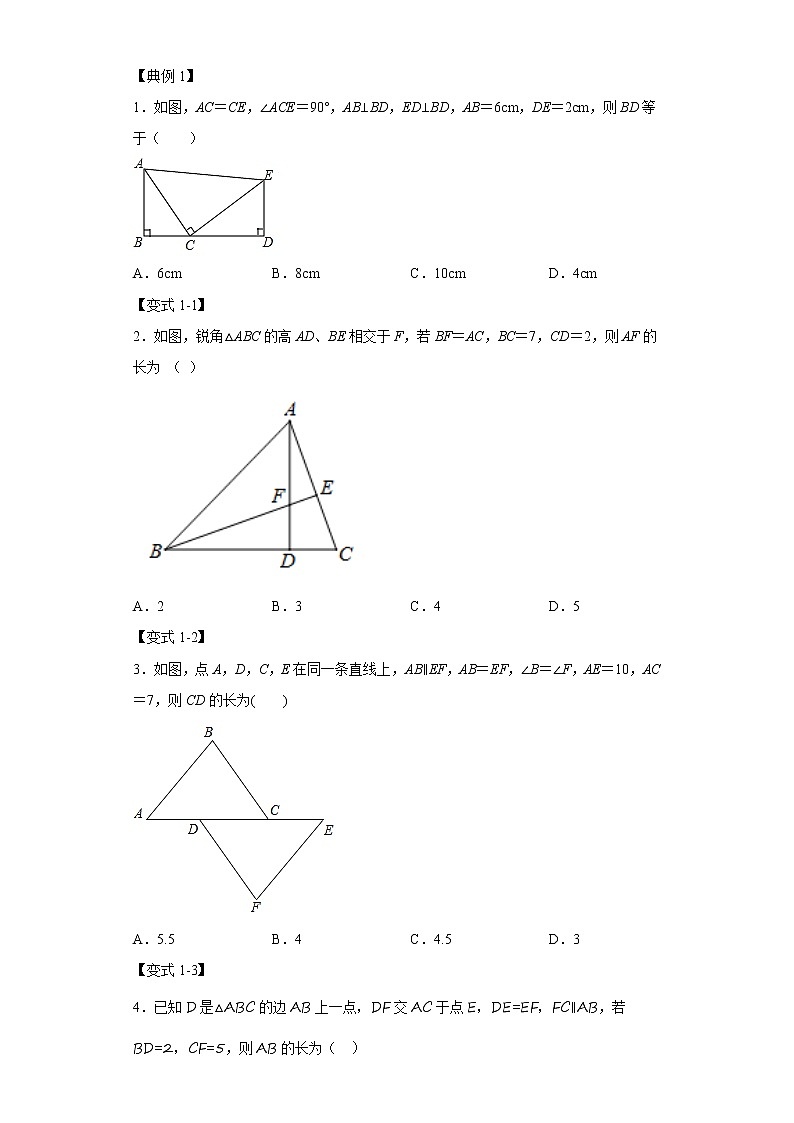
专题12.3 全等三角形性质与判定（知识解读）-2022-2023学年八年级数学上册《同步考点解读·专题训练》（人教版）【直击考点】【学习目标】1. 掌握根据题目选会用“SSS”、“SAS”、“ASA”、“AAS”和“斜边、直角边”条件判定两个三角形全等. 2. 能够运用全等三角形的性质作答；【知识点梳理】考点 1  全等三角形性质与判定全等三角形的性质：1.两全等三角形的对应边相等，对应角相等.2.全等三角形的对应边上的高相等，对应边上的中线相等，对应角的平分线相等.3.全等三角形的周长、面积相等.全等三角形的判定考点 1  全等三角形的应用【典例分析】【考点1 全等角形的性质与判定】【典例1】1．如图，AC＝CE，∠ACE＝90°，AB⊥BD，ED⊥BD，AB＝6cm，DE＝2cm，则BD等于（　　）A．6cm B．8cm C．10cm D．4cm【变式1-1】2．如图，锐角△ABC的高AD、BE相交于F，若BF＝AC，BC＝7，CD＝2，则AF的长为 （ ）A．2 B．3 C．4 D．5【变式1-2】3．如图，点A，D，C，E在同一条直线上，AB∥EF，AB＝EF，∠B＝∠F，AE＝10，AC＝7，则CD的长为(　　)A．5.5 B．4 C．4.5 D．3【变式1-3】4．已知D是△ABC的边AB上一点，DF交AC于点E，DE=EF，FC∥AB，若BD=2，CF=5，则AB的长为（    ）A．1 B．3 C．5 D．7【典例2】5．如图，AB＝AC，AD＝AE，∠BAC＝∠DAE．（1）求证：△ABD≌△ACE；（2）若∠1＝25°，∠2＝30°，求∠3的度数．【变式2-1】6．如图，点D，E分别在AC，AB上，，．(1)求证：．(2)若，，求的度数．【变式2-2】7．如图，在△ABC和△AEF中，点E在BC边上，AE＝AB，AC＝AF，∠CAF＝∠BAE，EF与AC交于点G．(1)求证：EF＝BC；(2)若∠B＝62°，∠ACB＝24°，求∠FGC的度数．【典例3】8．如图，M是线段AB上的一点，ED是过点M的一条线段，连接AE、BD，过点B作BF∥AE交ED于点F，且EM＝FM．（1）求证：AE＝BF．（2）连接AC，若∠AEC＝90°，∠CAE=∠DBF，CD＝4，求EM的长．【变式3-1】9．如图，中，AD是BC边上的中线，E，F为直线AD上的点，连接BE，CF，且．(1)求证：≌；(2)若，，试求DE的长．【变式3-2】10．如图，在△ABC中，AB=AC，点D在BC边上，点E在AC边上，连接AD，DE．已知∠1=∠2，AD=DE．(1)求证：△ABD≌△DCE；(2)若BD=3，CD=5，求AE的长．【变式3-3】11．如图，在△ABC中，D是边AB上一点，E是边AC的中点，过点C作交DE的延长线于点F．（1）求证：△ADE≌△CFE；（2）若AB＝AC，CE＝5，CF＝7，求DB的长．【考点2 全等角形的应用】【典例4】12．一块三角形玻璃不慎被小明摔成了四片碎片（如图所示），小明经过仔细的考虑认为只要带其中的两块碎片去玻璃店，就可以让师傅配一块与原玻璃一样的玻璃．你认为下列四个答案中考虑最全面的是（　　）A．带其中的任意两块去都可以 B．带1、4或2、3去就可以了C．带1、4或3、4去就可以了 D．带1、2或2、4去就可以了【变式4-1】13．如图，把两根钢条的中点连在一起，可以做成一个测量工件内槽宽的工具（卡钳）．在图中，要测量工件内槽宽AB，只要测量A′B′就可以，这是利用什么数学原理呢？（    ）A．AAS B．SAS C．ASA D．SSS【变式4-2】14．如图，要测池塘两端A，B的距离，小明先在地上取一个可以直接到达A和B的点C，连接AC并延长到D，使CD＝CA；连接BC并延长到E，使CE＝CB，发现DE＝AB．那么判定△ABC和△DEC全等的依据是（    ）A．SSS B．SAS C．ASA D．AAS【变式4-3】15．小明在学习了全等三角形的相关知识后，发现了一种测量距离的方法．如图，小明直立在河岸边的处，他压低帽子帽沿，使视线通过帽沿，恰好落在河对岸的处，然后转过身，保持和刚才完全一样的姿势，这时视线落在水平地面的处（，，三点在同一水平直线上），小明通过测量，之间的距离，即得到，之间的距离．小明这种方法的原理是（    ）A． B． C． D．【变式4-4】16．工人师傅常用角尺平分一个任意角，做法如下：如图，是一个任意角，在边，上分别取，移动角尺，使角尺两边相同的刻度分别与，重合．过角尺顶点作射线．由此做法得的依据是（  ）A． B． C． D．【典例5】17．李华同学用11块高度都是1cm的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个正方形ABCD（∠ABC＝90°，AB＝BC），点B在EF上，点A和C分别与木墙的顶端重合，求两堵木墙之间的距离EF．【变式5-1】18．小明沿一段笔直的人行道行走，边走边欣赏风景，在由处走向处的过程中，通过隔离带的缝隙，刚好浏览完对面人行道宣传墙上的一条标语，具体信息如下：如图，，相邻两平行线间的距离相等，，相交于点，，垂足为．小明根据自己步行的路程长为，测出标语的长度也为，请说明理由．   
参考答案：1．B【分析】根据题意证明即可得出结论．【详解】解：∵AB⊥BD，ED⊥BD，∴，∵∠ACE＝90°，∴，∵，∴，在和中，，∴，∴，，∴，故选：B．【点睛】本题考查了全等三角形的判定与性质，熟练掌握全等三角形的判定定理以及性质定理是解本题的关键．2．B【详解】解：∵AD、BE是锐角△ABC的高，∴∠BDF=∠ADC=90°∴∠DBF=90°-∠C ，∠DAC=90°-∠C ， ∴∠DBF=∠DAC∵BF=AC，∴△BDF≌△ADC∴BD=AD，DF=CD∵BD=BC-CD=5∴AD=5∴AF=AD-DF=AD-CD=3故选∶B3．B【详解】解：因为AB∥EF，所以∠A=∠E，又AB=EF，∠B=∠F，所以△ABC≌△EFD，所以AC= ED =7，又AE=10，所以CE=3，所以CD=ED-CE=7-3=4，故选B．4．D【分析】根据FC∥AB，得出∠ADE=∠CFE，然后联立∠AED=∠CEF及DE=EF，从而根据AAS来判定△ADE≌△CFE；接下来根据全等三角形的性质可得：AD=CF=5，则AB=AD+BD，即可求出AB的长度.【详解】∵FC∥AB，∴∠ADE=∠CFE.∵在△ADE和△CFE中，∠ADE=∠CFE，DE=FE，∠AED=∠CEF，∴△ADE≌△CFE，∴AD=CF=5，∴AB=AD+BD=2+5=7.故选D.【点睛】本题考查了全等三角形的判定和性质、平行线的性质，解决本题的关键是求证△ADE≌△CFE.5．（1）见解析；（2）∠3＝55°．【分析】（1）先由∠BAC=∠DAE，就可以得出∠1＝∠EAC，就可以得出△ABD≌△ACE；（2）由（1）得出∠ABD=∠2，就可以由三角形的外角与内角的关系求出结论．【详解】（1）证明：∵∠BAC＝∠DAE，∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，∴∠1＝∠EAC，在△ABD和△ACE中，，∴△ABD≌△ACE（SAS）；（2）解：∵△ABD≌△ACE，∴∠ABD＝∠2＝30°，∵∠1＝25°，∴∠3＝∠1+∠ABD＝25°+30°＝55°．【点睛】此题考查全等三角形的判定与性质，三角形的外角和与内角和，解题关键在于掌握判定定理.6．(1)见解析(2)65° 【分析】（1）根据，，可得AB=AC，可证得△ABD≌△ACE，即可求证；（2）根据△ABD≌△ACE，可得∠B=∠C=30°，从而得到∠ADB=95°，再由三角形外角的性质，即可求解．（1）证明：∵，．∴AD+CD=AE+BE，即AB=AC，在△ABD和△ACE中，∵AD=AE，∠A=∠A，AB=AC，∴△ABD≌△ACE（SAS），∴BD=CE；（2）解：∵△ABD≌△ACE，，∴∠B=∠C=30°，∵，∴∠ADB=180°-∠A-∠B=95°，∵∠ADB=∠C+∠COD，∴∠COD=65°．【点睛】本题主要考查了全等三角形的判定和性质，三角形外角的性质，三角形内角和定理，熟练掌握全等三角形的判定和性质，三角形外角的性质，三角形内角和定理，是解题的关键．7．(1)证明见解析；(2)∠FGC＝80° 【分析】（1）先证△BAC≌△EAF（SAS），即可求解；（2）根据三角形的内角和定理，补角的概念即可求解；（1）证明：∵∠CAF＝∠BAE，∴∠CAF+∠EAC＝∠BAE+∠EAC，即∠BAC＝∠EAF，在△BAC和△EAF中，，∴△BAC≌△EAF（SAS），∴EF＝BC．（2）解：∵AB＝AE，∴∠B＝∠AEB＝62°，∴∠BAE＝56°，∴∠CAF＝∠BAE＝56°，∵△BAC≌△EAF，∴∠F＝∠C＝24°，∴∠FGC＝∠FAC+∠F＝56°+24°＝80°．【点睛】本题主要考查三角形全等证明，三角形内角和定理，补角的概念，掌握相关知识并灵活应用是解题的关键．8．（1）见解析；（2）2【分析】（1）根据平行线的性质和全等三角形的判定证明△AME≌△BMF即可证得结论；（2）由△AME≌△BMF证得AE=BF，EM=FM，∠BFM=∠AEC=90°，根据全等三角形的判定证明△AEC≌△BFD，则有EC=FD，即EF=CD=4，即可求解．【详解】解：（1）∵BF∥AE，∴∠EAM＝∠FBM，又∠AME＝∠BMF，EM＝FM，∴△AME≌△BMF（ASA），∴AE=BF；（2）∵△AME≌△BMF，∴AE=BF，EM=FM，∠BFM=∠AEC=90°，∴∠AEC=∠BFD=90°，又∠CAE=∠DBF，∴△AEC≌△BFD（ASA），∴EC=FD，即EF=CD=4，∴EM= EF=2．【点睛】本题考查平行线的性质、全等三角形的判定与性质，熟练掌握全等三角形的判定与性质是解答的关键．9．(1)见解析；(2)； 【分析】（1）根据两直线平行内错角相等；全等三角形的判定（角角边）；即可证明；（2）由（1）结论计算线段差即可解答；（1）证明：∵BE∥CF，∴∠BED=∠CFD，∵∠BDE=∠CDF，BD=CD，∴△BDE≌△CDF（AAS）；（2）解：由（1）结论可得DE=DF，∵EF=AE-AF=15-8=7，∴DE=；【点睛】本题考查了平行线的性质，全等三角形的判定（AAS）和性质；掌握全等三角形的判定和性质是解题关键．10．(1)见解析(2)2 【分析】（1）根据AAS可证明△ABD≌△DCE；（2）得出AB = DC = 5，CE= BD= 3，求出AC = 5，则AE可求出．（1）证明：∵AB=AC， ∴∠B=∠C．∵∠1=∠2，AD=DE，∴△ABD≌△DCE．（2）解：∵△ABD≌△DCE∴DB=EC=3，CD=AB=AC=5．∴AE=2．【点睛】本题考查了全等三角形的判定与性质，等腰三角形的性质，熟练掌握全等三角形的判定方法是解题的关键．11．（1）见解析；（2）DB=3．【分析】（1）先证明 再证明从而可得结论；（2）利用全等三角形的性质证明再求解 从而可得答案.【详解】证明：（1） E是边AC的中点， △ADE≌△CFE；（2） △ADE≌△CFE，CE＝5，CF＝7， AB＝AC， 【点睛】本题考查的是全等三角形的判定与性质，掌握“利用证明三角形全等及利用全等三角形的性质求解线段的长度”是解本题的关键.12．C【分析】带1、3去，只有两角，没有完整边不能确定三角形，带1、2或2、3去，只有一角，没有完整边，不能确定三角形，带2、4去，有一角，可以延长边还原出原三角形，带3、4可以用“角边角”确定三角形，带1、4可以用“角边角”确定三角形．即可得出答案【详解】解：带1、3去，只有两角，没有完整边不能确定三角形，带1、2或2、3去，只有一角，不能确定三角形，带2、4去，有一角，可以延长边还原出原三角形，带3、4可以用“角边角”确定三角形，带1、4可以用“角边角”确定三角形，所以A、B、D不符合题意，C符合题，故选：C．【点睛】本题考查了全等三角形判定的应用；确定一个三角形的大小、形状，可以用全等三角形的几种判定方法．做题时要根据实际问题找条件．13．B【分析】根据题意，连接AB，A′B′，证明△AOB≌△A′OB′（SAS）即可求得答案．【详解】解：连接AB，A′B′，如图，∵点O分别是AA′、BB′的中点，∴OA＝OA′，OB＝OB′，在△AOB和△A′OB′中，，∴△AOB≌△A′OB′（SAS）．∴A′B′＝AB．故选：B．【点睛】本题考查了全等三角形的性质与判定，掌握全等三角形的性质与判定是解题的关键．14．B【分析】由题意知AC=DC，BC=EC，由于∠ACB=∠DCE，根据“SAS”即可证明△ABC≌△DEC．【详解】解：由题意知CD=CA，CE=CB，在△DCE和△ABC中，，∴△DCE≌△ABC（SAS）．故选：B．【点睛】此题主要考查了全等三角形的应用，熟练掌握全等三角形判定的“SAS”方法是解题的关键．15．C【分析】根据垂直的定义和全等三角形的判定定理即可得到结论．【详解】小明直立在河岸边的处，说明 保持和刚才完全一样的姿势说明 ∵CO为 与共边．∴与全等的条件为．故选：C．【点睛】本题考查了三角形全等的知识点，掌握该知识点是解答本题的关键．16．D【分析】分析已知条件，找相等的条件进行分析即可作出正确选择．【详解】∵OM=ON，CM=CN，OC为公共边，∴△MOC≌△NOC（SSS）．故选：D．【点睛】此题主要考查学生对全等三角形判定定理的理解和掌握，此题难度不大，属于基础题．17．11cm【分析】根据∠ABE的余角相等求出∠EAB＝∠CBF，然后利用“角角边”证明△ABE和△BCF全等，根据全等三角形对应边相等可得AE＝BF，BE＝CF，于是得到结论．【详解】解：∵AE⊥EF，CF⊥EF，∴∠AEB＝∠BFC＝90°，∴∠EAB+∠ABE＝90°，∵∠ABC＝90°，∴∠ABE+∠CBF＝90°，∴∠EAB＝∠CBF，在△ABE和△BCF中，，∴△ABE≌△BCF（AAS），∴AE＝BF＝5cm，BE＝CF＝6cm，∴EF＝5+6＝11（cm）．【点睛】本题考查了全等三角形的判定和性质，掌握全等三角形的判定方法（即SSS、SAS、ASA、AAS和HL）和全等三角形的性质（即全等三角形的对应边相等、对应角相等）是解题的关键．18．见解析【分析】由AB∥CD，利用平行线的性质可得∠ABP=∠CDP，∠PAB=∠PCD，利用ASA定理可得，△ABP≌△CDP，由全等三角形的性质可得结果．【详解】解：CD=AB=16米，理由如下：∵AB∥CD，∴∠ABP=∠CDP，∵PD⊥CD，∴∠CDP=90°，∴∠ABP=90°，即PB⊥AB，∵相邻两平行线间的距离相等，∴PD=PB，在△ABP与△CDP中，，∴△ABP≌△CDP（ASA），∴CD=AB=16米．【点睛】本题主要考查了平行线的性质和全等三角形的判定及性质定理，利用平行线的性质可得∠ABP=∠CDP，∠PAB=∠PCD是解答此题的关键．