










高中数学人教A版 (2019)必修 第一册3.2 函数的基本性质备课课件ppt
展开第 3章 函数的概念与性质
人教A版2019必修第一册
3.2.1 单调性与最大(小)值—最值(第2课时)
01图像法求函数最值
02利用函数的单调性求最值
目录
03函数单调性的实际应用
04二次函数最值
学习目标
1.理解函数的最大值和最小值的概念及其几何意义.(数学抽象)
2.能借助函数的图象和单调性,求一些简单函数的最值.(数学运算)
3.能利用函数的最值解决有关的实际应用问题.(数学建模)
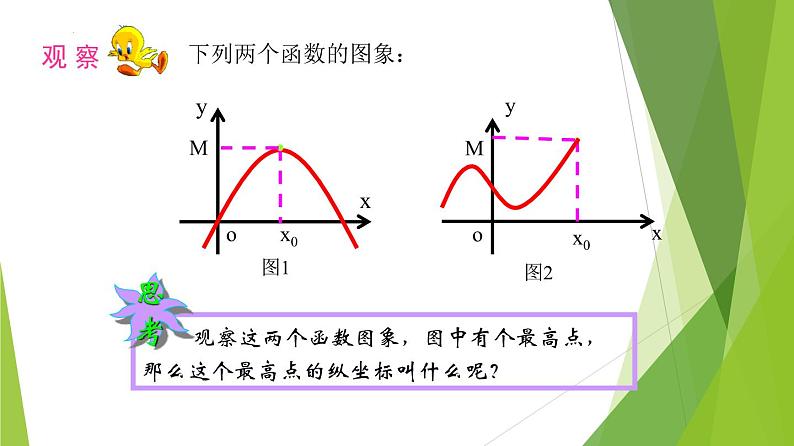
下列两个函数的图象:
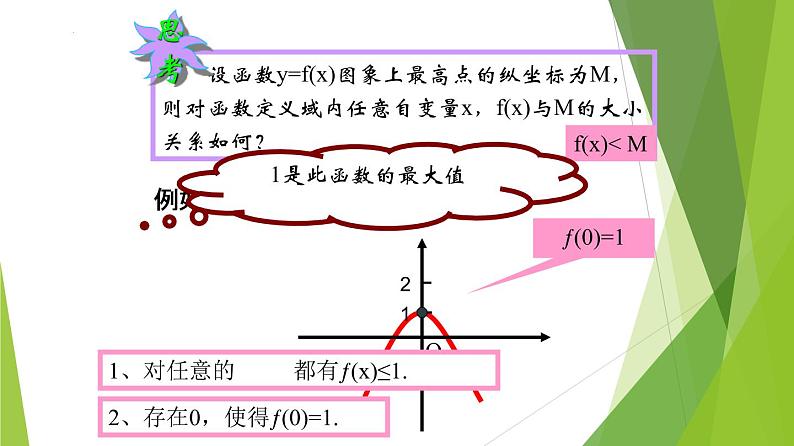
f(x)< M
ƒ(0)=1
2、存在0,使得ƒ(0)=1.
1是此函数的最大值
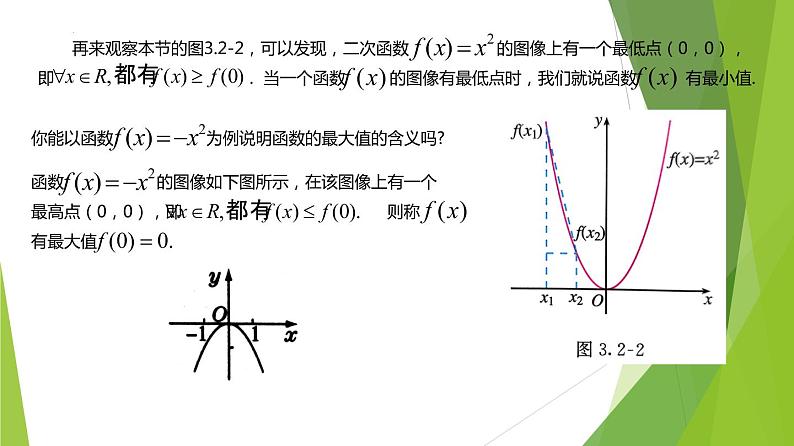
再来观察本节的图3.2-2,可以发现,二次函数 的图像上有一个最低点(0,0),即 . 当一个函数 的图像有最低点时,我们就说函数 有最小值.
你能以函数 为例说明函数的最大值的含义吗?
函数 的图像如下图所示,在该图像上有一个最高点(0,0),即 则称 有最大值
一般地,设函数 的定义域为 I ,如果存在实数M满足:
那么,我们称M是函数 的最大值.
思考:你能仿照函数最大值的定义,给出函数 的最小值的定义吗?
一般地,设函数 的定义域为 I ,如果存在实数M满足:
那么,我们称M是函数 的最小值.
最大值定义
最小值定义
对函数的最值的理解(1)最值首先是一个函数值,即在函数的定义域 I 内,存在在一个自变量 ,使得 等于最值.(2)对于定义域内任何元素 x ,都有 “任意”两个字不可省略.(3)使函数 f(x)取最值的自变量的值有时可能不止一个.(4)函数 f(x)的最大值的几何意义是其图象上最高点的纵坐标;最小值的几何意义是其图象上最低点的纵坐标.
函数的最值与值域的关系(1)函数的最值和值域反应的是函数的整体性质,针对的是整个定义域;(2)函数的值域一定存在,函数的最值不一定存在;(3)若函数的最值存在,则最值一定是值域中的元素;(4)若函数的值域是开区间,则函数无最值;若函数的值域是闭区间,则闭区间的端点值就是函数的最值.
典例1
所以,烟花冲出1.5s是它爆裂的最佳时刻,此时距离地面的高度约为29m.
方法总结 图象法求函数最值的一般步骤
分析:由函数的图象可知道,此函数在[2,6]上递减。所以在区间[2,6]的两个端点上分别取得最大值与最小值.
典例2
(4)若函数定义域为开区间,则不但要考虑函数在该区间上的单调性,还要考虑端点处的函数值或者发展趋势.
(2)工厂生产多少台产品时,可使盈利最多?
典例3
方法总结 (1)解实际应用题时,要弄清题意,从实际出发,引入数学符号,建立数学模型,列出函数关系式,分析函数的性质,从而解决问题,要注意自变量的取值范围.
(2)在实际应用问题中,最大利润、用料最省等问题常转化为求函数最值来解决,本题转化为二次函数求最值,利用配方法和分类讨论思想使问题得到解决.
练一练
练一练
3.将进货单价为40元的商品按50元一个出售时,能卖出500个,已知这种商品每涨价1元,其销售量就减少10个,为得到最大利润,售价应为多少元?最大利润为多少?
练一练
问题1:.如何表示矩形的面积?
问题3:.你能归纳求二次函数最值的方法吗?
[答案] 求解二次函数最值问题的方法:
(1)确定对称轴与抛物线的开口方向并作图.
(2)在图象上标出定义域的位置.
(3)观察函数图象,通过函数的单调性写出最值.
方法指导 结合二次函数的单调性和求最值的方法进行求解.
典例3
方法总结 1.二次函数在指定区间上的最值与二次函数图象的开口、对称轴有关,求解时要注意这两个因素.
2.图象直观,便于分析、理解;配方法说理更严谨,一般用于解答题.
练一练
整个上午(8:00~12:00)天气越来越暖,中午时分(12:00~13:00)一场暴风雨使天气骤然凉爽了许多,暴风雨过后,天气转暖,直到太阳落山(18:00)才又开始转凉. 画出这一天8:00~20:00的期间气温作为时间函数的一个可能的图象(示意图),并说出所画函数的单调区间.
解:函数的一个可能图象如图(1)所示:
单调增区间:[8,12),[13,18);
单调减区间:[12,13),[18,20].
图象的形状不是唯一的,只要能反映气温的变化情况即可
2. 设函数的定义域为[-6,11]. 如果 在区间[-6,2]上单调递减,在区间[2,11]上单调递增,画出 的一个大致的图象,从图象上可以发现 f(-2) 函数 f(x) 的一个__________.
解:
在区间[-6,11]上的大致图象如图所示.
最小值
3. 已知函数 ,求函数在区间[2,6]上的最大值和最小值.
解:
所以,函数 在区间[2,6]上单调递减.
C
B
B
求函数最值的方法
求函数最值的问题实质上就是求函数的值域问题,因此求函数值域的方法也可用来求函数最值。求函数最值的常用方法如下:(1)配方法:主要适用于二次函数或可化为二次函数的函数,要特别注意自变量的取值范围;(2)换元法:用换元法时一定要注意新元的取值范围;(3)数形结合法:对于图像较容易画出的函数的最值问题,可借助图像直观求出(4)利用数的单调性:要注意函数的单调性对函数最值的影响,特别是闭区间上函数的最值.
高中数学人教A版 (2019)必修 第一册3.2 函数的基本性质课文内容课件ppt: 这是一份高中数学人教A版 (2019)必修 第一册3.2 函数的基本性质课文内容课件ppt,共18页。PPT课件主要包含了导入新课,精彩课堂,应用举例,课堂练习,课堂总结等内容,欢迎下载使用。
高中数学人教A版 (2019)必修 第一册第三章 函数的概念与性质3.2 函数的基本性质课文课件ppt: 这是一份高中数学人教A版 (2019)必修 第一册第三章 函数的概念与性质3.2 函数的基本性质课文课件ppt,共22页。PPT课件主要包含了答案D等内容,欢迎下载使用。
高中数学人教A版 (2019)必修 第一册3.2 函数的基本性质教课课件ppt: 这是一份高中数学人教A版 (2019)必修 第一册3.2 函数的基本性质教课课件ppt,共44页。PPT课件主要包含了目标认知,fx≤M,fx0M,fx≥M,纵坐标,图3-2-5,图3-2-6,图3-2-7等内容,欢迎下载使用。













