北师大版八年级下册2 直角三角形完美版ppt课件

1.2  直角三角形

第2课时 直角三角形全等的判定

教学目标

1．会证明直角三角形全等的“HL”定理，并能利用“HL”定理解决实际问题．

2．进一步掌握推理证明的方法，提升演绎推理能力和思维能力．

教学重点难点

重点：直角三角形全等的判定方法（HL）．

难点：直角三角形全等的判定的应用．

教学过程

复习回顾

判定一般三角形全等的条件有哪几种？

SSS，SAS，ASA，AAS.

探究新知

一、合作探究

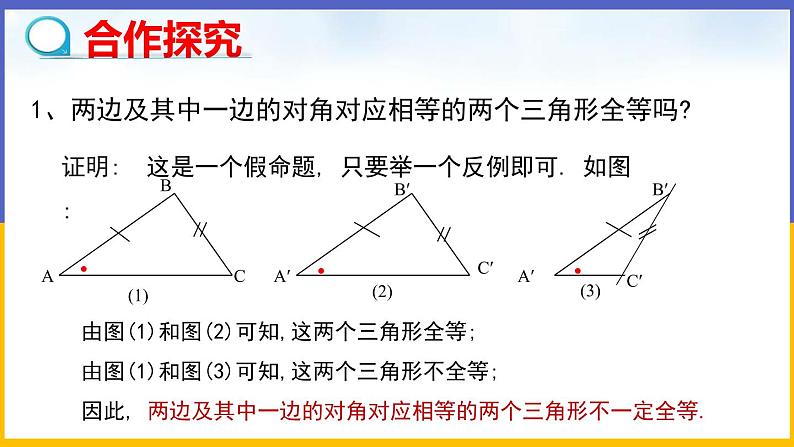
【问题】两边及其中一边的对角对应相等的两个三角形全等吗?

【探究】这是一个假命题, 只要举一个反例即可. 如图.

(1)                    (2)              (3) 

由图(1)和图(2)可知,这两个三角形全等;

由图(1)和图(3)可知,这两个三角形不全等.

【结论】两边及其中一边的对角对应相等的两个三角形不一定全等.

【互动】如果其中一组等边所对的角是直角, 那么这两个三角形全等吗？

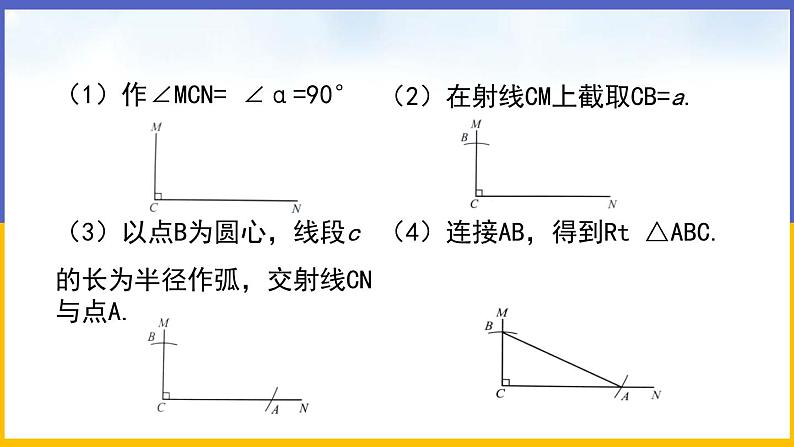
【操作】已知一条直角边和斜边，求作一个直角三角形.

已知：如图，线段a=4 cm，c=5 cm（a<c），直角 .

求作：Rt △ABC，使∠C= ∠ ，BC=a，AB=c.

（1）作∠MCN= ∠=90°.

（2）在射线CM上截取CB=a.

（3）以点B为圆心，线段c的长为半径作弧，交射线CN于点A.

（4）连接AB，得到Rt △ABC.

【互动】观察对比同桌作出的三角形是否全等？

把你们所作的三角形剪下来重叠在一起看是否重合？

【猜想】斜边和一条直角边分别相等的两个直角三角形全等.

【互动】如何证明我们猜想的正确性呢？

【探究】已知：如图, 在△ABC和△A′B′C′中,∠C=∠C′=90°, AC=A′C′,AB=A′B′.求证：△ABC≌△A′B′C′.

证明：在△ABC中，

∵∠C=90°，

∴BC2=AB2-AC2（勾股定理）.

同理，B′C′2=A′B′2-A′C′2 .

∵AB=A′B′，AC=A′C′，

∴BC=B′C′.

∴ △ABC≌△A′B′C′（SSS）.

【结论】定理：斜边和一条直角边对应相等的两个直角三角形全等.

简述为：“斜边、直角边”或“HL”.

几何语言：

在△ABC和△A′B′C′中, ∠C=∠C′=90，

∵ BC=B′C′,AB=A′B′，

∴ Rt△ABC≌Rt△A′B′C′.（HL）

二、新知应用

【例题】如图，有两个长度相等的滑梯，左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，两个滑梯的倾斜角 ∠B和∠F的大小有什么关系？

解：根据题意，可知∠BAC= ∠EDF=90°，AC=DF,BC=EF，

∴ Rt △BAC ≌Rt △EDF（HL）.

∴ ∠B= ∠DEF（全等三角形的对应角相等）.

∵ ∠DEF+ ∠F=90°（直角三角形的两锐角互余），

∴ ∠B+ ∠F=90°.

课堂小结

直角三角形全等的判定定理：斜边和一条直角边分别相等的两个直角三角形全等．这一定理可以简述为“斜边、直角边”或“HL”．

布置作业

教材习题1.6.

板书设计

2　直角三角形

第2课时 直角三角形全等的判定

直角三角形全等的判定定理：斜边和一条直角边分别相等的两个直角三角形全等．这一定理可以简述为“斜边、直角边”或“HL”．

例 如图，有两个长度相等的滑梯，左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，两个滑梯的倾斜角 ∠B和∠F的大小有什么关系？