初中数学北师大版八年级下册3 线段的垂直平分线精品精练

这是一份初中数学北师大版八年级下册3 线段的垂直平分线精品精练，共7页。试卷主要包含了3《线段的垂直平分线》等内容，欢迎下载使用。

一、选择题
1.如图，MN是线段AB的垂直平分线，C在MN外，且与A点在MN的同一侧，BC交MN于P点，则( )
A.BC＞PC＋AP B.BC＜PC＋AP C.BC＝PC＋AP D.BC≥PC＋AP
2.如图所示，在△ABC中，AB＋BC＝10，AC的垂直平分线分别交AB、AC于点D和点E，则△BCD的周长是( )
A.6 B.8 C.10 D.无法确定
3.如图，AC＝AD，BC＝BD，则有( )
A.AB垂直平分CD B.CD垂直平分AB
C.AB与CD互相垂直平分 D.CD平分∠ACB
4.如图，OP平分∠AOB，PA⊥OA，PB⊥OB，垂足分别为A、B，下列结论不一定成立的是( )
A.PA＝PB B.OA＝OB C.PO平分∠APB D.AB垂直平分OP
5.在Rt△ABC中，∠A＝40°，∠B＝90°，AC的垂直平分线MN分别与AB，AC交于点D，E，则∠BCD的度数为( )
A.10° B.15° C.40° D.50°
6.如图，在△ABC中，AB＝AC，D是BC的中点，AC的垂直平分线交AC，AD，AB于点E，O，F，则图中全等三角形的对数是( )
A.1对 B.2对 C.3对 D.4对
7.如图所示，在△ABC中，AD垂直平分BC，AC＝EC，点B，D，C，E在同一条直线上，则AB＋DB与DE之间的数量关系是( )
A.AB＋DB＞DE B.AB＋DB8.如图，已知AB＝AC，∠A＝36°，AC的垂直平分线MN交AB于D，AC于M.以下结论：
①△BCD是等腰三角形；
②射线CD是△ACB的角平分线；
③△BCD的周长C△BCD＝AB＋BC；
④△ADM≌△BCD.
正确的有( )
A.①② B.①③ C.②③ D.③④
二、填空题
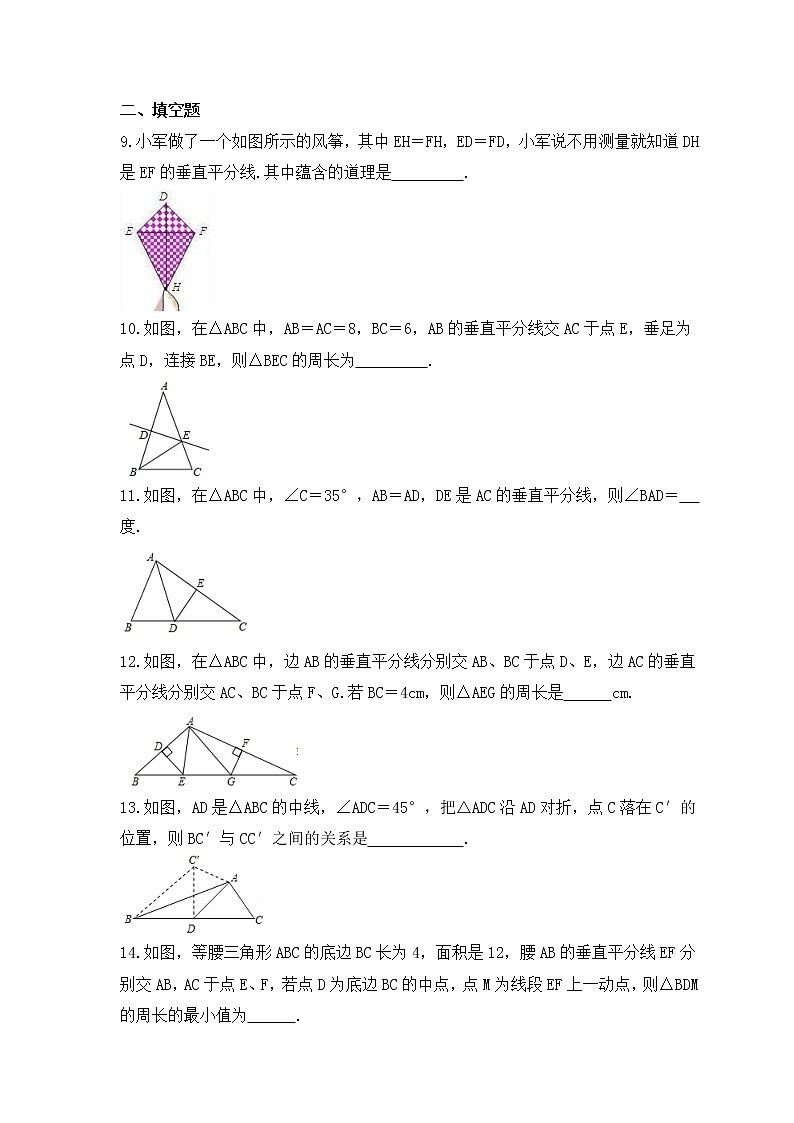
9.小军做了一个如图所示的风筝，其中EH＝FH，ED＝FD，小军说不用测量就知道DH是EF的垂直平分线.其中蕴含的道理是 .
10.如图，在△ABC中，AB＝AC＝8，BC＝6，AB的垂直平分线交AC于点E，垂足为点D，连接BE，则△BEC的周长为 .
11.如图，在△ABC中，∠C＝35°，AB＝AD，DE是AC的垂直平分线，则∠BAD＝ 度.
12.如图，在△ABC中，边AB的垂直平分线分别交AB、BC于点D、E，边AC的垂直平分线分别交AC、BC于点F、G.若BC＝4cm，则△AEG的周长是 cm.
13.如图，AD是△ABC的中线，∠ADC＝45°，把△ADC沿AD对折，点C落在C′的位置，则BC′与CC′之间的关系是 .
14.如图，等腰三角形ABC的底边BC长为4，面积是12，腰AB的垂直平分线EF分别交AB，AC于点E、F，若点D为底边BC的中点，点M为线段EF上一动点，则△BDM的周长的最小值为 .
三、解答题
15.如图，在Rt△ABC中，∠C＝90°，AB的垂直平分线DE交BC于点D，垂足为E，且∠CAD∶∠CAB＝1∶3，求∠B的度数.
16.在△ABC中，AB＞BC，AB＝AC，DE是AB的垂直平分线，垂足为D点，交AC于点E.
(1)若∠ABE＝38°，求∠EBC的度数；
(2)若△ABC的周长为36cm，一边为13cm，求△BCE的周长.
17.如图，已知P是线段CD的垂直平分线上一点，PC⊥OA，PD⊥OB，垂足为C、D.
求证:(1)OC＝OD;
(2)OP平分∠AOB.
18.已知：Rt△ABC中，∠ACB是直角，D是AB上一点，BD＝BC，过D作AB的垂线交AC于E.
求证：CD⊥BE.
19.如图.在△ABC中，BE是角平分线，AD⊥BE，垂足为D.
求证：∠2＝∠1＋∠C.
参考答案
1.C.
2.C
3.A
4.D
5.A
6.D.
7.C
8.B
9.答案为：与线段两个端点距离相等的点在这条线段的垂直平分线线上.
10.答案为：14.
11.答案为：40.
12.答案为：4.
13.答案为：垂直且相等
14.答案为：8.
15.解：设∠CAD＝x°，
则∠CAB＝3x°，∠BAD＝2x°.
∵DE是AB的垂直平分线，
∴DA＝DB，
∴∠B＝∠BAD＝2x°.
∵∠C＝90°，
∴∠CAB＋∠B＝90°，
即3x＋2x＝90，解得x＝18，
∴∠B＝2×18°＝36°.
16.解：∵DE是AB的垂直平分线，
∴AE＝BE，
∴∠A＝∠ABE＝38°
∵AB＝AC，
∴∠ABC＝∠C＝71°
∴∠EBC＝∠ABC-∠ABE＝71°-38°＝33°
由△ABC的周长为36cm
AB＞BC，AB＝AC可知AB＝AC＝13cm BC＝10cm
△BCE的周长＝BE＋CE＋BC＝AC＋BC＝13＋10＝23(cm)
17.证明：(1)∵P在CD的垂直平分线上，
∴PC＝PD.
又∵OP＝OP，
∴Rt△OPC≌Rt△OPD(HL).
∴OC＝OD.
(2)由(1)Rt△OPC≌△OPD知∠AOP＝∠BOP.
18.证明：∵DE⊥AB
∴∠BDE＝90°，
∵∠ACB＝90°
∴在Rt△DEB中与Rt△CEB中
BD＝BC，BE＝BE
∴Rt△DEB≌Rt△CEB(HL)
∴DE＝EC
又∵BD＝BC
∴E、B在CD的垂直平分线上
即BE⊥CD.
19.证明：如图，延长AD交BC于点F，
∵BE是角平分线，AD⊥BE，
∴△ABF是等腰三角形，且∠2＝∠AFB，
又∵∠AFB＝∠1＋∠C，
∴∠2＝∠1＋∠C.