

高教版(2021)基础模块上册2.4 含绝对值的不等式授课ppt课件
展开关于绝对值还有什么性质呢?
表示数轴上坐标为a的点A到原点O的距离.
证明:10 .当ab≥0时,
20. 当ab<0时,
综合10,20知定理成立.
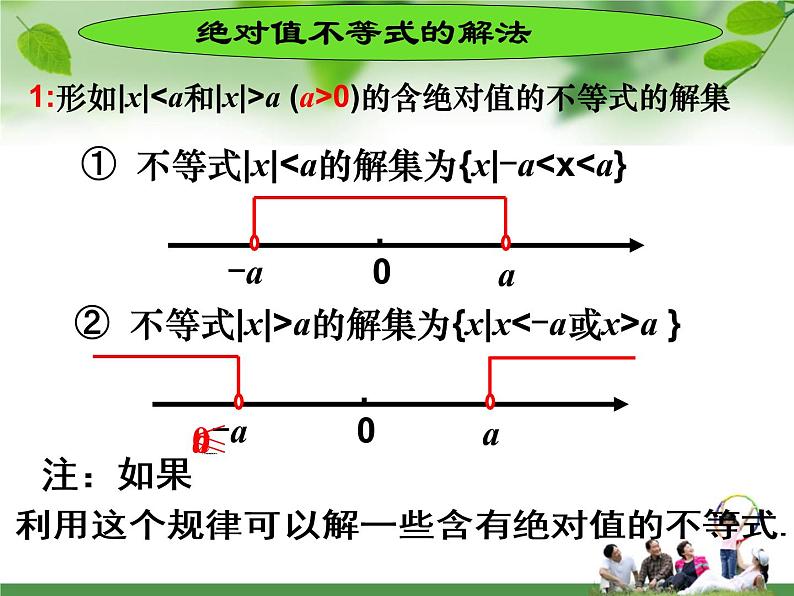
1:形如|x|
① 不等式|x|
解:对绝对值里面的代数式符号讨论:
(Ⅰ) 或 (Ⅱ)
解(Ⅰ)得:6/5≤x<2
解(Ⅱ) 得:0
解不等式 | 5x-6 | < 6 – x
(Ⅰ)当5x-6≥0,即x≥6/5时,不等式化为
5x-6<6-x,解得x<2,
(Ⅱ)当5x-6<0,即x<6/5时,不等式化为
-(5x-6)<6-x,解得x>0 所以0
2.型如|ax+b|≤c,|ax+b|≥c(c∈R)不等式解法
3.型如|ax+b|+|cx+d|≥k(k∈R)不等式解法
例 解不等式|x-1|+|x+2|≥5
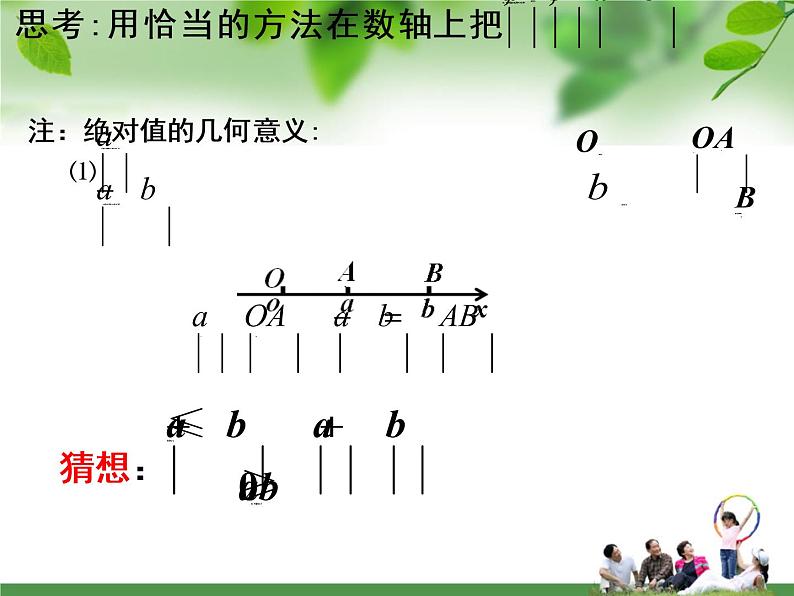
方法一:利用绝对值的几何意义,体现了数型结合的思想.
解:|x-1|+|x+2|=5的解为x=-3或x=2
高教版(2021)第2章 不等式2.4 含绝对值的不等式说课免费课件ppt: 这是一份高教版(2021)第2章 不等式2.4 含绝对值的不等式说课免费课件ppt,共15页。PPT课件主要包含了情境导入,探索新知,例题辨析,巩固练习,归纳总结,布置作业等内容,欢迎下载使用。
高教版(中职)基础模块上册(2021)2.4 含绝对值的不等式备课课件ppt: 这是一份高教版(中职)基础模块上册(2021)2.4 含绝对值的不等式备课课件ppt,文件包含25不等式应用举例课件pptx、25不等式应用举例教案pdf、25不等式应用举例docx等3份课件配套教学资源,其中PPT共17页, 欢迎下载使用。
高教版(中职)基础模块上册(2021)2.4 含绝对值的不等式教学演示ppt课件: 这是一份高教版(中职)基础模块上册(2021)2.4 含绝对值的不等式教学演示ppt课件,文件包含24含绝对值的不等式课件pptx、24含绝对值的不等式教案pdf等2份课件配套教学资源,其中PPT共20页, 欢迎下载使用。












