鲁教版 (五四制)八年级下册4 探索三角形相似的条件学案及答案
展开
这是一份鲁教版 (五四制)八年级下册4 探索三角形相似的条件学案及答案,共3页。
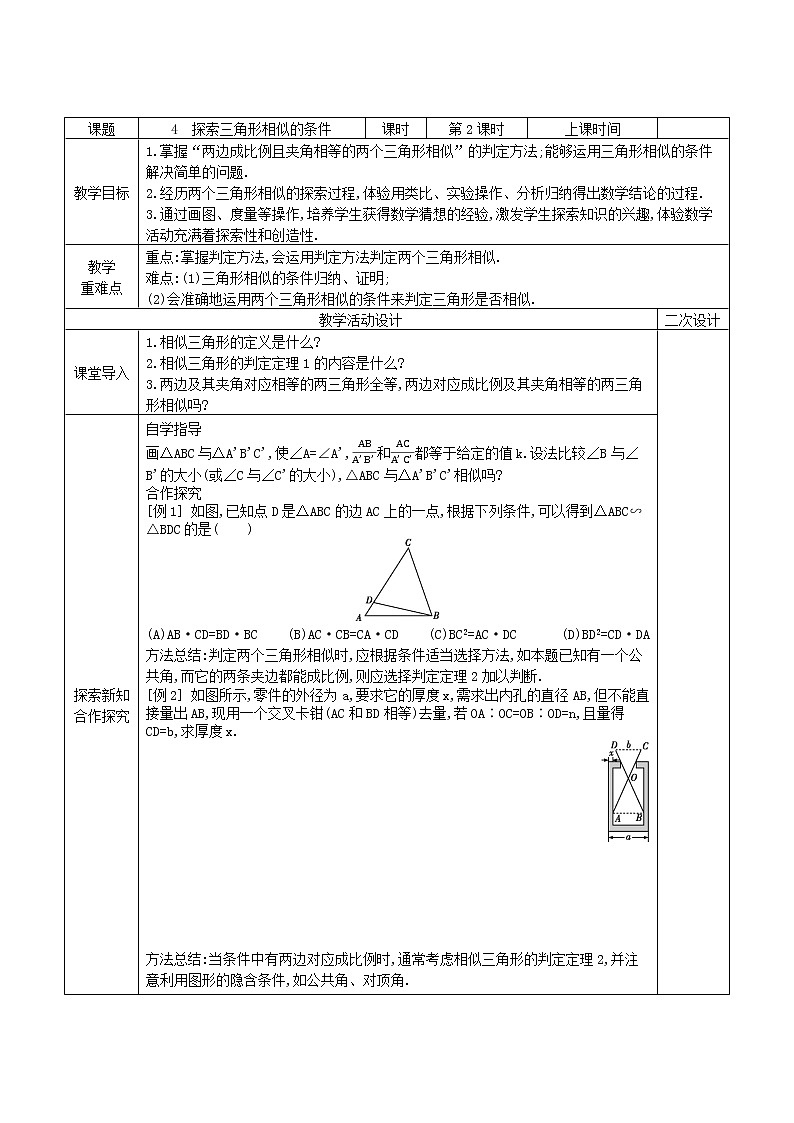
课题4 探索三角形相似的条件课时第2课时上课时间 教学目标1.掌握“两边成比例且夹角相等的两个三角形相似”的判定方法;能够运用三角形相似的条件解决简单的问题.2.经历两个三角形相似的探索过程,体验用类比、实验操作、分析归纳得出数学结论的过程.3.通过画图、度量等操作,培养学生获得数学猜想的经验,激发学生探索知识的兴趣,体验数学活动充满着探索性和创造性.教学重难点重点:掌握判定方法,会运用判定方法判定两个三角形相似.难点:(1)三角形相似的条件归纳、证明;(2)会准确地运用两个三角形相似的条件来判定三角形是否相似.教学活动设计二次设计课堂导入1.相似三角形的定义是什么?2.相似三角形的判定定理1的内容是什么?3.两边及其夹角对应相等的两三角形全等,两边对应成比例及其夹角相等的两三角形相似吗? 探索新知合作探究自学指导画△ABC与△A'B'C',使∠A=∠A',和都等于给定的值k.设法比较∠B与∠B'的大小(或∠C与∠C'的大小),△ABC与△A'B'C'相似吗?合作探究[例1] 如图,已知点D是△ABC的边AC上的一点,根据下列条件,可以得到△ABC∽△BDC的是( )(A)AB·CD=BD·BC (B)AC·CB=CA·CD (C)BC2=AC·DC (D)BD2=CD·DA方法总结:判定两个三角形相似时,应根据条件适当选择方法,如本题已知有一个公共角,而它的两条夹边都能成比例,则应选择判定定理2加以判断.[例2] 如图所示,零件的外径为a,要求它的厚度x,需求出内孔的直径AB,但不能直接量出AB,现用一个交叉卡钳(AC和BD相等)去量,若OA∶OC=OB∶OD=n,且量得CD=b,求厚度x. 方法总结:当条件中有两边对应成比例时,通常考虑相似三角形的判定定理2,并注意利用图形的隐含条件,如公共角、对顶角. 续表探索新知合作探究[例3] 如图,在△ABC中,AB=8 cm,BC=16 cm,点P从点A开始沿AB向点B以1 cm/s的速度移动,点Q从点B开始沿BC向点C以2 cm/s的速度移动.如果点P,Q同时出发,经过多长时间后△PBQ与△ABC相似? 分析:要证明△PBQ与△ABC相似,很显然∠B为公共角,因此可运用两边对应成比例且夹角相等来得到相似,根据对应边成比例列方程求解,同时要注意分类讨论.教师提醒:在点运动的情况下寻找相似的条件,随着点的位置的变化,△PBQ的形状也会发生变化,因此既要考虑△PBQ∽△ABC的情况,还要考虑△PBQ∽△CBA的情况.教师指导1.易错点:两边对应成比例并且必须是夹角对应相等两三角形才一定相似.2.归纳小结:两边对应成比例且夹角相等的两个三角形相似.3.方法规律:灵活选用判定定理的关键所在.(1)已知等积式或比例式,关键是来证明成比例两边的夹角相等,选用判定定理2;(2)如果已知条件只有角相等,就选用判定定理1. 当堂训练1.下列条件能判断△ABC和△A'B'C'相似的是( )(A)= (B)=且∠A=∠C'(C)=且∠B=∠A' (D)=且∠B=∠B'2.如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与左图中△ABC相似的是( )3.已知:如图,在△ABC中,CE⊥AB,BF⊥AC.求证:△AEF∽△ACB. 板书设计利用两边及其夹角判定两三角形相似相似三角形的判定定理2:两边成比例且夹角相等的两个三角形相似教学反思经历两个三角形相似的探索过程,体验分析归纳得出数学结论的过程,培养学生的观察、发现、比较、归纳能力,进一步发展学生的探究、交流能力.感受两个三角形相似的判定定理2与全等三角形判定定理(SAS)的区别与联系,体验事物间特殊与一般的关系.
相关学案
这是一份初中数学鲁教版 (五四制)八年级下册1 菱形的性质与判定导学案,共2页。
这是一份鲁教版 (五四制)八年级下册2 矩形的性质与判定学案及答案,共3页。
这是一份初中数学鲁教版 (五四制)八年级下册9 利用位似放缩图形导学案,共3页。










