
苏科版七年级上册6.2 角同步达标检测题
展开6.2 角
1.(2022·江苏连云港·七年级期末)如图,某测绘装置上一枚指针原来指向南偏西,把这枚指针按逆时针方向旋周,则指针的指向是( )
A.南偏东 B.南偏北 C.南偏东 D.东南方向
2.(2022·江苏淮安·七年级期末)如图, 为北偏东方向,,则的方向为( )
A.南偏东 B.南偏东 C.南偏西 D.北偏东
3.(2022·江苏徐州·七年级期末)上午10:00,钟面上时针与分针所成角的度数是( )
A.30° B.45° C.60° D.75°
4.(2022·江苏江苏·七年级期末)学校早上8:20上第一节课,40分钟后下课,这节课中分针转动的角度为( )
A.180° B.240° C.270° D.200°
5.(2022·江苏无锡·七年级期末)将一副三角板按如图所示位置摆放,其中与一定相等的是( )
A. B.
C. D.
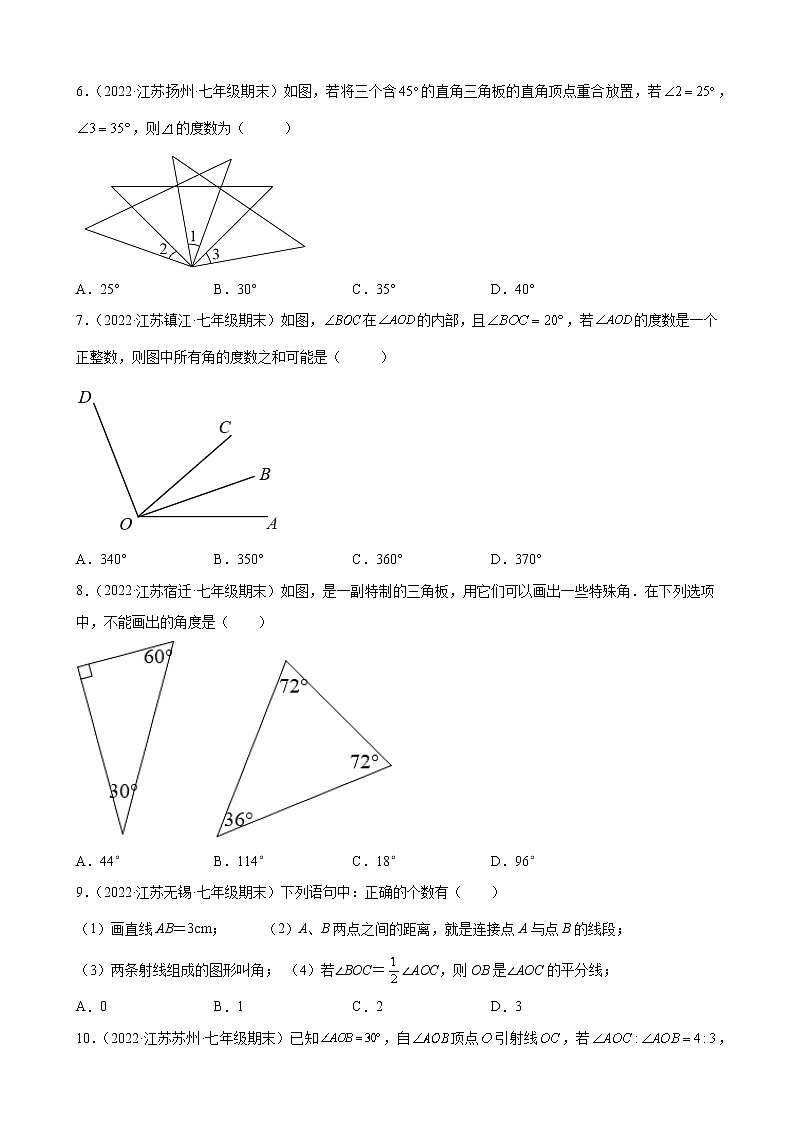
6.(2022·江苏扬州·七年级期末)如图,若将三个含的直角三角板的直角顶点重合放置,若,,则的度数为( )
A.25° B.30° C.35° D.40°
7.(2022·江苏镇江·七年级期末)如图,在的内部,且,若的度数是一个正整数,则图中所有角的度数之和可能是( )
A.340° B.350° C.360° D.370°
8.(2022·江苏宿迁·七年级期末)如图,是一副特制的三角板,用它们可以画出一些特殊角.在下列选项中,不能画出的角度是( )
A.44° B.114° C.18° D.96°
9.(2022·江苏无锡·七年级期末)下列语句中:正确的个数有( )
(1)画直线AB=3cm; (2)A、B两点之间的距离,就是连接点A与点B的线段;
(3)两条射线组成的图形叫角; (4)若∠BOC=∠AOC,则OB是∠AOC的平分线;
A.0 B.1 C.2 D.3
10.(2022·江苏苏州·七年级期末)已知,自顶点引射线,若,那么的度数是( )
A.10° B.40° C.70° D.10°或70°
11.(2022·江苏淮安·七年级期末)如图,一副三角板(直角顶点重合)摆放在桌面上,若∠AOD=150°,则∠BOC等于_________度.
12.(2022·江苏南通·七年级期末)如图,OA的方向是北偏东15度,OB的方向是西偏北50度,若∠AOC=∠AOB,则OC的方向是_____.
13.(2022·江苏盐城·七年级期末)如图,在∠AOB的内部以O为端点引出1条射线,那么图中共有3个角;如果引出2条射线,共有6个角;如果引出n条射线,共有______个角.
14.(2022·江苏南通·七年级期末)如图,是表示北偏西方向的一条射线,是表示西南方向的一条射线,则______.
15.(2022·江苏盐城·七年级期末)已知射线OA与射线OB垂直,射线OA表示的方向是北偏西25°方向,则射线OB表示的方向为南偏西________方向.
16.(2022·江苏扬州·七年级期末)______°.
17.(2022·江苏无锡·七年级期末)已知,,则________(填>、=或<).
18.(2022·江苏·射阳县第六中学七年级期末)如图,将一个三角板60°角的顶点与另一个三角板的直角顶点重合,∠1=27°,∠2=_____.
19.(2022·江苏苏州·七年级期末)已知∠AOB=50°,∠BOC=30°,则∠AOC=_____.
20.(2022·江苏无锡·七年级期末)如图,将一副三角板的直角顶点O叠放在一起,∠BOC=∠AOD,则∠BOD=_____°.
21.(2022·江苏南京·七年级期末)如图,在的内部有3条射线、、,若,,,则__________.
22.(2022·江苏扬州·七年级期末)如图,O为直线AB上一点,过点O作射线OC,使∠BOC=60°,将一个直角三角尺POQ如图摆放,直角顶点在点O处,一条直角边OP在射线OA上.将三角尺绕点O以每秒10°的速度按逆时针方向旋转,记旋转后的三角尺为,在旋转一周的过程中,第t秒时,所在直线恰好平分∠BOC,则t的值为___.
23.(2022·江苏无锡·七年级期末)一块手表上午6点45分,此时时针分针所夹锐角的大小为__________度.
24.(2022·江苏南京·七年级期末)如图,射线OA所表示的方向是______.
25.(2022·江苏·南京市第二十九中学七年级期末)如图,将一副三角板的直角顶点重合,摆放在桌面上,当∠AOC=__________时,AB所在直线与CD所在直线互相垂直.
26.(2022·江苏苏州·七年级期末)如图,已知∠AOB=2∠BOC,OD平分∠AOC,且∠BOD=20°,则∠AOC的度数为______°.
27.(2022·江苏常州·七年级期末)OC、OD是∠AOB内部任意两条射线线,OM平分∠AOC,ON平∠BOD,若∠MON=m°,∠COD=n°,则∠AOB=_____________°(用含m、n的代数式表示).
28.(2022·江苏南京·七年级期末)一副三角板AOB与COD如图摆放,且∠A=∠C=90°,∠AOB=60°,∠COD=45°,ON平分∠COB,OM平分∠AOD.当三角板COD绕O点顺时针旋转(从图1到图2).设图1、图2中的∠NOM的度数分别为α,β,=______度.
29.(2022·江苏南京·七年级期末)如图,、是内的两条射线,平分,平分,若,,则_______°(用含m、n的代数式表示).
30.(2022·江苏扬州·七年级期末)如图,在三角形中,,点为边上一个动点,连接,把三角形沿着折叠,当时,则______.
31.(2022·江苏苏州·七年级期末)如图,直线、相交于点,将一个直角三角尺的直角顶点放置在点处,且平分.
(1)若,求的度数;
(2)试说明平分.
32.(2022·江苏南通·七年级期末)新定义:若∠α的度数是∠β的度数的n倍,则∠α叫做∠β的n倍角.
(1)若∠M=10°21′,请直接写出∠M的3倍角的度数;
(2)如图1,若∠AOB=∠BOC=∠COD,请直接写出图中∠AOB的所有2倍角;
(3)如图2,若∠AOC是∠AOB的3倍角,∠COD是∠AOB的4倍角,且∠BOD=90°,求∠BOC的度数.
33.(2022·江苏南通·七年级期末)点O在直线AD上,在直线AD的同侧作射线OB,OC.
(1)如图1,若,,求的度数;
(2)如图2,若OM平分,ON平分,,求的度数.
34.(2022·江苏南京·七年级期末)如图1,线段AB=20cm.
(1)点P沿线段AB自A点向B点以2cm/s的速度运动,同时点Q沿线段BA自B点向A点以3cm/s的速度运动,几秒后,P,Q两点相遇?
(2)如图2,AO=PO=2cm,∠POQ=60°,现点P绕着点O以30°/s的速度顺时针旋转一周后停止,同时点Q沿直线BA自B点向A点运动,若点P,Q两点也能相遇,求点Q运动的速度.
35.(2022·江苏无锡·七年级期末)已知O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)如图①,若∠AOC=30°,求∠DOE的度数.
(2)在图①中,若∠AOC=α,求∠DOE的度数(用含α的代数式表示).
(3)将图①中的∠DOC绕顶点O顺时针旋转至图②的位置,且保持射线OC在直线AB上方,在整个旋转过程中,当∠AOC的度数是多少时,∠COE=2∠DOB.
36.(2022·江苏南京·七年级期末)如图,已知∠AOB=40°,∠BOC=3∠AOB,OD平分∠AOC,求∠COD的度数.
解:因为∠BOC=3∠AOB,∠AOB=40°
所以∠BOC=_____°,
所以∠AOC=_____+_____=____°+_____°=______°,
因为OD平分∠AOC,
所以∠COD=_____=_______°.
37.(2022·江苏南京·七年级期末)如图,已知直线 AB 和 CD 相交于点O,∠COE=90°,OF 平分∠AOE,∠COF=37°.
(1)求∠EOB的度数.
(2)若射线OF、OD分别绕着点O按顺时针方向转动,两射线同时出发,射线OF每分钟转动6°,射线OD每分钟转动0.5°,多少分钟后,射线OF与射线OD第一次重合.
(3)在(2)的条件下,假设转动时间不超过60分钟,若∠FOD=33°,则两射线同时出发 分钟.
38.(2022·江苏无锡·七年级期末)如图,已知直线AB、CD相交于点O,OE⊥AB,点O为垂足,OF平分∠AOC.
(1)若∠COE=54°,求∠DOF的度数;
(2)若∠COE:∠EOF=2:1,求∠DOF的度数.
39.(2022·江苏·南京市第二十九中学七年级期末)如图1,点A、O、B依次在直线MN上,如图2,现将射线OA绕点O沿顺时针方向以每秒4°的速度旋转,同时射线OB绕点O沿逆时针方向以每秒6°的速度旋转,当其中一条射线回到起始位置时,运动停止,直线MN保持不动,设旋转时间为ts.
(1)当t=3时,∠AOB= ;
(2)在运动过程中,当射线OB与射线OA垂直时,求t的值;
(3)在旋转过程中,是否存在这样的t,使得射线OB、射线OA和射线OM,其中一条射线把另外两条射线的夹角(小于180°)分成2:3的两部分?如果存在,直接写出答案;如果不存在,请说明理由.
(2022·江苏扬州·七年级期末)如图,已知同一平面内,∠AOB=90°,∠AOC=60°.
40.填空:∠COB= ;
41.如OD平分∠BOC,OE平分∠AOC,直接写出∠DOE的度数为 ;
42.试问在(2)的条件下,如果将题目中∠AOC=60°改成∠AOC=2α(α<45°),其他条件不变,你能求出∠DOE的度数吗?若能,请你写出求解过程;若不能,请说明理由.
43.(2022·江苏无锡·七年级期末)类比角平分线的概念,如果一条射线把一个角分成1:2两部分,则称这条射线为这个角的一条三等分线,
(1)如图,已知,是的一条三等分线,.且,求的度数;
(2)如图,,是的一条三等分线(),是的角平分线,是的角平分线.若以每秒5的速度绕点O逆时针旋转一周,旋转时间为t秒,当t为何值时,射线恰好是的一条三等分线.
44.(2022·江苏·射阳县第六中学七年级期末)如图1:已知OB⊥OD,OA⊥OC,∠COD=40°,若射线OA绕O点以每秒30°的速度顺时针旋转,射线OC绕O点每秒10°的速度逆时针旋转,两条射线同时旋转,当一条射线与射线OD重合时,停止运动.
(1)开始旋转前,∠AOB= .
(2)若射线OB也绕O点以每秒20°的速度顺时针旋转,三条射线同时旋转,当一条射线与射线OD重合时,停止运动.当三条射线中其中一条射线是另外两条射线夹角的角平分线时,求旋转的时间.
(3)【实际应用】从今天上午6时整开始到上午7时整结束的运动过程中,经过多少分钟时针与分针所形成的钝角等于120°(直接写出所有可能结果).
45.(2022·江苏盐城·七年级期末)【阅读理解】射线是内部的一条射线,若,则我们称射线是射线的“友好线”,例如,如图1,,,则,称射线是射线的友好线:同时,由于,称射线是射线的友好线.
(1)如图2,,射线是射线的友好线,则________;
(2)如图3,,射线与射线重合,并绕点以每秒的速度逆时针旋转,射线与射线重合,并绕点以每秒3゜的速度顺时针旋转,当射线与射线重合时,运动停止;
①是否存在某个时刻(秒),使得的度数是,若存在,求出的值,若不存在,请说明理由;
②当为多少秒时,射线、、中恰好有一条射线是另一条射线的友好线.(直接写出答案)
46.(2022·江苏淮安·七年级期末)如图 1,射线OC 在ÐAOB 的内部,图中共有 3 个角:ÐAOB 、ÐAOC 和ÐBOC ,若其中有一个角的度数是另一个角度数的两倍,则称射线OC 是ÐAOB 的奇妙线.
(1)一个角的角平分线 这个角的奇妙线.(填是或不是)
(2)如图 2,若ÐMPN = 60° ,射线 PQ 绕点 P 从 PN 位置开始,以每秒10° 的速度逆时针旋转, 当ÐQPN 首次等于180° 时停止旋转,设旋转的时间为t(s) .
①当t 为何值时,射线 PM 是ÐQPN 的奇妙线?
②若射线 PM 同时绕点 P 以每秒6° 的速度逆时针旋转,并与 PQ 同时停止旋转.请求出当射线 PQ 是ÐMPN 的奇妙线时t 的值.
47.(2022·江苏淮安·七年级期末)
【阅读理解】
射线OC是∠AOB内部的一条射线,若∠AOC=∠BOC,则称射线OC是射线OA在∠AOB内的一条“友好线”.如图1,若∠AOB=75°,∠AOC=25°,则∠AOC=∠BOC,所以射线OC是射线OA在∠AOB内的一条“友好线”.
【解决问题】
(1)在图1中,若作∠BOC的平分线OD,则射线OD (填“是”或“不是”)射线OB在∠AOB内的一条“友好线”;
(2)如图2,∠AOB的度数为n,射线OM是射线OB在∠AOB内的一条“友好线”,ON平分∠AOB,则∠MON的度数为 (用含n的代数式表示);
(3)如图3,射线OB先从与射线OA重合的位置出发,绕点O以每秒1°的速度逆时针旋转;10秒后射线OC也从与射线OA重合的位置出发,绕点O以每秒5°的速度逆时针旋转,当射线OC与射线OA的延长线重合时,运动停止.问:当射线OC运动时间为多少秒时,射线OA,OB,OC中恰好有一条射线是余下两条射线中某条射线在余下两条射线所组成的角内的一条“友好线”?
48.(2022·江苏南京·七年级期末)如图,两条直线AB,CD相交于点O,且∠AOC=∠AOD,射线OM从OB开始绕O点逆时针方向旋转,速度为15°/s,射线ON同时从OD开始绕O点顺时针方向旋转,速度为12°/s,运动时间为t秒(0<t<12,本题出现的角均小于平角)
(1)图中一定有 个直角;当t=2时,∠MON的度数为 ,∠BON的度数为 ;
(2)若OE平分∠COM,OF平分∠NOD,当∠EOF为直角时,请求出t的值;
(3)当射线OM在∠COB内部,且是定值时,求t的取值范围,并求出这个定值.
参考答案:
1.C
【解析】根据方位角的概念,画图正确表示出方位角,即可求解.
解:如图,
指针按逆时针方向旋转周,即转90度,
指针的指向是南偏东40°方向.
故选:C.
本题考查了方位角.解答此类题需要从运动的角度,正确画出方位角是解题的关键.
2.A
【解析】利用已知得出∠1的度数,进而得出OB的方向角.
解:如图所示:
∵OA是北偏东方向的一条射线,∠AOB=90°,
∴∠1=90°-44°=46°,
∴OB的方向角是南偏东46°.
故选:A.
此题主要考查了方向角,正确利用互余的性质得出∠1度数是解题关键.
3.C
【解析】钟面一周为360°,共分12大格,每格为360÷12=30°,10时整,时针在10,分针在12,相差2格,组成的角的度数就是30°×2=60°,
10时整,时针与分针组成的角的度数是30°×2=60°.
故选:C.
本题要在了解钟面结构的基础上进行解答.
4.B
【解析】根据分针一小时(60分钟)转360度进行求解即可.
解:∵分针一小时(60分钟)转360度,
∴一节课40分钟分针转动的角度,
故选B.
本题主要考查了钟面角,解题的关键在于能够熟练掌握分针一小时转360度.
5.A
【解析】根据图形中两个角的位置关系确定度数关系,据此判断.
A、=,故符合题意;
B、,故与不相等,故不符合题意;
C、+=,故不符合题意;
D、+=,故不符合题意;
故选:A.
此题考查三角板中角度关系计算,熟记三角板中各角度数,根据图形确定两个角的位置关系进行计算度数关系是解题的关键.
6.B
【解析】根据题意可知,代入数值求解即可.
如图,
三个含的直角三角板的直角顶点重合放置,,,
故选B
本题考查了几何图形中角度的计算,三角板中角度的计算,得出是解题的关键.
7.B
【解析】根据角的运算和题意可知,所有角的度数之和是∠AOB+∠BOC+∠COD+∠AOC+∠BOD+
∠AOD,然后根据,的度数是一个正整数,可以解答本题.
解:由题意可得,图中所有角的度数之和是
∠AOB+∠BOC+∠COD+∠AOC+∠BOD+∠AOD=3∠AOD+∠BOC
∵,的度数是一个正整数,
∴A、当3∠AOD+∠BOC=340°时,则= ,不符合题意;
B、当3∠AOD+∠BOC=3×110°+20°=350°时,则=110°,符合题意;
C、当3∠AOD+∠BOC=360°时,则=,不符合题意;
D、当3∠AOD+∠BOC=370°时,则=,不符合题意.
故选:B.
本题考查角度的运算,解题的关键是明确题意,找出所求问题需要的条件.
8.A
【解析】根据角度的和差计算即可判断.
解:A、44°的角不能由30°、36°、60°、72°角的和或差关系得到,故不能画出44°角;
B、114°=72°+72°-30°,故可以画出114°角;
C、18°=72°+36°-30°-60°,故可以画出18°角;
D、96°=36°+60°,故可以画出96°角;
故选:A.
此题考查了角度的和差计算,正确进行角度的和差计算是解题的关键.
9.A
【解析】根据直线,线段,角和角平分线的定义进行逐一判断即可得到答案.
解:直线是没有端点,两端可以无限延伸,直线没有长度,故(1)说法错误;
A、B两点之间的距离,就是连接点A与点B的线段的长度,故(2)说法错误;
两条有公共端点的射线组成的图形是角,故(3)说法错误;
若∠BOC=∠AOC,且B在∠AOC内则OB是∠AOC的平分线,故(4)说法错误;
故选A.
本题主要考查了直线,线段,角和角平分线的定义,解题的关键在于能够熟练掌握相关定义.
10.D
【解析】分为两种情况:①OC和OB在OA的两侧时,②OC和OB在OA的同侧时,分别进行求解即可.
∵∠AOB=30°,∠AOC:∠AOB=4:3,
∴∠AOC=40°,
分为两种情况:
当OC和OB在OA的两侧时,如图1
∠BOC=∠AOB+∠AOC=30°+40°=70°
②OC和OB在OA的同侧时,如图2
∠BOC=∠AOC-∠AOB=40°-30°=10°
故选:D.
考查了角的计算,解题关键是分两种情况:OC、OB在OA的两侧时和OC、OB在OA的同侧时.
11.30
【解析】由图象可知,两个三角板直角组成∠AOD,其中∠COB为重合部分,故有∠AOD=∠AOB+∠COD-∠COB,易求得∠COB=30°.
已知三角板的角∠AOB=∠COD=90°
有∠AOD=∠AOB+∠COD-∠COB
即150°=90°+90°-∠COB
解得∠COB=30°.
故答案为:30.
本题考查了三角板中的角度问题,结合三角板的等腰直角三角形和30°、60°直角三角形的性质计算即可.
12.北偏东70°
【解析】根据角的和差关系可求出∠AOB的度数,根据∠AOC=∠AOB可得OC的方向角,根据方向角的概念即可得答案.
∵OA的方向北偏东方向15°,OB的方向西偏北方向50°,
∴∠AOB=90°-50°+15°=55°,
∵∠AOC=∠AOB,
∴∠AOC=55°,
∵15°+55°=70°,
∴OC的方向为北偏东70°.
故答案为:北偏东70°.
本题考查方向角,方向角是表示方向的角,以正北或正南为基准,来描述物体所处的方向;根据题意求出各角的度数是解答此题的关键.
13.
【解析】首先分析在∠AOB的内部以O端点引1条射线,有1+2个角,引2条线段,有1+2+3个角,···进而得出引n条线段,有角的个数,得出答案即可.
在∠AOB的内部以O端点引1条射线,有1+2=3(个)角,
引2条线段,有1+2+3=6(个)角,
···
引n条线段,有(个)角,
故答案为:.
本题主要考查了数角的个数,掌握数字变化规律式解题的关键.
14.
【解析】根据方向角的定义求解即可.
解:∵OA是表示北偏西56°方向的一条射线,
∴∠1=56°,
∴∠2=34°.
∵OB是表示西南方向的一条射线,
∴∠3=∠4=45°,
∴∠AOB=34°+45°=79°.
故答案为:79°.
本题考查了方向角及其计算.解题的关键是掌握方向角的定义.在观测物体时,地球南北方向与观测者观测物体视线的夹角叫做方向角.
15.
【解析】如图(见解析),先根据射线的方位角可得,再根据角的和差即可得.
解:如图,由题意得:,,
则,
即射线表示的方向为南偏西方向,
故答案为:.
本题考查了方位角、角的和差、垂直,掌握理解方位角是解题关键.
16.42.6
【解析】根据角度进制的转化求解即可,.
解:
42.6
故答案为:42.6
本题考查了角度进制的转化,掌握角度进制是解题的关键.
17.<
【解析】先把化为再比较大小即可.
解: ,
故答案为:
本题考查的是角度的换算,角度的大小比较,掌握“大化小用乘法,小化大用除法”是解本题的关键.
18.57°##57度
【解析】先利用∠1求出∠EAC的度数,再利用90°减去∠EAC即可解答.
解:∵∠BAC=60°,∠1=27°,
∴∠EAC=∠BAC-∠1=60°-27°=33°,
∵∠EAD=90°,
∴∠2=∠EAD-∠EAC=90°-33°=57°,
故答案为:57°.
本题考查角的和差,题目较容易,根据已知求出∠EAC便可求出答案.
19.20°或80°
解:当OC在∠AOB内部,如图1,
因为∠AOB=50°,∠BOC=30°,
所以∠AOC=50-30°=20°;
当OC在∠AOB外部,如图2,
因为∠AOB=50°,∠BOC=30°,
所以∠AOC=50°+30°=80°;
综上可知,∠AOC为20°或80°.
故答案为:20°或80°.
20.70
【解析】根据已知求出∠AOD+∠BOC=180°,再根据∠BOC=∠AOD求出∠AOD,即可求出答案.
解:∵∠AOB=∠COD=90°,
∴∠AOD+∠BOC
=∠AOB+∠DOB+∠BOC
=∠AOB+∠COD
=90°+90°
=180°,
∵∠BOC=∠AOD,
∴∠AOD+∠AOD=180°,
∴∠AOD=160°,
∴∠BOD=∠AOD﹣∠AOB=160°﹣90°=70°,
故答案为:70.
本题考查了余角和补角的应用,能求出∠AOD+∠BOC=180°是解此题的关键.
21.13
【解析】先用含∠BOE的代数式表示出∠AOB,进而表示出∠BOD,然后根据∠DOE=∠BOD-∠BOE即可得到结论.
解:∵∠BOE=∠BOC,
∴∠BOC=4∠BOE,
∴∠AOB=∠AOC+∠BOC=52°+4∠BOE,
∴∠BOD=∠AOB=+∠BOE,
∴∠DOE=∠BOD-∠BOE=,
故答案为:13.
本题考查了角的和差倍分计算,正确的识别图形是解题的关键.
22.12或30
【解析】根据角平分线定义列出方程即可求解.
解:∵∠BOC=60°且OQ所在直线恰好平分∠BOC,
∴∠BOQ=∠BOC=30°或∠BOQ=180°+30°=210°,
∴10t=30+90或10t=90+210,
解得t=12或30.
故答案为:12或30.
本题考查了一元一次方程的应用,角平分线定义,列出正确的方程是解本题的关键.
23.67.5
【解析】6点45分时,分针指向9,时针在指向6与7之间,则时针45分钟转过的角度即为6时45分时,时钟的时针与分针的夹角度数,根据时针每分钟转0.5°,计算2×30°+30°-0.5°×45即可.
解:∵6点45分时,分针指向9,时针在指向6与7之间,
∴时针45分钟转过的角度即为6时45分时,时钟的时针与分针的夹角度数,即2×30°+30°-0.5°×45=67.5°.
故答案为:67.5.
本题考查了钟面角:钟面被分成12大格,每格30°;分针每分钟转6°,时针每分钟转0.5°.
24.北偏东54°
【解析】根据互余先计算出OA与北方向线的夹角,后描述方位即可
∵OA与北方向线的夹角为90°-36°=54°,
∴射线OA所表示的方向是北偏东54°,
故答案为:北偏东54°.
本题考查了方位角,正确理解方位角的意义是解题的关键.
25.105°或75°
【解析】分两种情况:①AB⊥CD,交DC延长线于E,OB交DC延长线于F,②AB⊥CD于G,OA交DC于H求出答案.
解:①如图1,AB⊥CD,交DC延长线于E,OB交DC延长线于F,
∵∠B=45°,∠BEF=90°,
∴∠CFO=∠BFE=45°,
∵∠DCO=60°,
∴∠COF=15°
∴∠AOC=90°+15°=105°;
②如图2,AB⊥CD于G,OA交DC于H,
∵∠A=45°,∠AGH=90°,
∴∠CHO=∠AHG=45°,
∵∠DCO=60°,
∴∠AOC=180°-60°-45°=75°;
故答案为:105°或75°.
此题考查了三角形的角度计算,正确掌握三角板的度数及各角度的关系是解题的关键.
26.120
【解析】设∠BOC=x,则∠AOB=2x,∠AOC=3x,根据角平分线定义求出∠COD,得到方程求出x,即可求出答案.
解:设∠BOC=x,则∠AOB=2x,
∴∠AOC=∠BOC+∠AOB=3x,
∵OD平分∠AOC,
∴∠COD=,
∴,
∴0.5x=20°,
解得x=40°,
∴∠AOC=3x=120°,
故答案为:120.
此题考查了角平分线的定义,角度的和差计算,正确运用角平分线推理论证进行角度的和差计算是解题的关键.
27.
【解析】根据OM平分∠AOC,ON平∠BOD,得到∠MOC=∠AOC,∠DON=∠BOD,结合∠AOB=∠MON+∠MOA+∠NOB,代换计算即可.
∵OM平分∠AOC,ON平∠BOD,
∴∠MOA=∠MOC=∠AOC,∠NOB=∠DON=∠BOD,
∵∠MON=m°,∠COD=n°,∠MON=∠COD +∠MOC +∠DON,
∴∠MOC +∠DON=m-n,
∴∠MOA+∠NOB =m-n,
∴∠AOB=∠MON+∠MOA+∠NOB=m+m-n=2m-n,
故答案为:2m-n.
本题考查了角的平分线即经过角的顶点的射线把角分成相等的两个角,角的和与差的表示,正确理解角的平分线的定义,灵活选择角的和与差是解题的关键.
28.105
【解析】图1中先设∠AOM=x=∠DOM,则∠BOM=60−x,根据∠BOD=∠DOM−∠BOM,得出∠BOD的度数,再根据∠COB=∠BOD+∠DOC,求出∠CON=∠BON,最后根据∠NOM=∠BOM+∠BON,即可得出α; 图2中设∠AOM=∠DOM=x,∠CON=∠BON=y,则∠BOD=60−2x,根据∠AOB=60°,∠COD=45°,列出算式,求出x−y的度数,最后根据∠MON与各角之间的关系,
解:图1中设∠AOM=x=∠DOM,
∵∠AOB=60°,
∴∠BOM=60°−x,
∵∠BOD=∠DOM−∠BOM,
∴∠BOD=x−(60°−x)=2x−60°,
∵∠COB=∠BOD+∠DOC,
∴∠COB=(2x−60°)+45°=2x−15°,
∴∠CON=∠BON=(2x−15°)=x−7.5°,
∴α=∠NOM=∠BOM+∠BON=60°−x+x−7.5°=52.5°;
图2中设∠AOM=∠DOM=x,∠CON=∠BON=y,则∠BOD=60°−2x,
∵∠COD=45°,
∴60−2x+2y=45°,即x−y=7.5°,
∴β=∠MON=x+(60−2x)+y=60−(x−y)=52.5°,
∴=52.5°+52.5°=105°,
故答案为:105.
本题考查了角的计算,解题的关键是设一个未知数(或两个未知数),用代数方法解决几何问题.
29.
【解析】由角平分线的定义可得,结合可求解.
解:平分,平分,
故答案为:.
本题主要考查角的平分线,角的计算,灵活运用角的平分线的定义是解题的关键.
30.33°或53°
【解析】分CA´在∠ACB外部和内部两种情况求解即可.
解:当CA´在∠ACB外部,如图:
∵,,
∴,
∵三角形沿着折叠,
∴,
∴;
当CA´在∠ACB内部,如图:
∵,,
∴,
∵三角形沿着折叠,
∴,
∴;
故答案为:33°或53°
此题考查折叠的性质及角之间的和差,分情况讨论是解答此题的关键.
31.(1)124°
(2)证明见解析
【解析】(1)由题意知,可得的值,然后代入中计算求解即可;
(2)由,,,可得到.
(1)
解:由题意知,
∴
∵
∴.
(2)
证明:∵
∴
∵,
∴
∴平分.
本题考查了角平分线,角度的计算等知识.解题的关键在于找出角度的数量关系.
32.(1)31°3′;(2)见解析;(3)∠BOC=30°.
【解析】(1)根据题意列式计算即可;
(2)根据题意列式计算即可;
(3)设∠AOB=α,则∠AOC=3α,∠COD=4α,得到∠BOD=6α,根据∠BOD=90°,求得α=15°,于是得到∠BOC=90°﹣4×15°=30°.
(1)∵∠M=10°21′,
∴3∠M=3×10°21′=31°3′;
(2)∵∠AOB=∠BOC=∠COD,
∴∠AOC=2∠AOB,∠BOD=2∠AOB;
(3)∵∠AOC是∠AOB的3倍角,∠COD是∠AOB的4倍角,
∴设∠AOB=α,则∠AOC=3α,∠COD=4α,
∴∠AOD=7α,
∴∠BOD=6α,
∵∠BOD=90°,
∴α=15°,
∴∠BOC=90°﹣4×15°=30°.
此题主要考查了角的计算以及余角定义,关键是理清图中角之间的关系,掌握两角和为90°为互余.
33.(1)
(2)
【解析】(1)先根据题意设再根据平角的定义得出方程,解之即可;
(2)先根据角平分线的性质得出,,再根据得出关于的方程即可
(1)解:∵,∴,∵,,∴∴∴
(2)解:∵OM平分,ON平分,
∴,,∴,∵,∴∴
本题主要考查角平分线的定义以及平角的定义,正确找到角的和差倍分关系是解题的关键.
34.(1)4秒;(2)8cm/s或cm/s
【解析】(1)根据点P,Q的运动路程之和为20建立方程求解即可得出结论;
(2)要点P,Q相遇,只能点P运动到线段AB上,判断出点P旋转的角度,进而求出点P的运动时间,即可得出结论.
解:(1)设t秒后,P,Q两点相遇,
根据题意知,(2+3)t=20,
解得,t=4秒,
答:4秒后,P,Q两点相遇.
(2)∵∠POQ=60°,
∴点P绕着点O旋转60°或240°刚好在线段AB,
当点P绕着点O旋转60°时,点P和点Q相遇,
∴点P的旋转了60°÷30°=2秒,
则(20﹣4)÷2=8cm/s,
当点P绕着点O旋转240°时,点P和点Q相遇,
∴点P的旋转了240°÷30°=8秒,
则20÷8=cm/s,
即:点Q的速度为8cm/s或cm/s.
本题主要考查角的和差关系及一元一次方程的应用,熟练掌握角的和差关系及一元一次方程的应用是解题的关键.
35.(1)15°;(2)α;(3)60°或108°
【解析】(1)根据平角的定义即可求出∠BOC,然后根据直角的定义和角平分线的定义即可求出∠DOE;
(2)根据平角的定义即可求出∠BOC,然后根据直角的定义和角平分线的定义即可求出∠DOE;
(3)设∠AOC=α,根据角平分线的定义即可求出∠COE,然后根据OD与直线AB的相对位置分类讨论,分别画出对应的图形,再用α表示出∠DOB即可列出方程,求出结论.
解:(1)由已知得∠BOC=180°-∠AOC=150°
又∵∠COD是直角,OE平分∠BOC
∴∠DOE=∠COD-∠COE=∠COD-∠BOC=90°-×150°=15°
(2)由已知得∠BOC=180°-∠AOC
由(1)知∠DOE=∠COD-∠BOC,
∴∠DOE=90°- (180°-∠AOC)=∠AOC=α
(3)设∠AOC=α,则∠BOC=180°﹣α,
∵OE平分∠BOC,
∴∠COE=×(180°﹣α)=90°﹣α
分两种情况:
当OD在直线AB上方时,∠BOD=90°﹣α,
∵∠COE=2∠DOB,
∴90°﹣α=2(90°﹣α),
解得α=60°
当OD在直线AB下方时,∠BOD=90°﹣(180°﹣α)=α﹣90°,
∵∠COE=2∠DOB,
∴90°﹣α=2(α﹣90°),
解得α=108°.
综上所述,当∠AOC的度数是60°或108°时,∠COE=2∠DOB.
此题考查的是角的和与差,掌握各个角的关系和分类讨论的数学思想是解决此题的关键.
36.120°,∠AOB,∠BOC,40°,120°,160°,∠AOC,80°.
【解析】先求出 的度数,再求出 的度数,根据角平分线定义求出即可.
∵ ,
∴
∴
∵OD平分
∴
故答案为:120°,∠AOB,∠BOC,40°,120°,160°,∠AOC,80°.
本题考查了角平分线的定义以及性质,掌握各角度之间的转换关系是解题的关键.
37.(1)74°;(2)26分钟;(3)20或32
【解析】(1)先根据直角∠EOF,再根据角平分线的定义求出∠AOE,进而由平角定义求解即可;
(2)先求出∠FOD=143°,设x分钟后射线OF与射线OD第一次重合,根据射线OF转动的度数-射线OD转动的度数=143列出方程求解即可;
(3)设两射线同时出发t分钟后,∠FOD=33°,分两条射线第一次重合前和两条射线第一次重合后两种情况,根据题意列出方程求解即可.
解:(1)∵ ∠COE=90°,∠COF=37°,
∴ ∠EOF=90°-37°=53°,
∵ OF 平分∠AOE,
∴ ∠AOE=2∠EOF=53°×2=106°,
∴ ∠EOB=180°-106°=74°;
(2)∵ ∠COD=180°,∠COE=90°,
∴ ∠EOD=90°,
∴ ∠FOD=90°+53°=143°,
设x分钟后射线OF与射线OD第一次重合,
依题意,得:6x-0.5x=143,
解得:x=26.
答:26分钟后,射线OF与射线OD第一次重合;
(3)由(2)可知,开始时∠FOD=143°,
设两射线同时出发t分钟后,∠FOD=33°,
当射线OF与射线OD第一次重合前,根据题意,
得:6t+33=143+0.5t,
解得:t=20;
射线OF与射线OD第一次重合后,根据题意,
得:6t=143+33+0.5t,
解得:t=32,
综上,两射线同时出发20或32分钟后,∠FOD=33°,
故答案为:20或32.
本题考查一元一次方程的应用、角平分线的定义、平角定义、角的运算,理解题意,正确列出一元一次方程是解答的关键,注意分类讨论思想的运用.
38.(1)∠DOF=108°
(2)∠DOF=112.5°
【解析】(1)先由OE⊥AB得出∠AOE=90°,再由角平分线求出∠COF=∠AOC=72°,最后可得∠DOF.
(2)设∠EOF=x°,则∠COE=2x°,∠COF=3x°,再由角平分线求出∠AOF=∠COF=3x°,所以∠AOE=4x°,再由垂直定义列出式子,解出方程即可.
(1)∵OE⊥AB,∴∠AOE=90°;∵∠COE=54°,∴∠AOC=∠AOE+∠COE=144°,∵OF平分∠AOC,∴∠COF=∠AOC=72°,∴∠DOF=180°-∠COF=108°.
(2)设∠EOF=x°,则∠COE=2x°,∴∠COF=3x°,∵OF平分∠AOC,∴∠AOF=∠COF=3x°,∴∠AOE=4x°,∵OE⊥AB,∴∠AOE=90°,∴4x=90,解得x=22.5,∴∠COF=3x°=67.5°,∴∠DOF=180°-∠COF=112.5°.
本题考查了角的计算,根据垂直的定义、角的和差关系列出方程进行求解,难度适中.
39.(1)150°
(2)9或27或45;
(3)t为、、、、
【解析】(1)求出∠AOM及∠BON的度数可得答案;
(2)分两种情况:①当时,②当时,根据OA与OB重合前,OA与OB重合后,列方程求解;
(3)射线OB、射线OM、射线OA中,其中一条射线把另外两条射线的夹角(小于180°)分成2:3的两部分有以下九种情况:
①OA分∠BOM为2:3时,②OA分∠BOM为3:2时,③OB分∠AOM为2:3时,④OB分∠AOM为3:2时,⑤OM分∠AOB为2:3时,⑥ OB分∠AOM为2:3时,⑦OB分∠AOM为3:2时,⑧ OA分∠BOM为3:2时,⑨ OA分∠BOM为2:3时,列方程求解并讨论是否符合题意.
(1)
解:当t=3时,∠AOM=12°,∠BON=18°,
∴∠AOB=180°-∠AOM-∠BON=150°,
故答案为:150°;
(2)
解:分两种情况:
①当时,
当OA与OB重合前,,得t=9;
当OA与OB重合后,,得t=27;
②当时,
当OA与OB重合前,,得t=45;
当OA与OB重合后,,得t=63(舍去);
故t的值为9或27或45;
(3)
解:射线OB、射线OM、射线OA中,其中一条射线把另外两条射线的夹角(小于180°)分成2:3的两部分有以下九种情况:
①OA分∠BOM为2:3时,
∴4t:(180-4t-6t)=2:3,
解得:t=;
②OA分∠BOM为3:2时,
∴4t:(180-4t-6t)=3:2,
解得:t=;
③OB分∠AOM为2:3时,
∵,
∴,
得t=;
④OB分∠AOM为3:2时,
∴,
得t=;
⑤OM分∠AOB为2:3时,
∴,
得t=54,
此时>180°,故舍去;
⑥ OB分∠AOM为2:3时,
∴,
得,
此时,故舍去;
⑦OB分∠AOM为3:2时,
∴,
得,
此时,故舍去;
⑧ OA分∠BOM为3:2时,
∴,
得,
⑨ OA分∠BOM为2:3时,
∴,
得t=67.5(舍去)
综上,当t的值分别为、、、、时,射线OB、射线OM、射线OA中,其中一条射线把另外两条射线的夹角(小于180°)分成2:3的两部分.
此题考查了角的计算,角的旋转,几何图形中角度的度数比,列一元一次方程,正确画出图形求角度值是解题的关键.
40.30°或150°
41.45°
42.45°
【解析】(1)画出符合条件的两种情况,①当射线OC在∠AOB内部时,②当射线OC在∠AOB外部时,分别求出即可;
(2)画出符合条件的两种情况,①当射线OC在∠AOB内部,②当射线OC在∠AOB外部,求出即可;
(3)画出符合条件的两种情况,求出∠COD和∠COE的度数,即可求出答案.
40.分为两种情况:
①如图1,
当射线OC在∠AOB内部时,
∠COB=∠AOB﹣∠AOC=90°﹣60°=30°;
②如图2,
当射线OC在∠AOB外部时,
∠COB=∠AOB+∠AOC=90°+60°=150°;
故答案为:30°或150°;
41.在图3中,
∵∠AOB=90°,∠AOC=60°,OD平分∠BOC,OE平分∠AOC,
∴∠DOC=∠BOC=×30°=15°,∠COE=∠AOC=×60°=30°,
∴∠DOE=∠COD+∠COE=15°+30°=45°;
在图4中,
∵∠AOB=90°,∠AOC=60°,OD平分∠BOC,OE平分∠AOC,
∴∠DOC=∠BOC=×(90°+60°)=75°,∠COE=∠AOC=×60°=30°,
∴∠DOE=∠COD﹣∠COE=75°﹣30°=45°;
故答案为:45°;
42.能求出∠DOE的度数.
①当OC在∠AOB内部时,如图3,
∵∠AOB=90°,∠AOC=2α°,
∴∠BOC=∠AOB﹣∠AOC=90°﹣2α°,
∵OD、OE分别平分∠BOC,∠AOC,
∴∠DOC=∠BOC=45°﹣α°,∠COE=∠AOC=α°,
∴∠DOE=∠DOC+∠COE=(45°﹣α°)+α°=45°;
②当OC在∠AOB外部时,如图4,
∵∠AOB=90,∠AOC=2α°,
∴∠BOC=∠AOB+∠AOC=90°+2α°,
∵OD、OE分别平分∠BOC,∠AOC,
∴∠DOC=∠BOC=45°+α°,∠COE=∠AOC=α°,
∴∠DOE=∠DOC﹣∠COE=(45°+α°)﹣α°=45°;
综合上述,∠DOE=45°.
本题考查了角的计算,角平分线的定义,熟练掌握知识点并能够分类讨论是解题的关键.
43.(1)
(2)或
【解析】(1)根据角的三等分线的意义进行计算求解;
(2)根据角平分线的定义和角的三等分线的意义,分两种情况进行计算求解.
(1)
解:,OC是的一条三等分线,且,
;
(2)
解:,OC是的一条三等分线,且,
,.
∵OE是的角平分线,OF是∠AOB的角平分线,
∴,,
,
.
设旋转后的角为,旋转的时间为t秒,
如图2-1,当OB是的一条三等分线,且时,
,
,
,
解得(秒);
如图2-2,当OB是的一条三等分线,且时,
,
,
,
解得(秒),
当秒或秒时,射线OB恰好是的一条三等分线.
本题考查了角平分线的定义,理解角平分线、角三等分线的意义是正确解答的前提.
44.(1)
(2)秒或秒,秒或秒,秒或秒
(3)分钟或分钟
【解析】(1)根据同角的余角相等可得;
(2)根据路程等于速度乘以时间分别求得运动到所需要的时间,进而求得停止的时间,根据角度的和差可得,根据角度的方向以及角平分线的定义,建立绝对值方程,解方程求解即可;
(3)根据题意作出图形,类比(2)建立方程,在周角内求角度,进而解方程求解即可.
(1)
OB⊥OD,OA⊥OC,
∠COD=40°
故答案为:
(2)
设旋转时间为秒,
当旋转至所需要的时间为:(秒)
当旋转至所需要的时间为:(秒)
当旋转至所需要的时间为:(秒)
当旋转至时,其他线段都停止,则,
旋转秒后,,,
,
,
①当平分时,,
即或
解得:或
②当平分时,,
即或
解得:或
③当平分时,,
即或
解得:或
综上所述,或,或,或
(3)
如图,
根据题意,6时整时,,
6时至7时,旋转了30°,旋转了360°
则的速度为度/分钟,的速度为度/分钟,
6点整之后,设分钟后,
则
或
解得:或
本题考查了角度的旋转,几何图形中角度的计算,一元一次方程的应用,钟表角的计算,根据题意建立一元一次方程是解题的关键.
45.(1)40
(2)①存在,秒或44秒;②,30,,
【解析】(1)根据“友好线”的含义即可完成;
(2)①分两种情况:OC与OD相遇之前,根据180゜减去OC、OD旋转的角度的和等于40度列出方程即可;OC与OD相遇之后,根据OC、OD旋转的角度的和减去180゜等于40゜列出方程即可;
②分相遇前与相遇后两种情况:相遇前又分两种情况:是的“友好线”;是的“友好线”;相遇后也分两种情况:是的“友好线”;是的“友好线”;根据“友好线”的含义即可求得t的值.
(1)
∵射线是射线的“友好线”,且
∴
故答案为:;
(2)
射线与重合时,(秒)
①存在
当的度数是时,∠AOC=,
有两种可能:
若在相遇之前,则,即,
;
若在相遇之后,则,即,
;
综上所述,当秒或44秒时,的度数是.
②相遇之前:
(I)如图1,
是的“友好线”时,则,
即,
(II)如图2,
是的“友好线”时,则,
即,
相遇之后:
(III)如图3,
是的“友好线”时,则
即,
(Ⅳ)如图4,
是的“友好线”时,则
即,
所以,综上所述,当,30,,时,、、OA中恰好有一条射线是另一条射线的“友好线”.
本题是材料阅读题,考查了角的运算,解一元一次方程等知识,读懂题目提供的材料,正确分类解决是本题的关键.
46.(1)是;(2)①9或12或18;②或或
【解析】(1)根据奇妙线定义即可求解;
(2)①分3种情况,ÐQPN=2ÐMPN;ÐMPN=2ÐQPM;ÐQPM =2ÐMPN.列出方程求解即可;
②分3种情况,ÐMPN=2ÐQPN;ÐMPQ=2ÐQPN;ÐQPN =2ÐMPQ.列出方程求解即可.
(1)设∠α被角平分线分成的两个角为∠1和∠2,
则有∠α=2∠1,
∴一个角的平分线是这个角的“奇妙线”;
故答案是:是;
(2)①由题意可知射线 PM 在ÐQPN的内部,
∴ÐQPN=(10t)°,ÐQPM=(10t-60)°,
(a)当ÐQPN=2ÐMPN时,
10t=2×60,
解得t=12;
(b)当ÐMPN=2ÐQPM时,
60=2×(10t-60),
解得t=9;
(c)当ÐQPM =2ÐMPN时,
(10t-60)=2×60,
解得t=18.
故当t为9或12或18时,射线PM是∠QPN的“奇妙线”;
②由题意可知射线 PQ 在ÐMPN的内部,
∴ÐQPN=(10t)°,ÐMPN=(60+6t)°,ÐQPM=ÐMPN-ÐQPN=(60-4t)°,
(a)当ÐMPN=2ÐQPN时,
60+6t=2×10t,
解得t=;
(b)当ÐMPQ=2ÐQPN时,
60-4t=2×10t,
解得t=;
(c)当ÐQPN =2ÐMPQ时,
10t=2×(60-4t),
解得t=.
故当射线PQ是∠MPN的奇妙线时t的值为或或.
本题考查了角之间的关系及一元一次方程的应用,奇妙线定义,学生的阅读理解能力及知识的迁移能力.理解“奇妙线”的定义是解题的关键.
47.(1)是
(2)n
(3)或或或或秒
【解析】(1)根据“友好线”定义即可作出判断;
(2)根据“友好线”定义即可求解;
(3)利用分类讨论思想,分别作出图形,分情况进行计算即可.
(1)
解:∵OB是∠BOC的平分线,
∴∠BOD=∠COD,
∵∠COA=∠BOC,
∴∠BOD=∠AOD,
∴射线OD是射线OB在∠AOB内的一条“友好线”.
故答案为:是.
(2)
∵射线OM是射线OB在∠AOB内的一条“友好线”,∠AOB的度数为n,
∴∠BOM=∠AOB=n,
∵ON平分∠AOB,
∴∠BON=∠AOB=n,
∴∠MON=∠BON﹣∠BOM=n﹣n=n.
故答案为:n.
(3)
设运动时间为x秒时,射线OA、OB、OC中恰好有一条射线是其余两条射线中某条射线的“友好线”.
当射线OC与射线OA的延长线重合时,运动停止
如图,当射线OC是射线OA在∠AOB内的一条“友好线”时,当时,
根据题意可得,,则
解得
如图,当射线OC是射线OB在∠AOB内的一条“友好线”时,当时,
,,
解得
即运动时间为秒时,射线OC是射线OB的“友好线”.
③如图,当射线OB是射线OA在∠AOC内的一条“友好线”时,则∠AOB=∠COB,
,,
所以10+x=,
解得x=(符合题意),
即运动时间为秒时,射线OB是射线OA的“友好线”.
④如图,当射线OB是射线OC在∠AOC内的一条“友好线”时,则∠AOB=∠COB,
,,
解得
⑤如图,,
当时
解得:
当时
解得:
综上所述,当运动时间为或或或或秒时,符合题意要求.
本题考查了一元一次方程的应用,角的计算,解决本题的关键是利用分类讨论思想.
48.(1)4;144°,114°;(2)t的值为10s;(3)当射线OM在∠COB内部,且是定值时,t的取值范围为<t<6,这个定值是3
【解析】(1)由直线AB,CD相交于点O,∠AOC=∠AOD即可得到共4个直角;当t=2时求得∠BOM=30°,∠NON=24°,即可得到∠MON、∠BON的度数;
(2)用t分别表示出∠BOM=15t,∠NOD=12t,∠COM=15t﹣90°,根据OE平分∠COM,OF平分∠NOD,分别求得∠COE、∠DOF,由∠EOF为直角即∠COE+∠DOF=90°,列出方程解答即可.
(3)先确定∠MON=180°时,∠BOM=90°时t的值,再分两种情况进行计算,得到0<t<时不是定值,当<t<6时,=3是定值.
(1)如图所示,∵两条直线AB,CD相交于点O,∠AOC=∠AOD,
∴∠AOC=∠AOD=90°,
∴∠BOC=∠BOD=90°,
∴图中一定有4个直角;
当t=2时,∠BOM=30°,∠NON=24°,
∴∠MON=30°+90°+24°=144°,
∠BON=90°+24°=114°;
故答案为:4;144°,114°;
(2)如图所示,∠BOM=15t,∠NOD=12t,∠COM=15t﹣90°,
∵OE平分∠COM,OF平分∠NOD,
∴∠COE=∠COM=(15t﹣90°),∠DOF=∠DON=×12t,
∵当∠EOF为直角时,∠COE+∠DOF=90°,
∴(15t﹣90°)=×12t,
解得t=10,
∴当∠EOF为直角时,t的值为10s;
(3)当∠MON=180°时,∠BOM+∠BOD+∠DON=180°,
∴15t+90°+12t=180°,
解得t=,
当∠BOM=90°时,15t=90°,
解得t=6,
①如图所示,当0<t<时,
∠COM=90°﹣15t,∠BON=90°+12t,
∠MON=∠BOM+∠BOD+∠DON=15t+90°+12t,
∴=,(不是定值)
②如图所示,当<t<6时,
∠COM=90°﹣15t,∠BON=90°+12t,
∠MON=360°﹣(∠BOM+∠BOD+∠DON)=360°﹣(15t+90°+12t)=270°﹣27t,
∴==3,(是定值)
综上所述,当射线OM在∠COB内部,且是定值时,t的取值范围为<t<6,这个定值是3.
此题考察图形中的运动问题,(3)先确定∠MON=180°时,∠BOM=90°时t的值,再分两种情况进行计算,得到0<t<时不是定值,当<t<6时,=3是定值.
初中数学6.2 一次函数课后作业题: 这是一份初中数学6.2 一次函数课后作业题,共8页。
初中数学苏科版七年级上册6.3 余角 补角 对顶角随堂练习题: 这是一份初中数学苏科版七年级上册6.3 余角 补角 对顶角随堂练习题,共30页。试卷主要包含了下列说法中等内容,欢迎下载使用。
初中数学苏科版七年级上册6.1 线段 射线 直线同步练习题: 这是一份初中数学苏科版七年级上册6.1 线段 射线 直线同步练习题,共39页。