初中数学人教版九年级上册24.1.3 弧、弦、圆心角备课课件ppt

这是一份初中数学人教版九年级上册24.1.3 弧、弦、圆心角备课课件ppt，共28页。PPT课件主要包含了教学目标，教学重难点，回顾旧知，情境引入，圆是中心对称图形，顶点在圆心上，合作学习，圆心角的概念，圆心角，圆内角等内容，欢迎下载使用。

把一个图形绕某一个点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形叫做中心对称图形，这个点就是它的对称中心.
★中心对称图形的定义:
1、说一说什么是中心对称图形？
2、圆是中心对称图形吗？
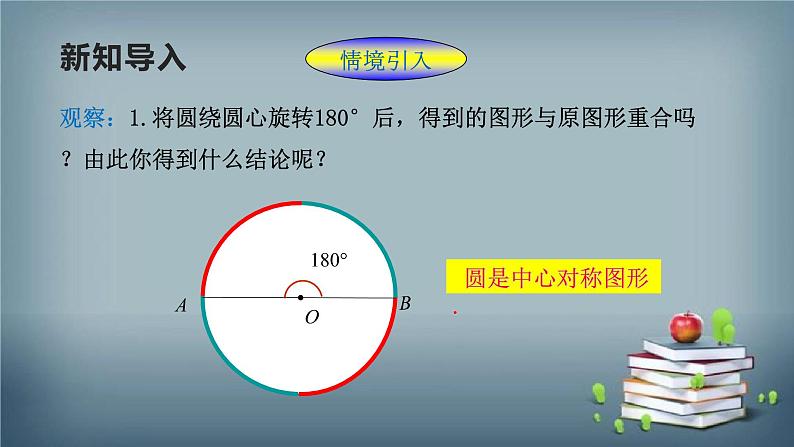
圆是中心对称图形，就是它的旋转中心。
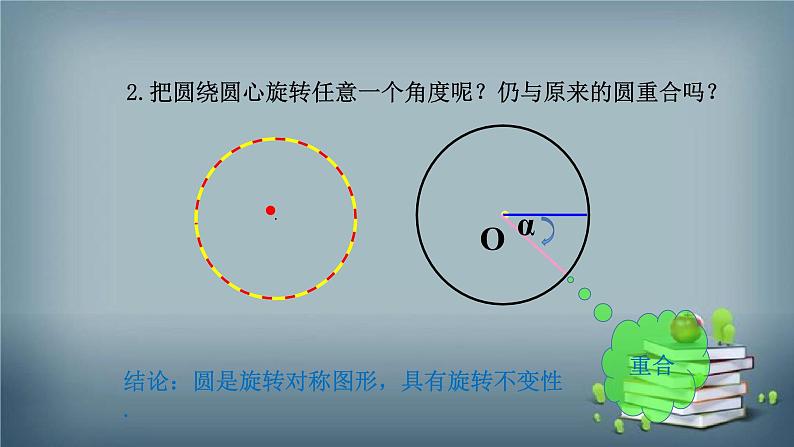
不仅如此，把圆绕圆心旋转任意角度，所得的图形都与原图形重合。
观察：1.将圆绕圆心旋转180°后，得到的图形与原图形重合吗？由此你得到什么结论呢？
2.把圆绕圆心旋转任意一个角度呢？仍与原来的圆重合吗？
结论：圆是旋转对称图形，具有旋转不变性.
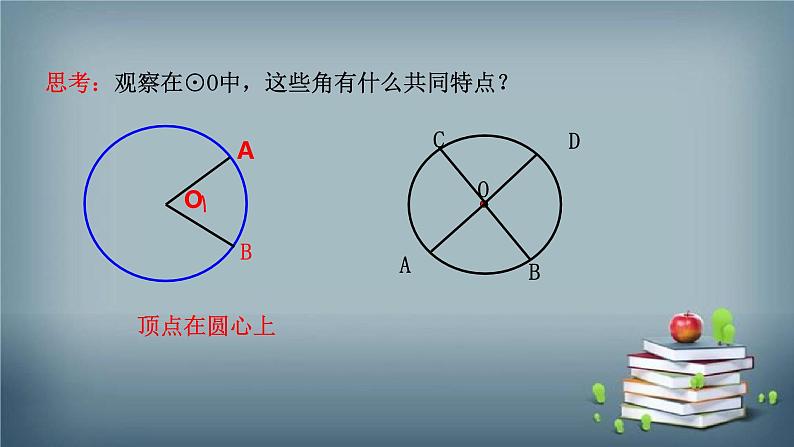
思考：观察在⊙O中，这些角有什么共同特点？
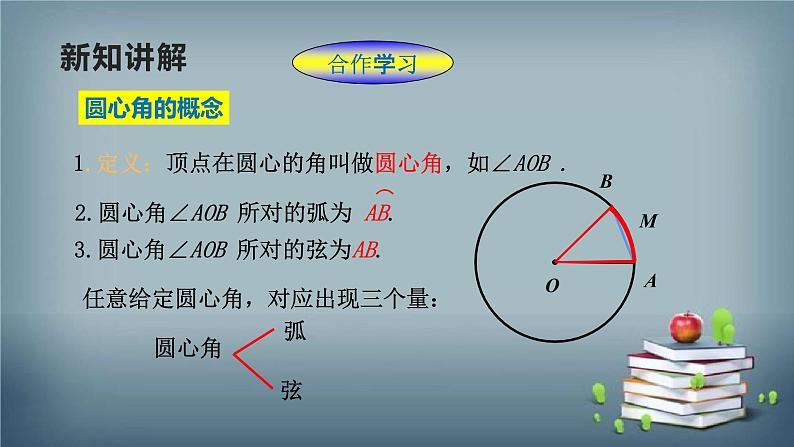
1.定义：顶点在圆心的角叫做圆心角，如∠AOB .
3.圆心角∠AOB 所对的弦为AB.
任意给定圆心角，对应出现三个量：
判一判：判断下列各图中的角是不是圆心角，并说明理由.
圆心角与所对的弧、弦之间的关系
思考：如图，将圆心角∠AOB绕圆心O旋转到∠A1OB1的位置，你能发现哪些等量关系？为什么？
∵ ∠AOB=∠A1OB1
如图，⊙O与⊙O1是等圆，∠AOB =∠A1OB1=60°，请问上述结论还成立吗？为什么?
在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等．
思考：这句话“相等的圆心角所对的弧相等，所对的弦也相等．”对吗？为什么？
强调：必须在“在同圆或等圆中”前提条件下，结论才成立.
在同圆或等圆中，如果两条弧相等，那么它们所对的圆心角相等，所对的弦相等．
强调：如果条件为“两条弧相等”，那么“在同圆或等圆中”这个前提条件可以省略了.
在同圆或等圆中，如果两条弦相等，那么它们所对的圆心角相等，所对的优弧和劣弧分别相等．
在同圆或等圆中，如果两条弧相等，那么它们所对的圆心角相等，所对的弦相等．
弧、弦与圆心角关系定理的推论：
在同圆或等圆中，如果两条弦相等，那么它们所对的圆心角相等，所对的优弧和劣弧分别相等．
思考：在同圆或等圆中，两个圆心角、两条弧、两条弦中如果有一组量相等，那么它们所对应的其余各组量有什么关系？
∴ AB=AC．△ABC是等腰三角形.
∴ △ABC是等边三角形 , AB=BC=CA.
∴ ∠AOB＝∠BOC＝∠AOC.
本题中弧、圆心角、弦灵活转化是解题的关键.还要注意前提条件（在同圆或等圆中）.
温馨提示：一条弦对应两条弧，由弦相等得到弧相等时需要区分优弧和劣弧.
1．如果两个圆心角相等，那么（ ） A．这两个圆心角所对的弦相等 B．这两个圆心角所对的弧相等 C．这两个圆心角所对的弦的弦心距相等 D．以上说法都不对
3.如图，AB、CD是⊙O的两条弦．（1）如果AB=CD，那么_________，__________ __；（2）如果 ，那么_________， ；（3）如果∠AOB=∠COD，那么_________，_______；
证明 连接OC.
∴∠BOD=∠COD.
∵∠COB=∠A+∠C=∠COD+∠BOD，
∴∠A=∠C=∠COD=∠BOD，
即∠AOE=∠BOF，
证明 ∵OC=OD，
∴∠OCD=∠ODC.
∴∠OAC=∠OBD，
∴∠OCD-∠OAC=∠ODC-∠OBD，
∴∠AOC=∠BOD，
今天我们学习了哪些知识？
弦、弧、圆心角的关系定理
①要注意前提条件；②要灵活转化.