浙江省宁波市鄞州区3年（2020-2022）八年级数学上学期期末试题汇编2填空题

浙江省宁波市鄞州区3年（2020-2022）八年级数学上学期期末试题汇编02 填空题

二、填空题

31．（2019·浙江宁波·八年级期末）“内错角相等，两直线平行”的逆命题是_____．

32．（2019·浙江宁波·八年级期末）若函数y=2x+b（b为常数）的图象经过点A（0，﹣2），则b=_____．

33．（2019·浙江宁波·八年级期末）三角形两边长分别是2，4，第三边长为偶数，第三边长为_______

34．（2019·浙江宁波·八年级期末）点M（a+b，ab）在第二象限，那么点N（a，b）在第_______象限.

35．（2019·浙江宁波·八年级期末）等腰三角形的一腰上的高与另一腰所在直线的夹角为40°，则这个三角形的底角为_____．

36．（2019·浙江宁波·八年级期末）如图，在中，，，，现将沿进行翻折，使点刚好落在上，则__________．

37．（2019·浙江宁波·八年级期末）在直角坐标系中，有A（3，－3），B（5，3）两点，现另取一点C（1，n），当△ABC周长最小时，n的值是___．

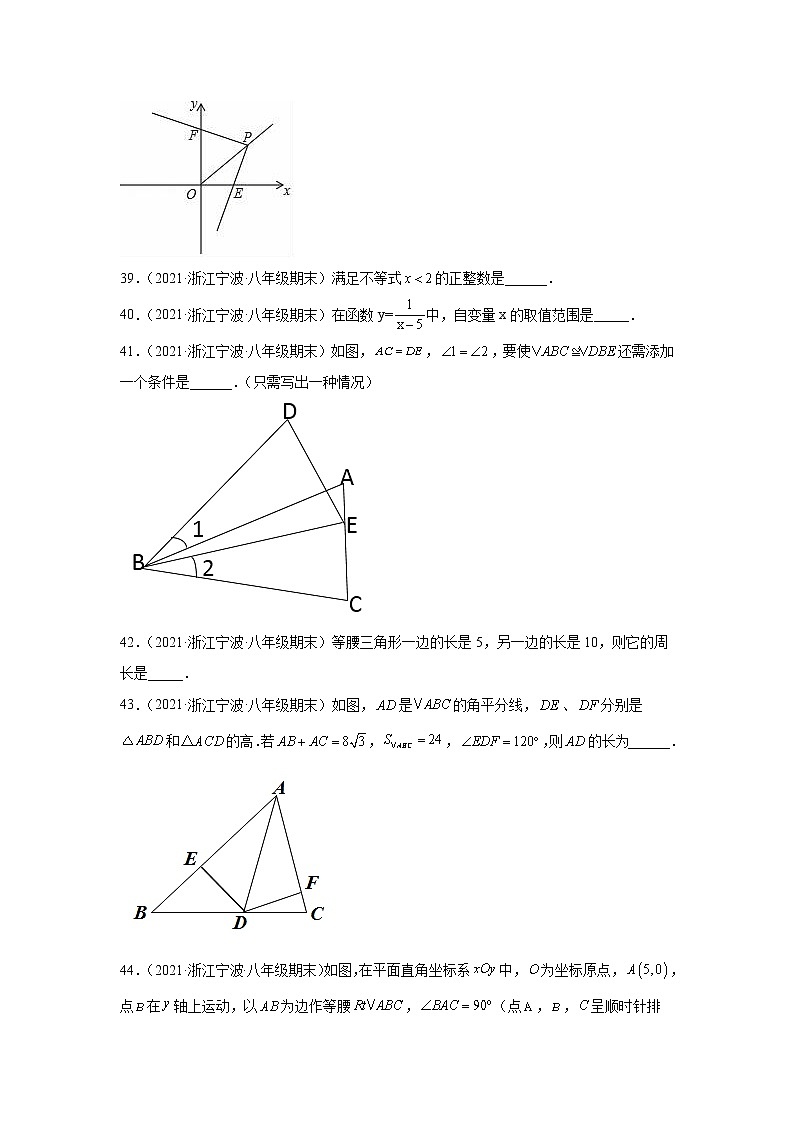
38．（2019·浙江宁波·八年级期末）如图，在平面直角坐标系中，P是第一象限角平分线上的一点，且P点的横坐标为3．把一块三角板的直角顶点固定在点P处，将此三角板绕点P旋转，在旋转的过程中设一直角边与x轴交于点E，另一直角边与y轴交于点F，若△POE为等腰三角形，则点F的坐标为_____．

39．（2021·浙江宁波·八年级期末）满足不等式的正整数是______．

40．（2021·浙江宁波·八年级期末）在函数y=中，自变量x的取值范围是_____．

41．（2021·浙江宁波·八年级期末）如图，，，要使还需添加一个条件是______．（只需写出一种情况）

42．（2021·浙江宁波·八年级期末）等腰三角形一边的长是5，另一边的长是10，则它的周长是_____．

43．（2021·浙江宁波·八年级期末）如图，是的角平分线，、分别是和的高．若，，，则的长为______．

44．（2021·浙江宁波·八年级期末）如图，在平面直角坐标系中，为坐标原点，，点在轴上运动，以为边作等腰，（点，，呈顺时针排列），当点在轴上运动时，点也随之运动．在点的运动过程中，的最小值为______．

45．（2020·浙江宁波·八年级期末）请写出“全等三角形的面积相等”的逆命题___．

46．（2020·浙江宁波·八年级期末）函数的自变量的取值范围是________．

47．（2020·浙江宁波·八年级期末）若实数,则x可取的最大整数是_______．

48．（2020·浙江宁波·八年级期末）等腰三角形的一个外角度数为100°，则顶角度数为_____．

49．（2020·浙江宁波·八年级期末）如图，D为△ABC外一点，BD⊥AD，BD平分△ABC的一个外角，∠C=∠CAD，若AB=5，BC=3，则BD的长为_______．

50．（2020·浙江宁波·八年级期末）如图，Rt△ABC中，∠C=90°，∠BAC的角平分线AE与AC的中线BD交于点F，P为CE中点，连结PF，若CP=2，，则AB的长度为_______．

【答案】

31．两直线平行，内错角相等

【分析】把一个命题的条件和结论互换就得到它的逆命题．

【详解】“内错角相等，两直线平行”的逆命题是“两直线平行，内错角相等”．

故答案为：两直线平行，内错角相等

32．-2

【详解】∵函数图象经过点A(0，﹣2)，

∴﹣2=2×0+b，

得b=﹣2.

故答案为:﹣2

33．4

【详解】设第三边为a，根据三角形的三边关系知，4-2＜a＜4+2．

即2＜a＜6，

∵第三边长为偶数，

∴a=4．

故答案为：4

34．三

【详解】试题分析：∵点M（a+b，ab）在第二象限，

∴ab＞0，a+b＜0，

∵ab＞0，

∴a、b同号，

∵a+b＜0，

∴a＜0，b＜0，

∴点（a，b）在第三象限．

故答案是三．

考点：点的坐标．

35．65°或25°；

【分析】本题已知没有明确三角形的类型，所以应分这个等腰三角形是锐角三角形和钝角三角形两种情况讨论．

【详解】解：当这个三角形是锐角三角形时：高与另一腰的夹角为40，则顶角是50°，因而底角是65°；

当这个三角形是钝角三角形时：高与另一腰的夹角为40°，则顶角的外角是50°，则底角是25°．

因此这个等腰三角形的一个底角的度数为25°或65°．

故填25°或65°．

【点睛】本题考查了等腰三角形的性质及三角形内角和定理；等腰三角形的高线，可能在三角形的内部，边上、外部几种不同情况，因而，遇到与等腰三角形的高有关的计算时应分类讨论．

36．

【详解】解：设CD=x，则AD=A′D=4-x．

在直角三角形ABC中，BC==5．

则A′C=BC-AB=BC-A′B=5-3=2．

在直角三角形A′DC中：AD2+AC2=CD2．

即：（4-x）2+22=x2．

解得：x=．

故答案为：2.5

37．-1

【分析】先作出点A关于的对称点，再连接，求出直线的表达式，再把代入求解即可．

【详解】解：作点A关于的对称点，连接，交于点C，

此时的值最小，

设直线的表达式为，

把和B（5，3）代入得：，

解得：，

∴直线的表达式为，

把C（1，n）代入得，

故答案为：-1．

【点睛】此题考查了轴对称—最短路径问题，解题的关键是根据题意作出点A关于的对称点进而求出直线的表达式．

38．（0，0）或（0，3）或（0，6﹣3）或（0，6+3）．

【分析】根据题意，结合图形，分情况讨论：

①PE=OE；

②OP=PE；

③OP=OE．

【详解】解：△POE是等腰三角形的条件是：OP、PE、EO其中两段相等，P（3，3），那么有：

①当PE=OE时，PE⊥OC，

则PF⊥y轴，则F的坐标是（0，3）；

②当OP=PE时，∠OPE=90°，则F点就是（0，0）；

③当OP=OE时，则OF=6±3

F的坐标是：（0，6-3）或（0，6+3）．

【点睛】本题考查综合应用点的坐标、等腰三角形的判定等知识进行推理论证、运算及探究的能力．

39．1

【分析】根据不等式和正整数的概念，直接求解即可．

【详解】满足不等式的正整数是：1．

故答案是：1．

【点睛】本题主要考查一元一次不等式，理解不等式的意义，是解题的关键．

40．.

【详解】求函数自变量的取值范围，就是求函数解析式有意义的条件，根据分式分母不为0的条件，要使在实数范围内有意义，必须.

41．∠A＝∠D

【分析】由，可得∠ABC=∠DBE，再根据全等三角形的判定定理，即可得到答案．

【详解】解：添加条件为∠A＝∠D，理由是：

∵，

∴∠ABC=∠DBE，

在△ABC和△DBE中，

，

∴（AAS），

故答案为：∠A＝∠D．

【点睛】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．

42．25

【分析】分类讨论：腰为5或腰为10，然后根据等腰三角形的性质得到第三边，再满足三角形三边的关系，最后根据三角形的周长的定义计算即可．

【详解】解：若腰为5，则5+5＝10，不满足三角形三边关系，舍去；

若腰为10，则它的周长＝10+10+5＝25．

故答案为25．

【点睛】本题考查了等腰三角形的性质：等腰三角形的两腰相等．也考查了三角形三边的关系．

43．

【分析】先证明△ADE≌△ADF，可得：DE＝DF，∠ADE＝∠ADF＝=×120°=60°，再利用面积法求出DE的值，再根据直角三角形的性质即可解决问题．

【详解】解：∵DE、DF分别是△ABD和△ACD的高，

∴∠AED＝∠AFD＝90°，

∵AD是△ABC的角平分线，

∴∠DAE＝∠DAF，

∵AD＝AD，

∴△ADE≌△ADF（AAS），

∴DE＝DF，∠ADE＝∠ADF＝=×120°=60°，

∴S△ABC＝•AB•DE＋•AC•DF＝•DE（AB＋AC）＝24，

∵，

∴DE＝，

∵∠ADE＝∠ADF＝60°，

∴∠DAE＝30°，

∴AD＝2DE＝．

故答案是：．

【点睛】本题考查全等三角形的判定和性质，直角三角形的性质，角平分线等知识，解题的关键是正确寻找全等三角形解决问题，学会利用面积法解决问题，属于中考常考题型．

44．

【分析】过点A作直线l⊥x轴，过C，B作CD⊥l于点D，BE⊥l于点E，易证∆CDA≅∆ AEB，从而得AD=BE=OA=5，作点A关于CD的对称点A′，由三角形三边长关系得：当O，C，A′三点共线时，有最小值=OA′，利用勾股定理即可求解．

【详解】如图，过点A作直线l⊥x轴，过C，B作CD⊥l于点D，BE⊥l于点E，

∵∠DCA+∠CAD=90°，∠EAB+∠CAD=180°-90°=90°，

∴∠DCA=∠EAB，

又∵∠CDA=∠AEB=90°，AB=AC，

∴∆CDA≅∆ AEB（AAS），

∴BE=AD，

∵，

∴AD=BE=OA=5，

作点A关于CD的对称点A′，连接CA′，则点A′在直线l上，DA′=DA=5，AC=A′C，

∴=OC+A′C，

∵在∆COA′中，OC+A′C≥OA′，

∴当O，C，A′三点共线时，有最小值=OA′，此时，OA′=，

∴最小值=．

故答案是：．

【点睛】本题主要考查全等三角形的判定和性质，勾股定理，利用轴对称求线段和的最小值问题，添加合适的辅助线，构造直角三角形，是解题的关键．

45．面积相等的两个三角形全等

【分析】根据逆命题的概念可直接进行求解．

【详解】解：“全等三角形的面积相等”的逆命题为面积相等的两个三角形全等；

故答案为：面积相等的两个三角形全等．

【点睛】本题主要考查逆命题，熟练掌握逆命题的概念：把原命题的结论作为命题的条件，把原命题的条件作为命题的结论，所组成的命题叫做原命题的逆命题．

46．x≠1

【详解】解：因为分式的分母不为0，

所以x－1≠0,即x≠1

故答案为：x≠1．

47．2

【分析】根据 ，得出x可取的最大整数是2

【详解】∵

∴x可取的最大整数是2

【点睛】本题考查了无理数的大小比较，通过比较无理数之间的大小可得出x的最大整数值

48．80°或20°

【详解】解：若顶角的外角是100°，则顶角是80°；

若底角的外角是100°，则底角是80°，顶角是20°．

故答案为：80°或20°．

49．3

【分析】延长AD与BC交于点E，求出AB和AD的长，再利用勾股定理求出BD的长

【详解】如图，设CB与AD延长线交于E点

∵BD平分∠ABE，

在直角△ABD中，由勾股定理得到

【点睛】本题考查了辅助线以及勾股定理的运用，利用辅助线求出直角三角形直角边和斜边长，再利用勾股定理求出直角边长是关键

50．15

【分析】作辅助线交AB于H，再利用等量关系用△BFP的面积来表示△BEA的面积，利用三角形的面积公式来求解底边AB的长度

【详解】作

∵AE平分∠BAC

∵P为CE中点

∵D为AC中点，P为CE中点

【点睛】本题考查了辅助线的运用以及三角形的中线平分三角形的面积，解题的关键在于如何利用△BFP的面积来表示△BEA的面积