初中数学北师大版八年级上册第三章 位置与坐标综合与测试练习题

这是一份初中数学北师大版八年级上册第三章 位置与坐标综合与测试练习题，共32页。试卷主要包含了单选题，填空题等内容，欢迎下载使用。

专题3.4 《位置与坐标》全章复习与巩固（培优篇）
（专项练习）
一、单选题
1．对平面上任意一点(a，b)，定义f，g两种变换：f(a，b)＝(﹣a，b)，如f(1，2)＝(﹣1，2)；g(a，b)＝(b，a)，如g(1，2)＝(2，1)，据此得g[f(5，﹣9)]＝（　　）
A．(5，﹣9) B．(﹣5，﹣9) C．(﹣9，﹣5) D．(﹣9，5)
2．在平面直角坐标系中，对于点，我们把点叫做点伴随点．已知点的伴随点为，点的伴随点为，点的伴随点为，…，这样依次得到点，，，…，，…．若点的坐标为，点的坐标为（       ）
A． B． C． D．
3．已知点位于第二象限，并且，a，b均为整数，则满足条件的点A个数有（       ）
A．4个 B．5个 C．6个 D．7个
4．已知点E（x0，yo），点F（x2．y2），点M（x1，y1）是线段EF的中点，则x1＝，y1＝．在平面直角坐标系中有三个点A（1，﹣1），B（﹣1，﹣1），C（0，1），点P（0，2）关于点A的对称点P1（即P，A，P1三点共线，且PA＝P1A），P1关于点B的对称点P2，P2关于点C的对称点P3，…按此规律继续以A，B，C三点为对称点重复前面的操作．依次得到点P4，P5，P6…，则点P2020的坐标是（　　）
A．（4，0） B．（﹣2，2） C．（2，﹣4） D．（﹣4，2）
5．在平面直角坐标系xOy中，点A（0，2），B（a，0），C（m，n），其中m＞a，a＜1，n＞0，若△ABC是等腰直角三角形，且AB＝BC，则m的取值范围是（　　）
A．0＜m＜2 B．2＜m＜3 C．m＜3 D．m＞3
6．如图，在平面直角坐标系中，已知点A（1，0），B（1﹣a，0），C（1+a，0）（a＞0），点P在以D（4，4）为圆心，1为半径的圆上运动，且始终满足∠BPC=90°，则a的最大值是（     ）

A．3 B．4 C．5 D．6
7．如图，在平面直角坐标系中，∠AOB=30°，点A的坐标为(2，0)，过点A作AA1⊥OB，垂足为点A1，过A1作A1A2⊥x轴，垂足为点A2；再过点A2作A2A3⊥OB，垂足为点A3；再过点A3作A3A4⊥x轴，垂足为点A4…；这样一直作下去，则A2017的横坐标为(　　)

A． •()2015 B． •()2016 C． •()2017 D． •()2018
8．如图，阴影部分组成的图案既是关于x轴成轴对称的图形又是关于坐标原点O成中心对称的图形．若点A的坐标是（1，3），则点M和点N的坐标分别是（ ）

A．M（1，﹣3），N（﹣1，﹣3）
B．M（﹣1，﹣3），N（﹣1，3）
C．M（﹣1，﹣3），N（1，﹣3）
D．M（﹣1，3），N（1，﹣3）
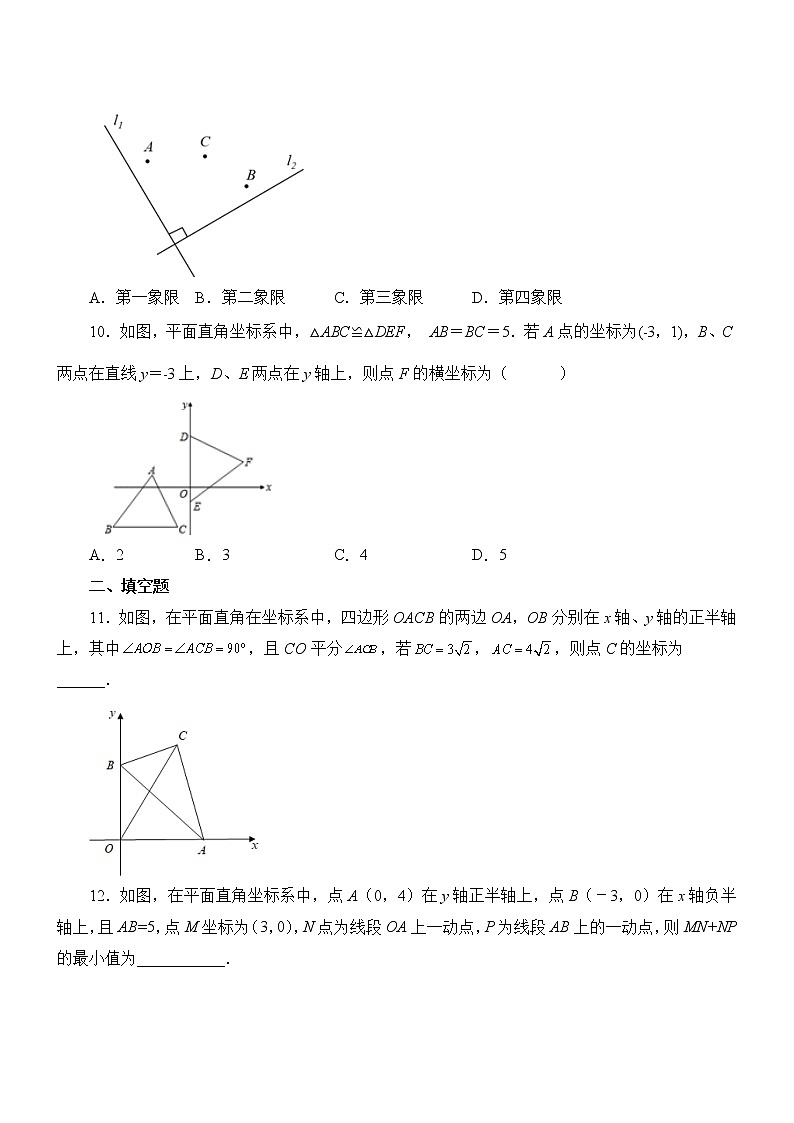
9．如图，已知直线l1⊥l2，且在某平面直角坐标系中， x轴∥l1，y轴∥l2，若点A的坐标为(-1，2)，点B的坐标为(2，-1)，则点C在(        )

A．第一象限 B．第二象限 C．第三象限 D．第四象限
10．如图，平面直角坐标系中，△ABC≌△DEF， AB＝BC＝5．若A点的坐标为(﹣3，1)，B、C两点在直线y＝﹣3上，D、E两点在y轴上，则点F的横坐标为（        ）

A．2 B．3 C．4 D．5
二、填空题
11．如图，在平面直角在坐标系中，四边形OACB的两边OA，OB分别在x轴、y轴的正半轴上，其中，且CO平分，若，，则点C的坐标为______．

12．如图，在平面直角坐标系中，点A（0，4）在y轴正半轴上，点B（－3，0）在x轴负半轴上，且AB=5，点M坐标为（3，0），N点为线段OA上一动点，P为线段AB上的一动点，则MN+NP的最小值为___________．

13．如图，平面直角坐标系中，A（﹣3，0）B（0，4）把△AOB按如图标记的方式连续做旋转变换，这样得到的第2017个三角形中，O点的对应点的坐标为_____．

14．如图，在平面直角坐标系中，点、点，点P是x轴正半轴上—动点，给出4个结论：
①线段AB的长为；
②在，若，则的面积是5；
③当时，点P的坐标为；
④设点P的坐标为，则的最小值为．
其中正确的结论有______．

15．如图，在平面直角坐标系中，点，点，将线段绕着点P逆时针旋转90°，得到线段，连接，，则的最小值为__________．

16．如图，在平面直角坐标系中，点，点是x轴上的一个动点．

（1）用含x的式子表示线段的长是_____；
（2）结合图形，判断式子的最小值是____．
17．如图，等腰是由三块面向内的镜面组成的，其中，边上靠近点的三等分点处发出一道光线，经镜面两次反射后恰好回到点，若，则光线走过的路径是______．

18．如图，点的坐标为，点的坐标为，分别以，为直角边在第三、第四象限作等腰，等腰，连接交轴于点，点的坐标是______．

19．如图，在平面直角坐标系中，是边长为的等边三角形，是边上的高，点是上的一个动点，若点的坐标是，则的最小值是________．

20．在平面直角坐标系中，点A（3，0），B（0，6），作△BOC，使△BOC与△ABO全等，则点C坐标为 _______________．
三、解答题
21．在平面直角坐标系中，点A的坐标为，过点作x轴的垂线l，点A与点B关于直线l对称；
(1) 点B的坐标为________；
(2) 点C的坐标为，顺次连接，若在四边形内部有一个点P，满足，且，求点P的坐标；
(3) 在四边形外部是否存在点Q，满足，且，若存在，直接写出Q点坐标，若不存在请说明理由．


22．如图，的顶点A，B分别在x轴，y轴上，；
(1) 若，且点B（0，2），C（-2，-1），
① 点C关于y轴对称点的坐标为______；
② 求点A的坐标；
(2) 若点B与原点重合，时，存在第三象限的点E和y轴上的点F，使，且A（3，0），C（0，m），F（0，n），线段EF的长度为，求AE的长．


23．对于平面内的及其内部的一点，设点到直线，的距离分别为，，称和这两个数中较大的一个为点关于的“偏率”在平面直角坐标系中，点，分别为轴正半轴，轴正半轴上的两个点．
(1) 若点的坐标为，则点关于的“偏率”为______；
(2) 若第一象限内点关于的“偏率”为1，则，满足的关系为______；
(3) 若第一象限内点关于的“偏率”为2．在平面直角坐标系上，画出所有点E形成的图形．




24．如图，在平面直角坐标系中，已知，，其中，满足，点为第三象限内一点.
（1）若到坐标轴的距离相等，，且，求点坐标
（2）若为，请用含的式子表示的面积.
（3）在（2）条件下，当时，在轴上有点，使得的面积是的面积的2倍，请求出点的坐标.



25．已知：在平面直角坐标系中，点在第四象限，且到x轴的距离为2，到y轴的距离为1．
(1) 求点的坐标；
(2) 若轴，且点C到x轴的距离与点A到x轴的距离相等，请直接写出点C的坐标；
(3) 在坐标轴上是否存在一点M，使的面积的面积的一半？若存在，请求出点M的坐标；若不存在，请说明理由．
26．如图，在平面直角坐标系中，点A、B的坐标分别为、，且实数a、b满足．

(1) 求A、B两点的坐标；
(2) 如图1，已知坐标轴上有两动点P，Q同时出发，P点从A点出发沿x轴负方向以每秒2个单位长度的速度向点O匀速移动，Q点从O点出发沿y轴正方向以每秒1个单位长度的速度向点B匀速移动，点P到达O点整个运动随之结束．AB的中点C的坐标是，设运动时间为t秒．是否存在这样的t，使得的面积等于面积的2倍？若存在，请求出t的值；若不存在，请说明理由；
(3) 如图2，在（2）的条件下，若，点G是第二象限中一点，并且y轴平分．点E是线段OB上一动点，连接AE交OC于点H，当点E在线段OB上运动的过程中，探究，，之间的数量关系，并证明你的结论（三角形的内角和为180°可以直接使用）．






















参考答案
1．C
【分析】
根据f，g两种变换的定义自内而外进行解答即可．
解：由题意得，f（5，﹣9）]＝（﹣5，﹣9），
∴g[f（5，﹣9）]＝g（﹣5，﹣9）＝（﹣9，﹣5），
故选：C．
【点拨】本题考查了新定义坐标变换，根据题意、弄懂两种变换的方法是解答本题的关键．
2．D
【分析】
据“伴随点”的定义依次求出各点，不难发现，每4个点为一个循环组依次循环，用2021除以4，根据商和余数的情况确定点的坐标即可．
解：观察发现：，，，，，
依此类推，每4个点为一个循环组依次循环，
余1，
点的坐标与的坐标相同，为，
故选：D．
【点拨】本题是对点的变化规律的考查，读懂题目信息，理解“伴随点”的定义并求出每4个点为一个循环组依次循环是解题的关键．
3．B
【分析】
根据第二象限的点的特点可知，即可得，，计算可得；a，b均为整数，所以或；据此分别可求出A点的坐标，即可得本题答案．
解：∵点位于第二象限，
∴，
∴，，
∴
∴，
∵a，b均为整数，
∴或，
当时，，；
当时，，或或或；
综上所述，满足条件的点A个数有5个．
故选：B．
【点拨】本题主要考查第二象限点的坐标特点及解不等式的知识；熟练掌握个象限点坐标的符号特点，是解决本题的关键．
4．B
【分析】
根据题意可得前6个点的坐标，即可发现规律每6个点一组为一个循环，根据2020÷6=336…4，进而可得点P2020的坐标．
解：∵A（1，﹣1），B（﹣1，﹣1），C（0，1），
点P（0，2）关于点A的对称点P1，
∴，，
解得x＝2，y＝﹣4，
所以点P1（2，﹣4）；
同理：
P1关于点B的对称点P2，
所以P2（﹣4，2）
P2关于点C的对称点P3，
所以P3（4，0），
P4（﹣2，﹣2），
P5（0，0），
P6（0，2），
…，
发现规律：
每6个点一组为一个循环，
∴2020÷6＝336…4，
所以点P2020的坐标是（﹣2，﹣2）．
故选：B．
【点拨】本题考查了坐标与图形的变化-旋转、规律型-点的坐标、关于x轴、y轴对称的点的坐标，解决本题的关键是掌握旋转的性质．
5．B
【分析】
过点C作CD⊥x轴于D，由“AAS”可证△AOB≌△BDC，可得AO＝BD＝2，BO＝CD＝n＝a，即可求解．
解：如图，过点C作CD⊥x轴于D，

∵点A（0，2），
∴AO＝2，
∵△ABC是等腰直角三角形，且AB＝BC，
∴∠ABC＝90°＝∠AOB＝∠BDC，
∴∠ABO+∠CBD＝90°
∠ABO+∠BAO＝90°，
∴∠BAO＝∠CBD，
在△AOB和△BDC中，
，
∴△AOB≌△BDC（AAS），
∴AO＝BD＝2，BO＝CD＝n＝a，
∴0＜a＜1，
∵OD＝OB+BD＝2+a＝m，
∴2＜m＜3，
故选：B．
【点拨】本题考查了等腰直角三角形的性质、全等三角形的性质与判定、不等式和坐标等知识，解题关键是树立数形结合思想，把坐标与线段长联系起来，确定取值范围．
6．D
【分析】
首先证明AB=AC=a，根据条件可知PA=AB=AC=a，求出⊙D上到点A的最大距离即可解决问题．
解：∵A（1，0），B（1-a，0），C（1+a，0）（a＞0），
∴AB=1-（1-a）=a，CA=a+1-1=a，
∴AB=AC，
∵∠BPC=90°，
∴PA=AB=AC=a，
如图延长AD交⊙D于P′，此时AP′最大，

∵A（1，0），D（4，4），
∴AD=5，
∴AP′=5+1=6，
∴a的最大值为6．
故选D．
【点拨】本题考查圆、最值问题、直角三角形性质等知识，解题的关键是发现PA=AB=AC=a，求出点P到点A的最大距离即可解决问题，属于中考常考题型．
7．B
【分析】
根据含角的直角三角形的性质，结合图形即可得到规律，依此规律即可解决问题．
解：∵∠AOB=30°，点A坐标为(2，0)，
∴OA=2，
∴OA1=OA=，OA2=OA1=2×，OA3=OA2=2×……，
∴OAn=()nOA=2()n．
∴OA2018=2×()2018=•()2016
故选：B
【点拨】此题着重培养学生的观察、实验和猜想、归纳能力，掌握从特殊到一般的猜想方法．
8．C
解：M点与A点关于原点对称，A点与N点关于x轴对称，由平面直角坐标中对称点的规律知：M点与A点的横、纵坐标都互为相反数，N点与A点的横坐标相同，纵坐标互为相反数．所以M（－1，－3），N（1，－3）．
9．C
【分析】
根据题意作出平面直角坐标系，根据图象可以直接得到答案．
解：∵点A的坐标为，点B的坐标为，
如图，依题意可画出直角坐标系，

∴点A位于第四象限，点B位于第二象限，
∴点C位于第三象限．
故选：C．
【点拨】考查了坐标与图形性质，解题时，利用了“数形结合”的数学思想，比较直观，应用“数形结合”的数学思想是解题的关键．
10．C
分析：如图，作AH、CK、FP分别垂直BC、AB、DE于H、K、P．由AB=BC，△ABC≌△DEF，就可以得出△AKC≌△CHA≌△DPF，就可以得出结论．
解：如图，作AH、CK、FP分别垂直BC、AB、DE于H、K、P，∴∠DPF=∠AKC=∠CHA=90°．
∵AB=BC，∴∠BAC=∠BCA．
在△AKC和△CHA中，
∵，∴△AKC≌△CHA（ASA），∴KC=HA．
 ∵B、C两点在方程式y=﹣3的图形上，且A点的坐标为（﹣3，1），∴AH=4，∴KC=4．
 ∵△ABC≌△DEF，∴∠BAC=∠EDF，AC=DF．
在△AKC和△DPF中，，∴△AKC≌△DPF（AAS），∴KC=PF=4．
故选C．
       
【点拨】本题考查了坐标与图象的性质的运用，垂直的性质的运用，全等三角形的判定及性质的运用，等腰三角形的性质的运用，解答时证明三角形全等是关键．
11．
【分析】
取AB的中点E，连接OE，CE并延长交x轴于点F，根据直角三角形斜边 上的中线等于斜边的一半证明CE=OE=AE，再进一步证明；由勾股定理求出AB=，AO=BO=5；过点O作OG⊥OC交CA的延长线于点G，证明△COG访问团等腰直角三角形，可可求出OC=7；过点C作CH⊥x轴，垂足为H，设C（m，n），则OH=m，CH=n，AH=5-m，根据勾股定理可得方程组 ，求出方程组的解，取正值即可．
解：取AB的中点E，连接OE，CE并延长交x轴于点F，如图，

∵，OC平分∠ACB，
∴
∵均为直角三角形，
∴
∴
∴
∴
∵
∴
∴
∴
∴是等腰直角三角形，
∴
∵
由勾股定理得，
∴
∴
过点O作OE⊥OC交CA的延长线于点G，
∵∠OCA=45°，
∴∠G=45°，
∴△COG为等腰直角三角形，
∴OC=OG，
∵∠BOC+∠COA=∠COA+∠AOG=90°，
∴∠BOC=∠AOG，
∵∠OCB=∠OEA=45°，
∴△COB≌△GOA（ASA），
∴BC=AG=，
∵CG=AC+AG=
∵△OCE为等腰直角三角形，
∴OC=7
过点C作CH⊥x轴于点H，设C（m，n），
∴OH=m，CH=n，AH=5-m
在Rt△CHO和Rt△CHA中，由勾股定理得，

解得，，（负值舍去）
∴C（）
故答案为：（）
【点拨】本题主要考查了坐标玮图形的性质，全等三角形的判定和性质，等腰直角三角形的性质，勾股定理，添加恰当辅助线构造全等三角形是本题的关键．
12．
【分析】
连接AM，根据点A（0，4），点B（-3，0），点M坐标为（3，0），得到OA=4，OB=3，OM=3，过M作MP⊥AB于P交OA于N，则此时，MN+NP的值最小，且MN+NP的最小值=MP，根据三角形的面积公式即可得到结论．
解：连接AM，
∵点A（0，4），点B（-3，0），点M坐标为（3，0），
∴OA=4，OB=3，OM=3，
过M作MP⊥AB于P交OA于N，
则此时，MN+NP的值最小，且MN+NP的最小值=MP，
∵， BM=6，OA=4，AB=5，
∴．
故答案为：．

【点拨】本题考查垂线段最短的应用，坐标与图形性质，三角形的面积公式，正确的作出图形是解题的关键．
13．（8064，0）
解：∵A（﹣3，0），B（0，4），∴OA=3，OB=4，由勾股定理得：AB===5，∴△ABC的周长=3+4+5=12．∵△OAB每连续变换3次后与原来的状态一样，2017÷3=672…1，∴第2017个三角形的直角顶点是第673个循环组第一个三角形的直角顶点，∴三角形2017的直角顶点O的横坐标=672×12=8064，∴三角形2017的直角顶点O的坐标为（8064，0）．故答案为（8064，0）．
【点拨】本题考查了坐标与图形变化﹣旋转，仔细观察图形得到每三个三角形为一个循环组依次循环是解题的关键，也是求解的难点．
14．①②④
【分析】
①直接利用根据两点间距离的坐标公式计算AB的长度即可；②先证明为直角三角形，然后根据三角形面积的公式直接计算面积即可；③先求出△ABO和△ABP的面积，然后过点B作轴于点D，继而求出梯形AOBD的面积，设点P的坐标，最后根据求出点P的坐标即可；④作A点关于x轴的对称点M，设出点P的坐标，继而表示出AP、MP和BP的长度，可以得到，当且仅当B，P，M三点共线时，代数式取得最小值；
解：①根据两点间距离的坐标公式可知，，故①正确；
②在中，，，，
∴(1，0)，
∴，
在中，，
∴为直角三角形，
∴，故②正确.
∵，
∴，
过点B作轴于点D，即，，

∴

，
设P点坐标为(m，0)，
∴，
，
∴，
∴，
∴，
解得，
∴当时，点P的坐标为(3，0)，故③错误.
作A点关于x轴的对称点M，
连接BM交x轴于点P，

此时，
∵P点坐标为(x，0)，
∴，
，
∴
，
当且仅当B，P，M三点共线时，
代数式取得最小值，
最小值即为线段BM的长度，
∵(0，-3)，B(4，1)
∴，
∴的最小值为.
故④正确.
∴正确的有①②④.
故答案为：①②④.
【点拨】本题考查了图形与坐标的特点，直角三角形的判定，三角形的面积公式，两点之间距离公式，求最值的问题，是一个考点比较全面的综合题，难度适中，熟练掌握知识点的应用是解题的关键；
15．
【分析】
过点B作BC⊥y轴于点C，作O关于直线BC的对称点D，连接AD，BD，由题意易得△BCP≌△POA，则有PC=OA=6，BC=OP=m，则有CO=6+m，DO=12+2m，由三角不等关系可知，进而问题可求解．
解：过点B作BC⊥y轴于点C，作O关于直线BC的对称点D，连接AD，BD，如图所示：

∵，
∴，
∵，
∴，
∵，
∴△BCP≌△POA，
∵点，点，
∴PC=OA=6，BC=OP=m，
∴CO=6+m，
由轴对称可知：，
∴DO=12+2m，
由三角不等关系可知，即，
∴AB+OB的最小值即为AD的长，
∴
∴当m=0时，AD最短，为；
故答案为．
【点拨】本题主要考查图形与坐标、勾股定理、轴对称的性质及全等三角形的判定与性质，熟练掌握图形与坐标、勾股定理、轴对称的性质及全等三角形的判定与性质是解题的关键．
16．          5
【分析】
（1）直接根据坐标系中两点之间的距离公式计算即可；
（2）根据题意得出求PA+PB的最小值，作点B关于x轴的对称点B’，连接AB’与x轴交于点P’，此时PA+PB取得最小值，利用坐标系中两点之间的距离公式求解即可得出结果．
解：（1），
故答案为：；
（2）由题意可得：，即为求PA+PB的最小值，
作点B关于x轴的对称点B’，连接AB’与x轴交于点P’，此时PA+PB取得最小值，如图所示：

PA+PB=AB’=，
即的最小值为5，
故答案为：5．
【点拨】题目主要考查距离最短问题、坐标系中两点之间的距离及轴对称的性质等，理解题意，作出相应图形求解是解题关键．
17．
【分析】
根据题意，建立直角坐标系，写出对应点坐标，利用光的反射原理与对称性，求出点、的坐标，勾股定理即可求解．
解：建立如图所示的直角坐标系，，分别是点关于直线和轴的对称点，连接AM，

，D为边上靠近点的三等分点，
可得，，，，，
，
设，分别是点关于直线和轴的对称点，
则，，
由光的反射原理可知，、、、四点共线，，，
光线走过的路径，
，
即光线走过的路径是．
故答案为：．
【点拨】本题考查三角形的性质与轴对称图形的灵活应用问题，关键在于正确建立直角坐标系并求解．
18．
【分析】
作轴于，求出，证，得BN=AO，再由，证，推出=2，由点的坐标为即可得出点的坐标为．
解：如图，作轴于，

，
，，
，
在和中，

，
，OA=BN
，
在和中，
，
，
，
又因为点的坐标为，
，
，
又∵点的坐标为，
∴点的坐标为．
故答案为：．
【点拨】本题考查了全等三角形的性质和判定，坐标与图形性质等知识点的应用，主要考查学生综合运用性质进行推理和计算的能力，有一定的难度，注意：全等三角形的判定定理有，，，，全等三角形的对应角相等，对应边相等．
19．
【分析】
过B作BE⊥y轴于E，连接BP，依据OD垂直平分AB，可得AP＝BP，PA+PC＝BP+PC，当C，P，B三点共线时，PA+PC的最小值等于BC的长，在Rt△BCE中利用勾股定理即可得到BC的长，进而得出PA+PC的最小值是．
解：如图，

过B作BE⊥y轴于E，连接BP，
∵△OAB是边长为的等边三角形，OD是AB边上的高，
∴OD是中线，
∴OD垂直平分AB，
∴AP＝BP，
∴PA+PC＝BP+PC，
当C，P，B三点共线时，PA+PC的最小值等于BC的长，
∵ ，OB＝，
∴BE＝，OE＝3，
又∵点C的坐标是（0，），
∴OC＝，CE＝4，
∴Rt△BCE中，BC＝＝＝，
即PA+PC的最小值是，
故答案为： ．
【点拨】本题考查了轴对称确定最短路线问题，熟练掌握最短路径的确定方法找出点P的位置以及表示PA+PC的最小值的线段是解题的关键．凡是涉及最短距离的问题，一般要考虑线段的性质定理，结合轴对称变换来解决，多数情况要作点关于某直线的对称点．
20．或或
【分析】
根据直角坐标系的性质，得，，；再根据全等三角形性质，分三种情况分析，即可得到答案．
解：根据题意，得，，
使△BOC与△ABO全等，分三种情况分析：
当时，如下图

∵△BOC与△ABO全等，且
∴
∴
当时，如下图

∵△BOC与△ABO全等，且
∴
∴
当时，如下图

∵△BOC与△ABO全等，且
∴
∴
故答案为：或或．
【点拨】本题考查了直角坐标系、全等三角形的知识；解题的关键是熟练掌握直角坐标系、坐标、全等三角形的性质，从而完成求解．
21．(1)(2)(3)存在，
【分析】
（1）根据对称性可知到的距离相等，且纵坐标相等，据此即可求解；
（2）根据对称性可知点与点关于对称，则点在上，设点，根据三角形的面积公式求解即可求解；
（3）方法同（2）即可求解．
解：(1)点A的坐标为，过点作x轴的垂线l，
到的距离为,
则
故答案为：
(2)如图，,，
点与点关于对称，
在四边形内部有一个点P，满足，
则点在上，设点，
，




即
解得或
在四边形内部



(3)存在，由（2）可知时，在四边形外部
故
【点拨】本题考查了坐标与图形，轴对称的性质，点到坐标轴的距离，数形结合是解题的关键．
22．(1)①（2，-1）；②（3,0）．(2)6．
【分析】
（1）①根据关于y轴对称的点纵坐标不变、横坐标变为原来的相反数即可解答；②设A点坐标为（a，0），再运用两点间距离公式求得BC的长，进而求得AB的长，然后根据两点间距离公式即可求解；
（2）作点F关于x轴的对称点H（0，-n），则AF=AH、OF=OH，过点H作HN⊥AC于点N，过点F作FM⊥AE于点M，则C（0，m）、H（0，-n）、m<0、n>0，进一步说明HC=EF；然后再证明△FEM≌△HCN得到FM=HN、EM=CN，证明Rt△AFM≌Rt△AHN得到AM=AN，进一步说明AE=AC，最后求得AC的长即可．
(1)解：（1）①由关于y轴对称的点纵坐标不变、横坐标变为原来的相反数，则点C（-2，-1）关于y轴对称点的坐标为（2，-1）；
故答案是（2，-1）；
②设A点坐标为（a，0）
∵B（0，2），C（-2，-1），
∴BC=
∴AB=BC=
∴，解得a=3.
∴点A的坐标为（3,0）．
(2)解：（2）作点F关于x轴的对称点H（0，-n），则AF=AH、OF=OH，过点H作HN⊥AC于点N，过点F作FM⊥AE于点M，
∵C（0，m），H（0，-n），m<0，n>0，
∴HC=OC-OH=-m-n，
∵EF=-m-n，
∴HC=EF，
∵∠AEF=∠ACO=30°，
∴∠FME=∠HNC，
∴△FEM≌△HCN（AAS），
∴FM=HN，EM=CN，
在Rt△AFM和Rt△AHN中，
AF=AH，FM=HN
∴Rt△AFM≌Rt△AHN（HL），
∴AM=AN，
∴EM+AM=CN+AN，
∴AE=AC，
∵∠ACO=30°，A（3，0），
∴OA=3，
∴AC=2OA=6，
∴AE=6．

【点拨】本题主要考查了轴对称、两点间的距离公式、勾股定理、全等三角形的判定与性质等知识点，综合应用相关知识成为解答本题的关键．
23．(1)5(2)a＝b(3)见分析
【分析】
（1）根据“偏率”的定义，求点P到OM（即x轴）的距离和点P到ON（即y轴）的距离，用较大的数除以较小的数即为“偏率”；
（2）根据“偏率”定义，可知点Q到OM、ON距离相等，且Q在第一象限，所以其横纵坐标相等；
（3）根据“偏率”定义，可知点E到OM、ON距离之比为2，且E在第一象限，所以其图像如图所示．
(1)解：∵点M，N分别在x轴正半轴，y轴正半轴上，
∴点P（1，5）到OM距离d1＝5，到ON距离d2＝1，
∴点P关于∠MON的“偏率”为：5；
故答案为：5；
(2)∵点Q（a，b）在第一象限，到OM距离d1＝b，到ON距离d2＝a，
∴点Q关于∠MON的“偏率”为：1或1，
∴a＝b，
故答案为：a＝b；
(3)∵点在第一象限，
∴点E到OM距离d1＝y，到ON距离d2＝x，
又∵点E关于的“偏率”为2，
∴点E关于∠MON的“偏率”为：2或，
即点E在函数或的图象上，
点E形成的图形如图所示：

【点拨】本题考查了新定义的理解，点到直线距离，平面直角坐标系点的特征，解题关键是新定义的理解和应用，根据新定义的表述画出图形数形结合地解决问题．
24．（1）或；（2）；（3）或.
【分析】
（1）利用M在第三象限且到坐标轴的距离相等，求出M点坐标，同时利用绝对值与算术平方根的非负性求出a、b，得到AB的长度，再利用，求出N点
（2）利用三角形的面积公式直接写出即可，注意m的取值范围
（3）同（2）利用面积公式写出两个三角形的面积，然后列出方程解方程
解：（1）由题意可知:

，
求得，
∵，
∴，，
∴，，
∴，
∵，，
∴，
∵，
∴或者，
∴或；
（2）由题意可得：
，
∵在三象限，
∴，
∴；
（3）当时，，
由题意可得：
，
，
，
，
∴或.
【点拨】本题主要考查坐标与图形性质，涉及到非负数的性质，三角形的面积等知识点，第二问和第三问要重点注意是有两种情况的.
25．(1)；(2)；(3)y轴上不存在，x轴上，．
【分析】
（1）根据点A到坐标轴的距离可求出a、b的值，代入即可求出B点坐标；
（2）由（1）可知：，利用轴，点C到x轴的距离与点A到x轴的距离相等，可得C的横坐标为1，纵坐标为2，即可求出点C坐标；
（3）当点M在y轴上时，设，则，所以点M不能在y轴上，设，到AC的距离为h，根据，可得，，进一步可求出M坐标．
(1)解：∵点在第四象限，且到x轴的距离为2，到y轴的距离为1，
∴，解得：，
∴，，
∴
(2)解：由（1）可知：，
∵轴，点C到x轴的距离与点A到x轴的距离相等，
∴C的横坐标为1，纵坐标为2，
∴
(3)解：假设存在点M，使得，
∵，，
∴，
∴，
当点M在y轴上时，设，则，
∴点M不能在y轴上，
设，到AC的距离为h，如图：

则，，
当M位于AC左侧时，，得；
当M位于AC右侧时，，得；
综上所述：，．
【点拨】本题考查直角坐标系，解题的关键是掌握点到坐标轴的距离，点所在象限的特征，当轴时，点的坐标特点，三角形面积公式，坐标轴上两点间的距离．
26．(1)A（16，0），B（0，12）(2)存在，(3)2∠GOB+∠BAE=∠OHA，理由见分析
【分析】
（1）根据算术平方根的非负性列出二元一次方程组，解方程组得到答案；
（2）根据题意用t表示出OP、OQ，根据三角形的面积公式列出方程，解方程即可求出t；
（3）过点H作HF∥OG交x轴于F，根据平行线的性质得到∠OHF=∠GOH，证明HF∥AB，根据平行线的性质得到∠AHF=∠BAE，结合图形计算，证明结论．
（1）解：∵，∴，解得：，∴A（16，0），B（0，12）；
（2）解：存在t，使得△OCP的面积等于△OCQ面积的2倍由（1）知，A（16，0），B（0，12），∴OA=16，OB=12，∵，∴，∵C（8，6），∴，，∵△OCP的面积等于△OCQ面积的2倍，∴ ，解得：，∴当时，△OCP的面积等于△OCQ面积的2倍；
（3）解：2∠GOB+∠BAE=∠OHA，理由如下：∵∠COA+∠BOC=∠BOA=90°，∴∠OBA+∠BAO=90°，又∵∠COA=∠CAO，∴∠OBA=∠BOC，∵y轴平分∠GOC，∴∠GOB=∠BOC，∴∠GOB=∠OBA，∴OG∥BA，过点H作HF∥OG交x轴于F，
∴HF∥BA，∴∠FHA=∠BAE，∵OG∥FH，∴∠GOC=∠FHO，∴∠GOC+∠BAE=∠FHO+∠FHA，即∠GOC+∠BAE=∠OHA，∴2∠GOB+∠BAE=∠OHA．
【点拨】本题考查的是非负性的性质，三角形的面积公式，角平分线的定义，平行线的性质，正确作出辅助线是解本题的关键．