广西梧州市岑溪市3年（2020-2022）八年级数学上学期期末试题汇编-01选择题

广西梧州市岑溪市3年（2020-2022）八年级数学上学期期末试题汇编-01选择题

1．（2022·广西梧州·八年级期末）三角形的内角和等于（    ）

A． B． C． D．

2．（2022·广西梧州·八年级期末）当时，函数的值等于（    ）

A． B． C． D．

3．（2022·广西梧州·八年级期末）在平面直角坐标系中，把点向左平移1个单位后所得的点的坐标是（    ）

A． B． C． D．

4．（2022·广西梧州·八年级期末）下列四个图案分别是四届国际数学家大会的会标，其中是轴对称图形的共有（    ）

A．1个 B．2个 C．3个 D．4个

5．（2022·广西梧州·八年级期末）下列给出的简记中，不能判定两个三角形全等的是（    ）

A． B． C． D．

6．（2022·广西梧州·八年级期末）已知一次函数的图象经过点，则k的值是（    ）

A．1 B．0 C． D．4

7．（2022·广西梧州·八年级期末）已知一个三角形有两边长分别为3和9，则它的第三边长可能是（    ）

A．4 B．5 C．6 D．7

8．（2022·广西梧州·八年级期末）到三角形三条边距离相等的点是此三角形（　　）

A．三条角平分线的交点 B．三条中线的交点

C．三条高的交点 D．三边中垂线的交点

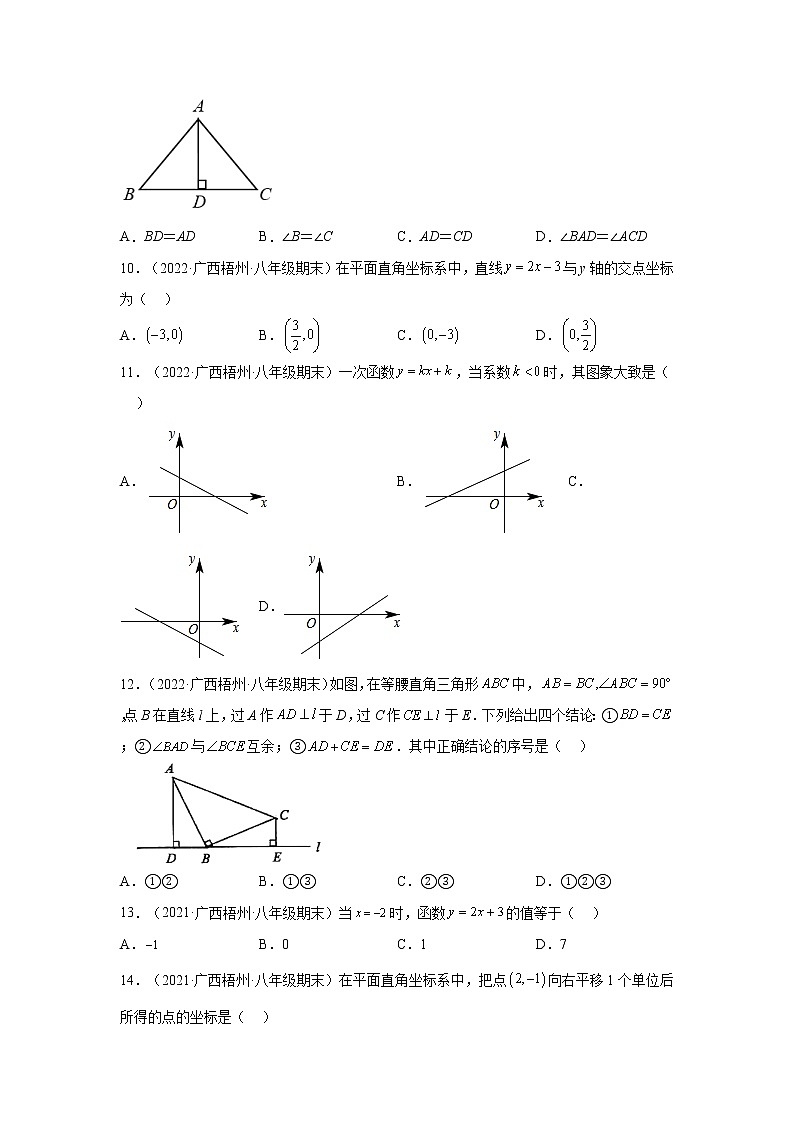
9．（2022·广西梧州·八年级期末）如图，在ABC中，AB＝AC，AD⊥BC于点D，则下列结论，一定成立的是（    ）

A．BD＝AD B．∠B＝∠C C．AD＝CD D．∠BAD＝∠ACD

10．（2022·广西梧州·八年级期末）在平面直角坐标系中，直线与y轴的交点坐标为（    ）

A． B． C． D．

11．（2022·广西梧州·八年级期末）一次函数，当系数时，其图象大致是（    ）

A． B． C． D．

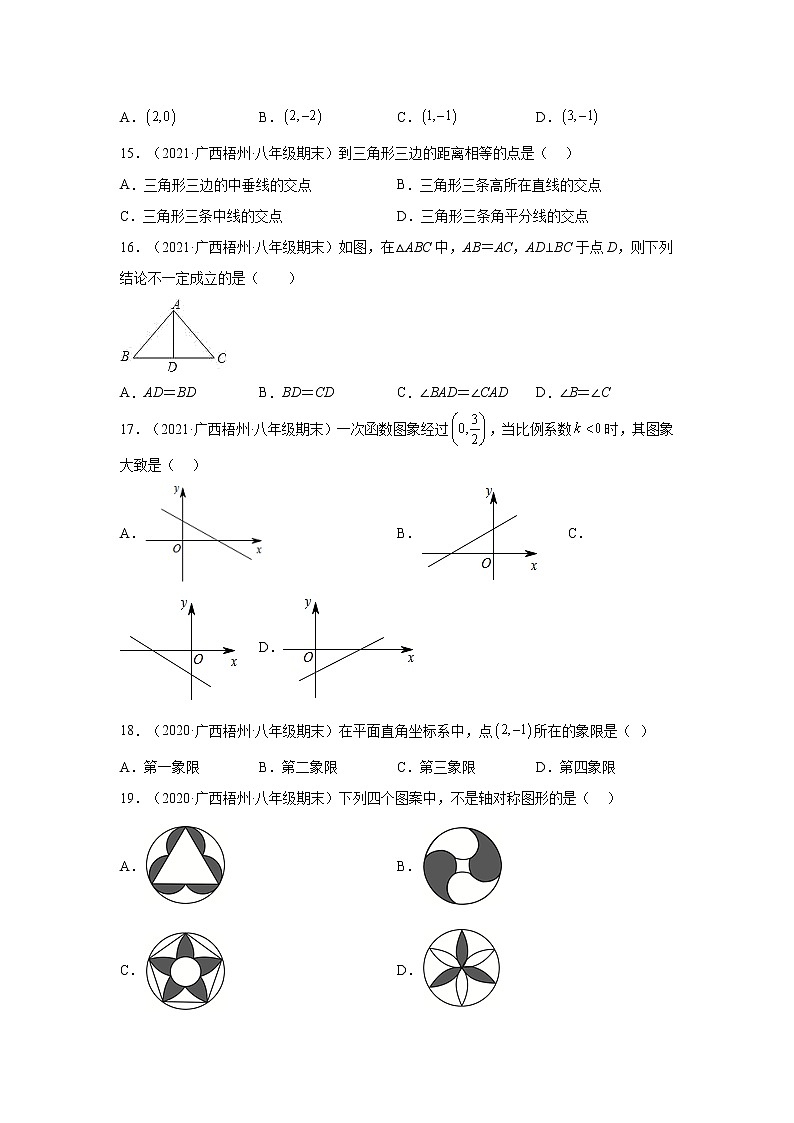
12．（2022·广西梧州·八年级期末）如图，在等腰直角三角形中，，点B在直线l上，过A作于D，过C作于E．下列给出四个结论：①；②与互余；③．其中正确结论的序号是（    ）

A．①② B．①③ C．②③ D．①②③

13．（2021·广西梧州·八年级期末）当时，函数的值等于（    ）

A． B．0 C．1 D．7

14．（2021·广西梧州·八年级期末）在平面直角坐标系中，把点向右平移1个单位后所得的点的坐标是（    ）

A． B． C． D．

15．（2021·广西梧州·八年级期末）到三角形三边的距离相等的点是（    ）

A．三角形三边的中垂线的交点 B．三角形三条高所在直线的交点

C．三角形三条中线的交点 D．三角形三条角平分线的交点

16．（2021·广西梧州·八年级期末）如图，在△ABC中，AB＝AC，AD⊥BC于点D，则下列结论不一定成立的是（　　）

A．AD＝BD B．BD＝CD C．∠BAD＝∠CAD D．∠B＝∠C

17．（2021·广西梧州·八年级期末）一次函数图象经过，当比例系数时，其图象大致是（    ）

A． B． C． D．

18．（2020·广西梧州·八年级期末）在平面直角坐标系中，点所在的象限是（  ）

A．第一象限 B．第二象限 C．第三象限 D．第四象限

19．（2020·广西梧州·八年级期末）下列四个图案中，不是轴对称图形的是（    ）

A． B．

C． D．

20．（2020·广西梧州·八年级期末）以下列长度的线段为边，可以作一个三角形的是（  ）

A． B． C． D．

21．（2020·广西梧州·八年级期末）点到轴的距离是（  ）

A． B． C． D．

22．（2020·广西梧州·八年级期末）如图，线段与相交于点，连接，且，要使，应添加一个条件，不能证明的是（  ）

A． B． C． D．

23．（2020·广西梧州·八年级期末）在下列命题中，真命题是（  ）

A．相等的角是对顶角 B．同位角相等

C．三角形的外角和是 D．角平分线上的点到角的两边相等

24．（2020·广西梧州·八年级期末）如图，是岑溪市几个地方的大致位置的示意图，如果用表示孔庙的位置，用表示东山公园的位置，那么体育场的位置可表示为（  ）

A． B． C． D．

25．（2020·广西梧州·八年级期末）在建筑工地我们常可看见如图所示，用木条EF固定矩形门框ABCD的情形．这种做法根据（　　）

A．两点之间线段最短 B．两点确定一条直线 C．三角形的稳定性 D．矩形的四个角都是直角

26．（2020·广西梧州·八年级期末）一次函数y＝﹣3x﹣2的图象和性质，表述正确的是（　　）

A．y随x的增大而增大 B．在y轴上的截距为2

C．与x轴交于点（﹣2，0） D．函数图象不经过第一象限

27．（2020·广西梧州·八年级期末）如图，一次函数y1＝x＋b与一次函数y2＝kx＋4的图象交于点P（1，3），则关于x的不等式x＋b＞kx＋4的解集是（　　）

A．x＞﹣2 B．x＞0 C．x＞1 D．x＜1

28．（2020·广西梧州·八年级期末）如图，在中，平分于.如果，那么等于（  ）

A． B． C． D．

29．（2020·广西梧州·八年级期末）如图，△ABC中，∠ABC＝45°，CD⊥AB于D，BE平分∠ABC，且BE⊥AC于E，与CD相交于点F，DH⊥BC于H，交BE于G，下列结论：①BD＝CD；②AD+CF＝BD；③CE＝BF；④AE＝BG．其中正确的是（　　）

A．①② B．①③ C．①②③ D．①②③④

【答案】

1．C

【分析】根据三角形内角和定理即可判断．

【详解】解：∵三角形的内角和等于180°，

故选：C．

【点睛】本题考查了三角形内角和定理，解题关键是熟记三角形内角和定理．

2．A

【分析】把代入解析式即可．

【详解】解：把代入得，

，

故选：A．

【点睛】本题考查了求一次函数的函数值，解题关键是把自变量的值代入后能准确熟练计算．

3．C

【分析】根据点坐标平移的性质，把点横坐标减一，纵坐标保持不变即可求解．

【详解】解：把点向左平移1个单位，即横坐标减一，纵坐标保持不变，故把点向左平移1个单位后所得的点的坐标是．

故选：C．

【点睛】此题考查了点坐标的平移问题，解题的关键是点坐标平移的性质．

4．B

【分析】根据轴对称图形的性质判断即可．

【详解】解：观察图片可知，第二个图片和第四个图片是轴对称图形，

故选：B．

【点睛】本题考查了轴对称图形的识别，解题关键是抓住轴对称图形的特征，仔细认真判断．

5．B

【分析】根据全等三角形的判定定理，即可得到答案．

【详解】，，能判定两个三角形全等，不能判定两个三角形全等，

故选B．

【点睛】本题主要考查全等三角形的判定定理，熟练掌握“SSS，SAS，AAS，ASA，HL”是解题的关键．

6．A

【分析】把点（5，2）代入一次函数y=kx﹣3即可解出k的值.

【详解】把点（5，2）代入一次函数y=kx﹣3

得2=k×5-3，

解得k=1，

故选：A.

【点睛】此题主要考查了一次函数的性质，代入求值即可解题.

7．D

【分析】根据三角形的三边关系“第三边大于两边之差，而小于两边之和”，求得第三边的取值范围．

【详解】解：根据三角形的三边关系，设第三边的长为x，

∵三角形两边的长分别是3和9，

∴9-3＜x＜9+3，

即6＜x＜12．

则它的第三边长可能是7

故选：D．

【点睛】此题考查了三角形的三边关系，关键是正确确定第三边的取值范围．

8．A

【分析】根据角平分线的性质进行解答即可．

【详解】解：角平分线上任意一点，到角两边的距离相等，

到三角形三条边距离相等的点是三角形三个内角的平分线的交点，

故选：A．

【点睛】本题考查的是角平分线的性质，熟知角平分线上任意一点，到角两边的距离相等是解答此题的关键．

9．B

【分析】根据直角三角形全等的特殊判定方法（直角边斜边）得出，再由全等三角形的性质依次判断各选项即可得．

【详解】解：∵，

∴，

在与中，

，

∴，

∴，，，

故选：B．

【点睛】题目主要考查直角三角形全等的判定定理和性质，熟练掌握全等三角形的判定定理是解题关键．

10．C

【分析】令中x=0即可求解．

【详解】解：由题意可知：令中x=0，

即，

∴直线与y轴的交点坐标为，

故选择：C．

【点睛】本题考查了一次函数图象上点的坐标特征，掌握一次函数图象上点的坐标特征，和坐标轴上点的特征，与x轴的交点则令解析式中y=0，与y轴的交点则令解析式中x=0即可求解．

11．C

【分析】根据一次函数图象的性质解答即可．

【详解】解：∵，

∴y随x的增大而减小，且图象与y轴的负半轴相交，

∴图象经过二三四象限，

故选C．

【点睛】本题考查了一次函数的图象与性质，对于一次函数y=kx+b（k为常数，k≠0）当k>0，y的值随x的值增大而增大；当k＜0，的值随x的值增大而减小．

12．D

【分析】证△ADB≌△BEC即可．

【详解】证明：∵， ，

∴∠ADB=∠BEC=90°，

∴∠BAD+∠ABD=90°，∠BCE+∠CBE=90°，

∵，

∴∠ABD+∠CBE=90°，

∴∠BAD=∠CBE，

∴∠BCE+∠BAD=90°，故②正确；

∵∠BAD=∠CBE，∠ADB=∠BEC=90°，

∴△ADB≌△BEC，

∴，AD=BE，故①正确；

DE=DB+BE=CE+AD，故③正确；

故选：D．

【点睛】本题考查了全等三角形的判定与性质，解题关键是找到并证明全等三角形．

13．A

【分析】把代入解析式即可．

【详解】解：把代入得，

，

故选：A．

【点睛】本题考查了求一次函数的函数值，解题关键是把自变量的值代入后能准确熟练计算．

14．D

【分析】根据直角坐标系中点的平移特点即可求解.

【详解】点(2，−1)向右平移 1个单位得到的坐标为（3，-1），

故选D.

【点睛】此题主要考查坐标的平移，解题的关键是熟知直角坐标系中点的平移特点.

15．D

【分析】根据角平分线的判定定理，即可求解．

【详解】解：∵三角形三条角平分线的交点到三条边距离相等，

∴三角形内到三条边距离相等的点是三角形三条角平分线的交点．

故选：D

【点睛】本题主要考查了角平分线的判定定理，熟练掌握角的内部，到角两边距离相等的点在角平分线上是解题的关键．

16．A

【分析】根据已知和公共边科证明△ADB≌△ACD，则这两个三角形的对应角、对应边相等，据此即可解答．

【详解】∵AB＝AC，AD＝AD，AD⊥BC，

∴Rt△ADB≌Rt△ACD（HL），

∴BD＝CD，∠BAD＝∠CAD，∠B＝∠C（全等三角形的对应角、对应边相等）

故B、C、D一定成立，A不一定成立．

故选A．

【点睛】本题考查直角三角形全等的判定和性质，解决问题时注意利用已知隐含的条件AD是公共边．

17．A

【分析】根据比例系数，图象从左到右下降，与y轴交点在正半轴判断．

【详解】解: ∵比例系数，

∴图象从左到右下降，排除B和D选项；

∵一次函数图象经过，

与y轴交点在正半轴，

故选：A．

【点睛】本题考查了一次函数图象的性质，解题关键是根据系数k和b，确定一次函数图象的大致位置．

18．D

【分析】根据各象限内点的坐标特征进行判断即可得.

【详解】因

则点位于第四象限

故选：D.

【点睛】本题考查了平面直角坐标系象限的性质，象限的符号规律：第一象限、第二象限、第三象限、第四象限，熟记象限的性质是解题关键.

19．B

【分析】根据轴对称图形的概念：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形进行分析即可．

【详解】解：A、是轴对称图形，不合题意；

B、不是轴对称图形，符合题意；

C、是轴对称图形，不合题意；

D、是轴对称图形，不合题意．

故选：B．

【点睛】此题主要考查了轴对称图形，正确掌握轴对称图形的性质是解题关键．

20．B

【分析】根据三角形的三边关系定理逐项判断即可.

【详解】A、，不满足三角形的三边关系定理，此项不符题意

B、，满足三角形的三边关系定理，此项符合题意

C、，不满足三角形的三边关系定理，此项不符题意

D、，不满足三角形的三边关系定理，此项不符题意

故选：B.

【点睛】本题考查了三角形的三边关系定理：任意两边之和大于第三边，熟记定理是解题关键.

21．C

【分析】根据点的坐标的性质即可得.

【详解】由点的坐标的性质得，点P到x轴的距离为点P的纵坐标的绝对值

则点到轴的距离是

故选：C.

【点睛】本题考查了点的坐标的性质，掌握理解点的坐标的性质是解题关键.

22．D

【分析】根据三角形全等的判定定理逐项判断即可.

【详解】A、在和中，

则，此项不符题意

B、在和中，

则，此项不符题意

C、在和中，

则，此项不符题意

D、在和中，，但两组相等的对应边的夹角和未必相等，则不能证明，此项符合题意

故选：D.

【点睛】本题考查了三角形全等的判定定理，熟记各定理是解题关键.

23．C

【分析】根据对顶角的定义、同位角的定义、三角形的外角和、角平分线的性质逐项判断即可.

【详解】A、由对顶角的定义“如果一个角的两边分别是另一个角两边的反向延长线，且这两个角有公共顶点，那么这两个角是对顶角”可得，对顶角必相等，但相等的角未必是对顶角，此项不是真命题

B、只有当两直线平行，同位角必相等，此项不是真命题

C、根据内角和定理可知，任意多边形的外角和都为，此项是真命题

D、由角平分线的性质可知，角平分线上的点到角的两边距离相等，此项不是真命题

故选：C.

【点睛】本题考查了对顶角的定义、同位角的定义、三角形的外角和、角平分线的性质，熟记各定义和性质是解题关键.

24．A

【分析】根据孔庙和东山公园的位置，可知坐标轴的原点、单位长度、坐标轴的正方向，据此建立平面直角坐标系，从而可得体育场的位置.

【详解】由题意可建立如下图所示的平面直角坐标系：

平面直角坐标系中，原点O表示孔庙的位置，点A表示东山公园的位置，点B表示体育场的位置

则点B的坐标为

故选：A.

【点睛】本题考查了已知点在平面直角坐标系中的位置求其坐标，依据题意正确建立平面直角坐标系是解题关键.

25．C

【分析】加上EF后，原图形中具有△DEF了，故这种做法根据的是三角形的稳定性．

【详解】解：这种做法根据的是三角形的稳定性．

故选C．

【点睛】本题考查三角形稳定性的实际应用．三角形的稳定性在实际生活中有着广泛的应用，如钢架桥、房屋架梁等，因此要使一些图形具有稳定的结构，往往通过连接辅助线转化为三角形而获得．

26．D

【分析】根据一次函数的图象和性质，依次分析各个选项，选出正确的选项即可．

【详解】A．一次函数y=﹣3x﹣2的图象y随着x的增大而减小，即A项错误；

B．把x=0代入y=﹣3x﹣2得：y=﹣2，即在y轴的截距为﹣2，即B项错误；

C．把y=0代入y=﹣3x﹣2的：﹣3x﹣2=0，解得：x，即与x轴交于点（，0），即C项错误；

D．函数图象经过第二三四象限，不经过第一象限，即D项正确．

故选D．

【点睛】本题考查了一次函数图象上点的坐标特征，一次函数的性质，正确掌握一次函数图象的增减性和一次函数的性质是解题的关键．

27．C

【详解】解：当x＞1时，x+b＞kx+4，

即不等式x+b＞kx+4的解集为x＞1．

故选C．

28．D

【分析】先根据直角三角形的性质和角平分线的性质可得，再根据等边对等角可得，最后在中，利用直角三角形的性质即可得.

【详解】

平分

则在中，

故选：D.

【点睛】本题考查了等腰三角形的性质、角平分线的性质、直角三角形的性质：（1）两锐角互余；（2）所对的直角边等于斜边的一半；根据等腰三角形的性质得出是解题关键.

29．C

【分析】根据∠ABC=45°，CD⊥AB可得出BD=CD，利用ASA判定Rt△DFB≌Rt△DAC，从而得出DF=AD，BF=AC．则CD=CF+AD，即AD+CF=BD；再利用ASA判定Rt△BEA≌Rt△BEC，得出CE=AE=AC，又因为BF=AC所以CE=AC=BF，连接CG．因为△BCD是等腰直角三角形，即BD=CD．又因为DH⊥BC，那么DH垂直平分BC．即BG=CG．在Rt△CEG中，CG是斜边，CE是直角边，所以CE＜CG．即AE＜BG．

【详解】解：∵CD⊥AB，∠ABC＝45°，

∴△BCD是等腰直角三角形．

∴BD＝CD．故①正确；

在Rt△DFB和Rt△DAC中，

∵∠DBF＝90°﹣∠BFD，∠DCA＝90°﹣∠EFC，且∠BFD＝∠EFC，

∴∠DBF＝∠DCA．

又∵∠BDF＝∠CDA＝90°，BD＝CD，

∴△DFB≌△DAC．

∴BF＝AC；DF＝AD．

∵CD＝CF+DF，

∴AD+CF＝BD；故②正确；

在Rt△BEA和Rt△BEC中

∵BE平分∠ABC，

∴∠ABE＝∠CBE．

又∵BE＝BE，∠BEA＝∠BEC＝90°，

∴Rt△BEA≌Rt△BEC．

∴CE＝AE＝AC．

又由（2），知BF＝AC，

∴CE＝AC＝BF；故③正确；

连接CG．

∵△BCD是等腰直角三角形，

∴BD＝CD

又DH⊥BC，

∴DH垂直平分BC．

∴BG＝CG

在Rt△CEG中，

∵CG是斜边，CE是直角边，

∴CE＜CG．

∵CE＝AE，

∴AE＜BG．故④错误．

∴正确的选项有①②③；

故选：C．

【点睛】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、AAS、ASA、HL．在复杂的图形中有45°的角，有垂直，往往要用到等腰直角三角形，要注意掌握并应用此点．