专题15 一次函数中的存在性问题-【重难点突破】2022-2023学年八年级数学上册常考题专练（北师大版）

这是一份专题15 一次函数中的存在性问题-【重难点突破】2022-2023学年八年级数学上册常考题专练（北师大版），文件包含专题15一次函数中的存在性问题解析版-重难点突破2022-2023学年八年级数学上册常考题专练北师大版docx、专题15一次函数中的存在性问题原卷版-重难点突破2022-2023学年八年级数学上册常考题专练北师大版docx等2份试卷配套教学资源，其中试卷共88页， 欢迎下载使用。
专题15 一次函数中的存在性问题
目录
题型一 等腰三角形存在性问题
题型二 等腰直角三角形存在性问题
题型三 45°角的存在性问题
题型四 直角三角形存在性问题
题型五 全等三角形存在性问题


题型一 等腰三角形存在性问题
1．如图，一次函数的图象经过点，．以线段为边在第一象限内作等腰直角三角形，．若第二象限内有一点，且的面积与的面积相等．
（1）求直线的函数表达式．
（2）求的值．
（3）在轴上是否存在点，使为等腰三角形，若存在，直接写出点的坐标；若不存在．请说明理由．

【解答】解：（1）设直线的解析式为，
将点，代入解析式，
得，解得，
直线的解析式为；
（2）如图，过点作轴交于点，
，，
，，
等腰直角三角形，，
由勾股定理可得，
，
，，

，
的面积与的面积相等，
，
；
（3）①当时，过点作轴交于点，

，，
，
，
，
，
，
，
是等腰三角形边的中点，
，
；
②当时，
，
，
或；
③当时，作的垂线平分线，分别交、轴于点、，

，
，
，
，
，即，
，
，
，；
综上所述：为等腰三角形时，点的坐标为或或，或．

2．如图，在平面直角坐标系中，直线向下平移1个单位后，得到直线，交轴于点，点是直线上一动点，过点作轴交于点
（1）求出点的坐标；
（2）连接，当为以为底边的等腰三角形时，求点和点的坐标；
（3）点为的中点，连接、，若点在轴的左侧，为直线上一动点，当与全等时，求点的坐标．

【解答】解：（1）直线向下平移1个单位后，得到直线，
直线的解析式为，
交轴于点，
；
（2）当为以为底边的等腰三角形时，
，
点是直线上一动点，
设点，
过点作轴交于点
，
，
，
，；
（3）点为的中点，
，
，
设，，则，
，，
，，
与全等，
①当时，
有，，
，，
，
或，
或；
②当时，
有，，
，，
，
点在轴的左侧，
，
此时不存在；
综上所述，或．
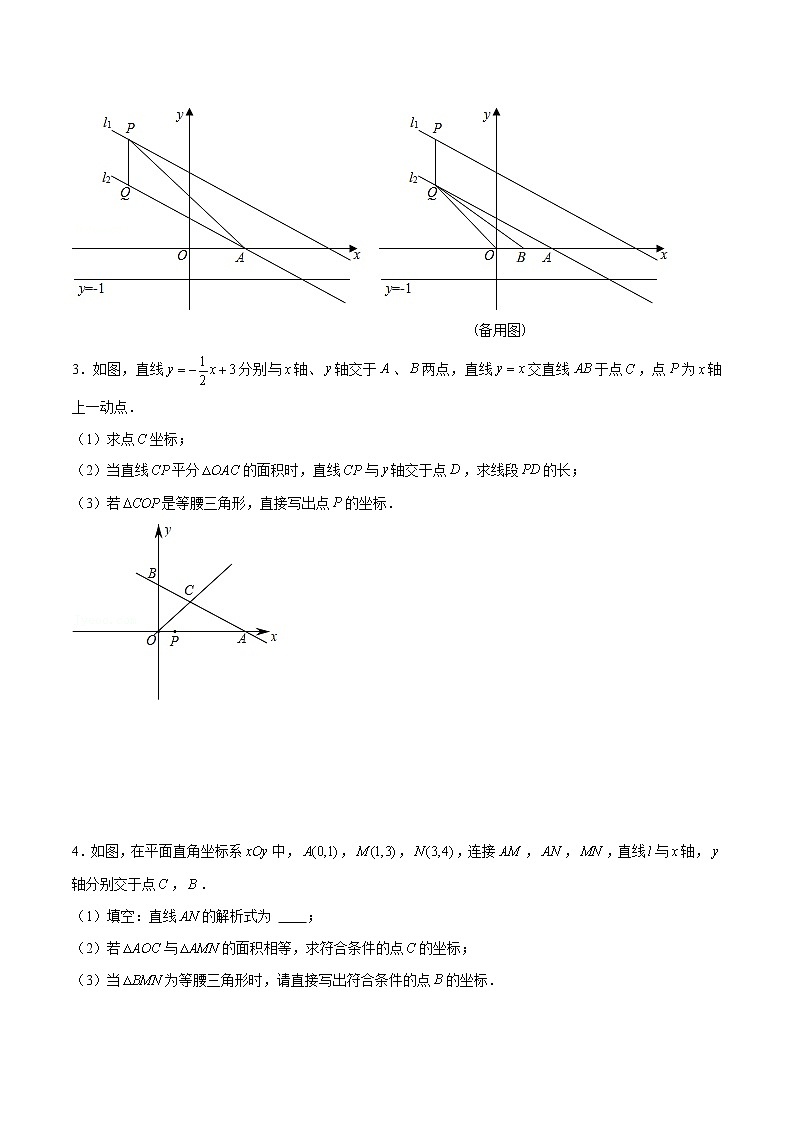
3．如图，直线分别与轴、轴交于、两点，直线交直线于点，点为轴上一动点．
（1）求点坐标；
（2）当直线平分的面积时，直线与轴交于点，求线段的长；
（3）若是等腰三角形，直接写出点的坐标．

【解答】解：（1）直线交直线于点，
联立方程组，
解得：，
；
（2）如图，

直线分别与轴、轴交于、两点，
令，则，解得，
令，则，
，，
，
点为轴上一动点．直线平分的面积，
设，则，
，即，
，即，，
设直线的解析式为，
由题意可得：，
解得：，
直线的解析式为，
，
，
轴轴，即，
又，，
；
（3），
，
是等腰三角形，
此题有三种情形：
①当时，如图①，则，或，；
②当时，过点作（或轴）于点，如图②，
则，即，
；
③当时（即作的中垂线交轴于点，如图③，
又直线与轴夹角，
，
，即轴，
，
；
综上所述，，或，或或．



4．如图，在平面直角坐标系中，，，，连接，，，直线与轴，轴分别交于点，．
（1）填空：直线的解析式为 　　；
（2）若与的面积相等，求符合条件的点的坐标；
（3）当为等腰三角形时，请直接写出符合条件的点的坐标．

【解答】解：（1）设直线的表达式为，
则，解得，
故直线的表达式为，
故答案为：；

（2）延长交轴于点，

由点、的坐标，同理可得，直线的表达式为，
故点，则，
则的面积，
而的面积的面积，
解得，
故点；

（3）设点，
由点、、的坐标得：，，，
当时，则，解得；
当时，则，解得或1，
当时，则，无解；
综上，点的坐标为或或．
5．如图1，在平面直角坐标系中，是坐标原点，长方形的顶点、分别在轴与轴上，已知，．点为轴上一点，其坐标为，点从点出发以每秒2个单位的速度沿线段的方向运动，当点与点重合时停止运动，运动时间为秒．
（1）当点经过点时，求直线的函数解析式；
（2）①求的面积关于的函数解析式；
②如图2，把长方形沿着折叠，点的对应点恰好落在边上，求点的坐标．
（3）点在运动过程中是否存在使为等腰三角形？若存在，请求出点的坐标；若不存在，请说明理由．

【解答】解：（1），，四边形为长方形，
．
设此时直线解析式为，
把，分别代入，得
，
解得
则此时直线解析式为；

（2）①当点在线段上时，，高为6，；
当点在线段上时，，高为，；
②设，则，如图2，
，，
，
，
，
，解得
则此时点的坐标是，；

（3）存在，理由为：
因为，所以满足条件的点上．
若为等腰三角形，分三种情况考虑：如图3，
①当，
在中，，，
根据勾股定理得：，
，即；
②当时，此时；
③当时，
在中，，
根据勾股定理得：，
，即，，
综上，满足题意的坐标为或，或．



6．如图，直线与轴轴分别交于、两点在轴上有一点，是上一点．
（1）点的坐标：　　；点的坐标 　　；
（2）若，求直线的表达式；
（3）在（2）的条件下，轴上是否存在点，使得是等腰三角形？若存在，求出所有符合条件的点的坐标；若不存在，请说明理由．

【解答】解：（1）令，由，得，
；
当时，，
．
故答案为：；．
（2）如图1，作直线，射直线的函数表达式为，
，
，
是上一点，
；
把、代入得，
，
直线的表达式为．
（3）存在，如图2，，则垂直平分，
，
；
如图3，，点与点在直线的同侧，
，，，
，
，
，
，；
如图4，，点与点在直线的异侧，
，
，
，；
如图5，，
，
，
，
，
，
解得，，
．
综上所述，点的坐标为或，或，或．




7．如图①，在平面直角坐标系中，的边在轴上，点坐标为，点在第一象限，，．为射线上一点，过作直线轴交于，交射线于．
（1）求点坐标；
（2）当为线段中点时，在直线上找点，当为等腰三角形，请直接写出点坐标；
（3）如图②，为中点，当时，求点坐标．

【解答】解：（1）如图①，过点作于，
，，
，
，
，
，
；

（2），
，
点是中点，
，，
，
设，
，
，，，
为等腰三角形，
①，
，
或，
或，
②，
，
，

③，
，
（舍或，
，
即：满足条件的点或或或；

（3）如图
由（1）知，，
直线的解析式为，
，
直线的解析式为，
点是中点，
，
设点，，
，
，
，
，
或，
或．



题型二 等腰直角三角形存在性问题
8．已知一次函数的图象与轴交于点，与轴交于点，且的面积为4，函数值随自变量的值增大而减小．
（1）求直线的表达式，并画出函数图象；
（2）以线段为底边在第一象限作等腰直角三角形，求点的坐标．

【解答】解：（1）令，则，
一次函数与轴交点，
，
，
，
，
函数值随自变量的值增大而减小，
，
将代入到一次函数解析式中得，，
直线的表达式为，函数图象如图1；
（2）如图2，线段为底边在第一象限作等腰直角三角形，
过作轴于，过作轴于，
，
四边形为矩形，
，
，
，
在与中，
，
，
，，
矩形为正方形，
，
，
，
．


9．如图，已知长方形的顶点在坐标原点，、分别在、轴的正半轴上，点的坐标为，直线分别边、轴交于、两点．连接，与直线交于点．
（1）求所在的直线的解析式；
（2）在直线上找一点，使的面积等于的面积，请求出点的坐标；
（3）已知点在第一象限，且是直线上的点，点是边上一点，若是等腰直角三角形，求点的坐标．

【解答】解：（1）长方形，点的坐标为，
，，
点的坐标为，点的坐标为．
设直线的解析式为：，
将、代入得：，
解得：，
．
（2）将直线和联立成方程组得：，
解得：，
点的坐标是：．
将代入直线得：．
点的坐标为．
，
，
，
将代入直线得：，
解得：，
点的坐标为，
点在直线上，
设点的坐标为，
当点在上方时，
，
解得：，
，
点的坐标为，
当点在下方时，
，
解得：，
，
点的坐标为，
综上所述点的坐标为或．
（3）①当，时，如图①，
过点、作轴的垂线，垂足为、，
，
，
，
，
，
在和中，
，
，
，，
设，
点坐标为，
，
解得：，
点在边上，
，
，不会题意，舍去．
②当，时，如图②，设，
过点作，交的延长线于点，
则，
，
，
，
，
在和中，
，
，
，，
，到轴的距离为，
点的坐标为，
点在直线上，
，
解得：，
点的坐标为．③当，时，如图③，
过点作轴，垂足为点，延长交直线于点，
则，
，
，
，
，
在和中，
，
，
，，
设，
当点在上方时，
，
，
点的坐标为，
，
解得：，
点的坐标为．
当点在下方时，
，
，
点的坐标为，
，
解得：，
点的坐标为．
综上所述点的坐标为、或．



10．在直角坐标平面中，任意线段的中点坐标可以用这条线段的两个端点的坐标来表示，若平面内点，，点，，则线段的中点坐标可以表示为，，如图，直线与轴交于点，与轴交于点，点是线段的中点．
（1）求点的坐标．
（2）点在轴上，且，求直线的表达式．
（3）在平面直角坐标系内，直线下方是否存在一点，使得是等腰直角三角形，若存在，请直接写出点的坐标，不存在，请说明理由．

【解答】解：（1）直线与轴交于点，与轴交于点，
，，
，，
；
（2）如图，

，，
，，
在中，，
点是线段的中点，
，
，
，
，
，
，
，即，
，
，
，
点的坐标为，
设直线的表达式为，将代入得：，解得：，
直线的表达式为；
（3）分别过点，点作的垂线，在直线下方截取，，连接，交于，

，，，，
、是等腰直角三角形，
，
，，
是等腰直角三角形，
过点，作轴于，轴于，
，，
，
，，
，
，，
，
点的坐标，
同理点的坐标，
，
点的坐标，，即，
综上，点的坐标为或或．
11．如图，在平面直角坐标系中，直线经过点，，交轴于点；
（1）求直线的关系式；
（2）求的面积；
（3）作等腰直角三角形，使，求出点的坐标．

【解答】解：（1）设直线解析式为，
直线经过点，，
，
，
直线的解析式：；
（2）直线交轴于点，
点，
，
，
，
；
（3）如图，当点在直线下方时，过点作轴于，

，
，
，
又，，
，
，，
，
点，
当点在直线上方时，同理可得：，，
，
点，
综上所述：点或．
12．在平面直角坐标系中，直线与轴、轴分别交于点、两点，，直线经过点，与轴、轴和线段分别交于点、、三点．
（1）求直线的解析式；
（2）如图①：若，求点的坐标和的面积；
（3）如图②：在坐标轴上是否存在点，使是以为底边的等腰直角三角形，若存在，请直接写出点的坐标；若不存在，请说明理由．

【解答】解：（1）直线与轴点，
，，
，
，
，
把代入得到，，
直线的解析式为．

（2）如图1中，作于，于．

，，，
，

，
，
当时，，
解得，
，
把，代入，得到，
解得，
直线的解析式为，
，
．

（3）①如图③中，当，时，作于，轴于．设．

，
，，
，
，
，
，，
，，
把点坐标代入，得到：，
解得，
，．

②如图③中，当，时，作于，于．设．

同法可证：，
，，
，，
把点坐标代入，得到：，
解得
，．
③如图③中，当点在则的负半轴上时，作于，于．设．

同法可得，，把点坐标代入，得到：，解得，
，，此时点在第二象限，不符合题意舍弃．
综上所述，满足条件的点坐标为，或，．

题型三 45°角的存在性问题
13．（1）如图1，在四边形中，，点是边上一点，，，连接、，求证是等腰直角三角形．
（2）如图2，一次函数的图象与轴交于点，与轴交于点，直线交轴于点，且，则点的坐标为　　．

【解答】（1）证明：在和中，
，
，
，，
在中，，
．
．
，
．
是等腰直角三角形；
（2）解：如图2，过点作，交于点，过点作，交于点，

把代入中，得，
点的坐标为，
，
把代入，得，解得，
点的坐标为，
，
，，
，
，
，，
，，
又，
，
在和中，
，
，
，，
，
点的坐标为，
设直线的解析式为，
由题意可得，
解得，
直线的解析式为，
令，解得，
．
14．如图1，直线的解析式为，点坐标为，点关于直线的对称点点在直线上．
（1）求直线、的解析式．
（2）如图2，若交于点，在线段上是否存在一点，使与的面积相等，若存在求出点坐标；若不存在，请说明理由．
（3）如图3，过点的直线，当它与直线夹角等于时，求出相应的值．

【解答】解：（1），
，
，
，
，
直线的解析式为，
在中，，
点、点关于直线对称，
设，，，
，
在中，，
，
，
直线的解析式为；
（2）点在直线上，
设，
，，
，
，
，
，，
直线的解析式为，
与的面积相等，
与的面积相等，
，
设直线的解析式为，
在直线上，
，
直线的解析式为，
联立，
，
；
（3）设直线、与直线夹角等于，
为等腰直角三角形，
作于，于，
，
，，
直线经过，
，
设，则，，
，
点在直线上，
，
，
，，
当直线经过点时，，解得，
当直线经过点时，，解得，
或．

15．已知一次函数．

（1）该函数图象一定经过定点，求点坐标；
（2）该函数经过点，
①若点为轴上一点，，求点坐标；
②若点为该函数上一点，且，求点坐标；
【解答】解：（1），
时，，
．
（2）①把点代入，得：
，解得：，
直线解析式为：，
当时，，
直线与轴的交点为，
设点，则，
，
，
解得：，，
，，
②过点作垂直于点，
，，
，，，
，
，
解得：，
，
为等腰直角三角形，
，
设点，
，
解得：，，
当时，，
当时，，
，
此时，点在点的下方，，不符合题意，
，．


16．在平面直角坐标系中，直线分别交轴，轴于，，且满足．
（1）求，的值；
（2）点在直线的右侧，且．
①若点在轴上（图，求点的坐标；
②若为直角三角形，求点的坐标．

【解答】解：（1），
，
，；
（2）①如图1中，
，，
，
．
故答案为．
②，

又为直角三角形，
只有两种情况，或
①如图2中，若，过点作，垂足为．

，
又，
，
，
又，
，
，
，，
，
．
②如图3中，若，过点作，垂足为．

，
又，
，
，
又，
，
，
，
，，
，
．
综上述，点坐标为，．
17．【模型建立】如图1，等腰直角三角形中，，直线经过点，过点作于点，过点作于点，易证明（无需证明），我们将这个模型称为“形图”．接下来我们就利用这个模型来解决一些问题：
【模型运用】（1）如图2，在平面直角坐标系中，等腰，，，与轴交点，点的坐标为，点的坐标为，求，两点坐标；

（2）如图3，在平面直角坐标系中，直线函数关系式为：，它交轴于点，交轴于点，在轴上是否存在点，使直线与直线的夹角为？若存在，求出点的坐标；若不存在，请说明理由．
【模型拓展】（3）如图4，在中，，，，点在上，点在上，，分别连接，交于点．若，请直接写出的长．

【解答】解：（1）如图1，过点作轴于，
点的坐标为，点的坐标为，
，，
等腰，，，
又轴，轴轴，
，
，，
，
在和中，
，
，
，，
，
，
设直线的解析式为，
，，
，
，
直线的解析式为，
与轴交点，
；
（2）存在符合条件的点．理由如下：
①点在负半轴上，如图2，
过点作，交于点，过点作轴于点，
，，
，
，
，，
，
，
，，
，
，
设直线的解析式为，
，，
，
解得：，
直线的解析式为，
，；
②点在正半轴上，如图3，
过点作交于点，过点作轴于点，
，，
，
，
，，
，
，
，，
，
，
设直线的解析式为，
，，
，
解得：，
直线的解析式为，
，；
综上所述，，或，；
（3）如图4，过点作，过点作于交轴于，
在轴负半轴上截取，过点作轴交的延长线于，
则，
，，
，
，
，，
，，
，
在和中，
，
，
，
，
设直线解析式为，
，，
，
解得：，
直线解析式为，
令，得，
解得：，
，，
，
在中，，
设，则，
，
，
，，
是等腰直角三角形，
，
在中，，
，
解得：（舍去），，
，，
．





题型四 直角三角形存在性问题
18．如图，在平面直角坐标系中，函数的图象与轴，轴分别交于点，，与函数的图象交于点．
（1）求和的值；
（2）函数的图象与轴交于点，点从点出发沿方向，以每秒2个单位长度匀速运动到点（到停止运动）．设点的运动时间为秒．
①当的面积为12时，求的值；
②在点运动过程中，是否存在的值，使为直角三角形？若存在，直接写出的值；若不存在，请说明理由．

【解答】解：（1）点在直线上，
，
点，
函数的图象过点，
，得，
即的值是4，的值是；
（2）①函数的图象与轴，轴分别交于点，，
点，点，
函数的图象与轴交于点，
点的坐标为，
，
的面积为12，
，
解得，．
即当的面积为12时，的值是5；
②当或时，是直角三角形，
理由：当时，，
点，点，点，点，
，，
，
，
，
，
，
，
，
解得，；
当时，
，，
，
，
，
解得，；
由上可得，当或时，是直角三角形．
19．如图1，在平面直角坐标系中，点坐标为，点的坐标为．
（1）求线段的长；
（2）点是坐标轴上的一个点，若以为直角边构造直角三角形，请求出满足条件的所有点的坐标；
（3）如图2，以点为直角顶点作，射线交轴的负半轴与点，射线交轴的负半轴与点，当绕点旋转时，的值是否发生变化？若不变，直接写出它的值；若变化，直接写出它的变化范围（不要求写解题过程）．

【解答】解：（1）如答图1，过点作轴于，
，
，，
，
，
在中，根据勾股定理得，；

（2）如答图2，当点在轴上时，设点，
点，，
，，
由（1）知，，
是以为直角边的直角三角形，
，
，
，
，，
当点在轴上时，设，
点，，
，，
由（1）知，，
是以为直角边的直角三角形，
当时，，
，
，
，
当时，，
，
，
，
即满足条件的点，或或；

（3）的值不发生变化，理由：
过点作轴于，则，，，，
，，
，
，
，
，
，
即的值不变，定值为8．



20．如图，在中，以为原点构建直角坐标系，点在轴上，与轴交于点，已知，．
（1）求直线的解析式；
（2）求点的坐标；
（3）在轴上是否存在点，使得是直角三角形？若存在，求出点的坐标；若不存在，请说明理由．

【解答】解：（1）由条件可得：，，
设直线的解析式为：，则，解得：，
直线的解析式为：；

（2）设点，则，解得：，
点的坐标为；

（3）存在，理由如下：
设点为，，
，，
由题意可得是直角三角形需分两种情况讨论：
①，此时点的坐标为；
②，，
即，解得：，
此时点的坐标为；
综上所述，存在满足条件的点的坐标为或．
21．如图，直线交轴于点，直线交轴于点，两直线交于点，根据图中的信息解答下列问题：
（1）不等式的解集是　　，不等式组的解集是　　；
（2）求点的坐标；
（3）若过点的直线与轴交于点，当以、、为顶点的三角形是直角三角形时，求直线的解析式．

【解答】解：（1）直线交轴于点，
不等式的解集是，
直线交轴于点，
不等式的解解为，
直线交轴于点，
不等式的解集为，
不等式组的解集是，
故答案为：；；

（2）直线交轴于点，
，则，
，
直线交轴于点，
，则，
，
解方程组，得，
；

（3）如图，当时，
，
，
直线为：，
当时，，
设点，
如图，直线为与轴交于点，
，
则，
由（2）知，，
，，

，
，
设直线的解析式为，
则，解之：
直线的解析式为：．

22．如图，在平面直角坐标系中，过点的直线与直线相交于点动点沿路线运动．
（1）求直线的解析式；
（2）当的面积是的面积的时，求出这时点的坐标；
（3）是否存在点，使是直角三角形？若存在，直接写出点的坐标，若不存在，请说明理由．

【解答】解：（1）点的坐标为，
设直线的解析式为，
点在直线上，
，
，
直线的解析式为；

（2）由（1）知，直线的解析式为，
令，
，
，
，
，
的面积是的面积的，
，
设的纵坐标为，
，
，
，
直线的解析式为，
当点在上时，，
，，
当点在上时，，
，
即：点，或；

（3）是直角三角形，
，
①当点在上时，如图，过点作轴于，
，
，
，
，
由（2）知，直线的解析式为①，
设点的坐标为，
，
，

，，
②当点在上时，同①的方法，
，
即：点的坐标为，或．

23．如图，在平面直角坐标系中，函数的图象与轴，轴分别交于点，，与函数的图象交于点．

（1）求和的值；
（2）函数的图象与轴交于点，点从点出发沿方向，以每秒2个单位长度匀速运动到点（到停止运动）．设点的运动时间为秒．
①当的面积为12时，求的值；
②在点运动过程中，是否存在的值，使为直角三角形？若存在，直接写出的值；若不存在，请说明理由．
【解答】解：（1）点在直线上，
，
点，
函数的图象过点，
，得，
即的值是4，的值是；
（2）①函数的图象与轴，轴分别交于点，，
点，点，
函数的图象与轴交于点，
点的坐标为，
，
由题意可得，，则，
由，得，
则点的坐标为，
的面积为12，
，
解得，
即当的面积为12时，的值是5；
②当或时，是直角三角形，
理由：当时，，
点，点，点，点，
，，
，
，
，
，
，
，
，
解得，；
当时，
，，
，
，
，
解得，；
由上可得，当或时，是直角三角形．

24．已知，如图1，在平面直角坐标系中，矩形的边在轴的正半轴上，在轴的正半轴上，，，过原点作的平分线交于点，连接，过点作，交于点．
（1）求经过点、的直线解析式；
（2）将绕点按顺时针方向旋转后，角的一边与轴的正半轴交于点，另一边与线段交于点，使得，请求出此时的长度．
（3）对于（2）中的点，在直线上是否存在点，使得点与点、构成的是直角三角形？若存在，请求出点的坐标；若不存在，请说明理由．

【解答】解：（1）如图1中，

四边形是矩形，
，
，
，，
，
，
，
，
，
平分，
，
，
，
又，
，
，
，
设直线的解析式为，则有，
解得
直线的解析式为

（2）如图2中，作于．

易知，
，设，则，
，
，
，
，
．

（3）如图3中，

①作于，则是直角三角形．
，，
直线的解析式为，
由，解得，
，．
②作交直线于，则是直角三角形，
直线的解析式为，
直线的解析式为，
由，解得，
，，
综上所述，满足条件的点坐标为，或，．

题型五 全等三角形存在性问题
25．如图，一次函数的图象与轴、轴分别交于点、，线段的中点为．将沿直线折叠，使点与点重合，直线与轴交于点．
（1）求此一次函数的解析式；
（2）求点的坐标；
（3）在坐标平面内存在点（除点外），使得以、、为顶点的三角形与全等，请直接写出点的坐标．

【解答】解：（1）设点坐标为，点坐标为，
由线段的中点为，得
，，
解得，．
即，，
一次函数的解析式为．
（2）如图1：连接，设，则，

，
，
，
解得，
即，；
（3）①当时，设，
由是的中点，得
，，
解得，，
即，；
如图，
②当△时，
做与，与点，，，
由△，
，，
，
，；
③当△时，设
是线段的中点，得
，，
解得，，
即，，
综上所述：，；，；，．
26．如图，一次函数的图象与轴和轴分别交于点和，再将沿直线对折，使点与点重合、直线与轴交于点，与交于点．
（1）点的坐标为　　，点的坐标为　　；
（2）求的长度；
（3）在坐标平面内，是否存在点（除点外），使得与全等？若存在，请求出所有符合条件的点的坐标；若不存在，请说明理由．

【解答】解：（1）令，则，
，
令，则，
，
，
故答案为：，；

（2）设，
，
由折叠知，，
在中，，
根据勾股定理得，，
，
，
即：，

（3）设，
，，
，，
与，
①，
，，
，
（舍或，
，；
②，
，，
，，
或，
或，，
即：满足条件的点或，或，．
27．如图①，已知直线与轴、轴分别交于点、，以、为边在第一象限内作长方形．
（1）求点、的坐标；
（2）将对折，使得点与点重合，折痕交于点，求直线的解析式（图②；
（3）在坐标平面内，是否存在点（除点外），使得与全等？若存在，请求出所有符合条件的点的坐标；若不存在，请说明理由．

【解答】解：（1）；（2分）

（2）由折叠知：．设，则，，
根据题意得：解得：
此时，，（2分）
设直线为，把代入得（1分）
解得：
直线解析式为（1分）

（3）①当点与点重合时，，此时
②当点在第一象限时，如图，
由得，
则点在直线上．过作于点，
在中，
，，
由得：

，把代入得
此时
（也可通过勾股定理求长得到点的纵坐标）
③当点在第二象限时，如图
同理可求得：

此时
综合得，满足条件的点有三个，
分别为：；；．


28．在平面直角坐标系中，已知点的坐标为，点的坐标为．
（1）求直线的表达式；
（2）若点的坐标为，且，求的值；
（3）若点的坐标为，在射线上有两点，，使得以，，为顶点的三角形与全等，求点的坐标．

【解答】解：（1）设直线的表达式为，
点、在直线上，
，
，
，
直线的表达为；
（2）过轴上的点作轴平行线，交于，如图：

点的坐标为，
点的纵坐标为9，
当时，，解得，
，
，



，
，
，
解得或；
（3）①当点在线段上时，
若点在，之间，如图：

，，
，
设中边上的高为，
则，
，即，
当时，，，，此时，
，，
当时，，
；
若点在，之间，如图：

当，且时，有，
，
，
，
，
作于，则，
，
，
当时，，解得，
；
②当点在的延长线上时
若点在，之间，

当，时，，
作于，于，
，且，，
，
，
，
当时，，解得，

若点在的延长线上或的反向延长线上，都不存在满足条件的，两点；
综上所述，满足条件的点为或或．