人教版七年级上册第一章 有理数综合与测试学案

这是一份人教版七年级上册第一章 有理数综合与测试学案，共19页。学案主要包含了知识呈现，知识归纳，知识运用等内容，欢迎下载使用。

第3讲 有理数的乘除及乘方


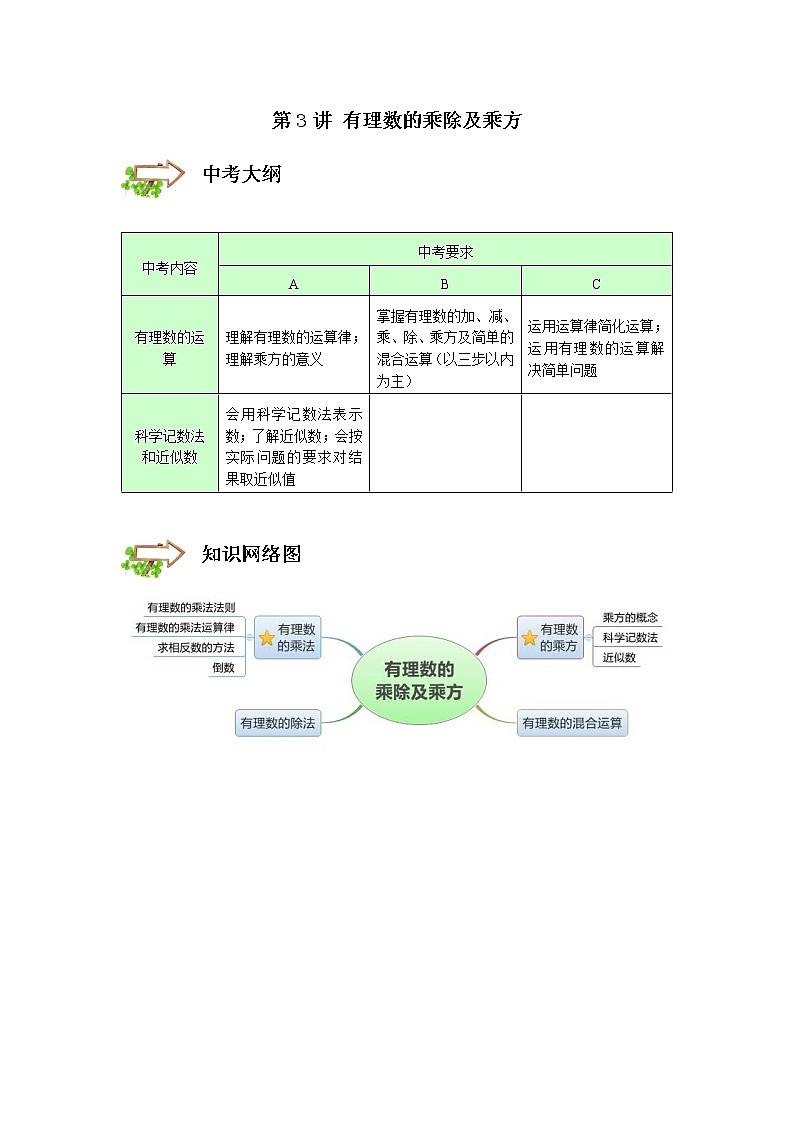
中考内容
中考要求
A
B
C
有理数的运算
理解有理数的运算律；理解乘方的意义
掌握有理数的加、减、乘、除、乘方及简单的混合运算（以三步以内为主）
运用运算律简化运算；运用有理数的运算解决简单问题
科学记数法和近似数
会用科学记数法表示数；了解近似数；会按实际问题的要求对结果取近似值



知识网络图




1有理数的乘法
知识概述
中考大纲


一． 有理数的乘法
1. 有理数乘法法则：两数相乘，同号得正，异号得负，并把绝对值相乘．
任何数同相乘，都得．
2. 有理数乘法的运算步骤：先确定积的符号，再确定积的绝对值．
3. 有理数乘法的应用：要得到一个数的相反数，只要将它乘．
4. 多个有理数相乘：
（1） 几个不是的数相乘，负因数的个数是偶数时，积为正数；负因数的个数是奇数时，积为负数，即“奇负偶正”．
（2） 几个数相乘，如果其中有因数为，那么积等于．
5. 有理数乘法运算律：
（1） 乘法交换律：一般地，有理数乘法中，两个数相乘，交换因数的位置，积相等．

（2） 乘法结合律：一般地，有理数乘法中，三个数相乘，先把前两个数相乘，或者先把后两个数相乘，积相等．

（3） 分配律：一般地，有理数乘法中，一个数同两个数的和相乘，等于把这个数分别同这两个数相乘，再把积相加．

二． 倒数
1． 倒数的概念：乘积是的两个数互为倒数．
（1） 倒数是成对出现的，单独一个数不能称为倒数．
（2） 互为倒数的两个数的乘积一定是，即，互为倒数，则；反之亦然．
（3） 没有倒数．
2． 求一个非零有理数的倒数，把它的分子和分母颠倒位置即可．
（1） 非零整数可以看作分母为的分数；
（2） 带分数一定要先化成假分数之后再求倒数．
小试牛刀


【例】（2017秋•鞍山期末）若“！”是一种数学运算符号，并且1！=1，2！=2×1=2，3！=3×2×1=6，4！=4×3×2×1，…，则的值为（　　）
A． B．49！ C．2450 D．2！
【解答】解：==50×49=2450
故选：C．
再接再厉


【例】（2016秋•吉林期末）已知a、b为有理数，ab≠0，且M=，当a、b取不同的值时，M的值是（　　）
A．±2 B．±1或±2 C．0或±1 D．0或±2
【解答】解：当a＞0、b＞0时，M=1+1=2；
当a＞0、b＜0时，M=1﹣1=0；
当a＜0、b＞0时，M=﹣1+1=0；
当a＜0、b＜0时，M=﹣1﹣1=﹣2；
综上，M的值是0或±2，
故选：D．
【练习】（2017秋•海拉尔区校级月考）（﹣0.25）×（﹣）×4×（﹣18）．
【解答】解：原式=﹣（××4×18）=﹣14．
【巩固】（2017秋•金堂县月考）用简便方法计算：（﹣9）×18．
【解答】解：原式=（10﹣）×（﹣18）=﹣180+=﹣179．
总述

思考：多个不是的数相乘，先做哪一步，再做哪一步？


2有理数的除法
知识概述


一． 有理数的除法
1. 有理数除法法则：
（1） 除以一个不等于的数，等于乘这个数的倒数．
，()
（2） 法则的另一说法：两数相除，同号得正，异号得负，并把绝对值相除．
除以任何一个不等于的数，都得．
2. 有理数除法的运算步骤：先将除法换成乘法，然后确定积的符号，最后求出结果．
3. 分数：分数可以理解为分子除以分母．
二． 有理数的乘除混合运算
先将除法换成乘法，然后确定积的符号，最后求出结果．
注意：乘除混合运算要“从左到右”运算．
小试牛刀


【例】（2017秋•海淀区校级期中）．
【解答】解：===．
【巩固】（2017秋•沙雅县校级期中）0÷．
【解答】解：0÷．
=0×[15×（2﹣4）÷×]2
=0．
再接再厉


【例】（2017秋•盐都区校级月考）阅读下列材料：
计算：÷﹙﹣+﹚．
解法一：原式=÷﹣÷+÷=×3﹣×4+×12=．
解法二：原式=÷﹙﹣+﹚=÷=×6=．
解法三：原式的倒数=﹙﹣+﹚÷=﹙﹣+﹚×24=×24﹣×24+×24=4．
所以，原式=．
（1）上述得到的结果不同，你认为解法____是错误的；
（2）请你选择合适的解法计算：﹙﹣﹚÷﹙﹣+﹣﹚．
【解答】解：（1）上述得到的结果不同，我认为解法一是错误的；
故答案为：一；
（2）原式的倒数为原式的倒数为：（﹣+﹣）÷（﹣）=（﹣+﹣）×（﹣42）=﹣7+9﹣28+12=﹣35+21=﹣14，
则原式=﹣．
　
【例】（2017秋•莘县校级月考）阅读下列材料：计算：÷（﹣+）
解：原式的倒数为
（﹣+）÷
=（﹣+）×12
=×12﹣×12+×12
=2
故原式=
请仿照上述方法计算：（﹣）÷（﹣+﹣）
【解答】解：原式的倒数为
（﹣+﹣）÷（﹣）
=（﹣+﹣）×（﹣42）
=（﹣42）×﹣（﹣42）×+（﹣42）×﹣（﹣42）×
=﹣7+9﹣28+12
=﹣14，
故原式=﹣．
　总述

思考：加减乘除混合运算的运算顺序是什么？



3有理数的乘方
知识概述


一． 有理数的乘方
1. 乘方的概念：求个相同因数的积的运算叫做乘方，乘方的结果叫做幂．
（1） 一般地，个相同的因数相乘，即，记作，读作“的次方”；
（2） 在中，叫做底数，叫做指数；
（3） 当看作的次方的结果时，读作的次幂．
注意：，其底数为，；
，其底数为，；
，其底数为，；
，其底数为，；
，带分数的乘方运算，一定要先化成假分数后再运算．
2. 一个数可以看作这个数本身的一次方，例如，就是，指数通常省略不写．
3. 幂的正负规律：
（1） 负数的奇次幂是负数，负数的偶次幂是正数，即“奇负偶正”；
（2） 正数的任何次幂都是正数；
（3） 0的任何正整数次幂都是0．
二． 科学记数法
1． 科学记数法：把一个大于的数表示成的形式（其中，是正整数）．
2． 用科学记数法表示一个位整数，其中的指数是，的指数比整数的位数少．
3． 万，亿
三． 近似数
1． 准确数：表示实际数量的数．
2． 近似数：在一定程度上反映被考察量的大小，能说明实际问题的意义，与准确数非常地接近．
3． 精确度：表示近似数与准确数的接近程度．
4． 精确度的类型：
（1） 纯数字类
按四舍五入法对圆周率取近似数时
（精确到个位）
（精确到十分位，或叫精确到）
（精确到百分位，或叫精确到）
（精确到千分位，或叫精确到）
（2） 带单位类
近似数万（精确到千位）
（3） 科学记数法类
近似数（精确到百位）

小试牛刀


【例】（2018•思南县一模）下列各组的两个数中，运算后结果相等的是（　　）
A．23和32 B．﹣33和（﹣3）3 C．﹣22和（﹣2）2 D．和
【解答】解：A、23=8，32=9，故本选项错误；
B、﹣33=﹣27，（﹣3）3=﹣27，故本选项正确；
C、﹣22=﹣4，（﹣2）2=4，故本选项错误；
D、=﹣，=﹣，故本选项错误．
故选：B．
　
再接再厉


【例】阅读材料，求值：1+2+22+23+24+…+22015．
解：设S=1+2+22+23+24+…+22015，将等式两边同时乘以2得：
2S=2+22+23+24+…+22015+22016
将下式减去上式得2S﹣S=22016﹣1
即S=1+2+22+23+24+…+22015=22016﹣1
请你仿照此法计算：
（1）1+2+22+23+…+210
（2）1+3+32+33+34+…+3n（其中n为正整数）
【解答】解：（1）设S=1+2+22+23+24+…+210，
将等式两边同时乘以2，得
2S=2+22+23+24+…+211
将下式减去上式，得
2S﹣S=211﹣1
即S=1+2+22+23+24+…+210=211﹣1；
（2）设S=1+3+32+33+34+…+3n，
将等式两边同时乘以3，得
3S=3+32+33+34+…+3n+1，
将下式减去上式，得
3S﹣S=3n+1﹣1
即2S=3n+1﹣1
得S=1+3+32+33+34+…+3n=．
【例】（2017秋•定远县校级期中）小聪学习了有理数后，对知识进行归纳总结．
【知识呈现】根据所学知识，完成下列填空：
（1）|﹣2|=2，|2|=2；
（2）（﹣3）2=9，32=9；
（3）若|x|=5，则x=____；
（4）若x2=4，则x=_____．
【知识归纳】根据上述知识，你能发现的结论是：_________
【知识运用】运用上述结论解答：已知|x+1|=4，（y+2）2=4，求x+y的值．
【解答】解：【知识呈现】
（3）若|x|=5，则x=±5；
（4）若x2=4，则x=±2．
【知识归纳】根据上述知识，你能发现的结论是：绝对值等于一个正数的数有两个，平方等于一个正数的数有两个；
【知识运用】根据题意得：x+1=4或﹣4，y+2=2或﹣2，
解得：x=3或﹣5，y=0或﹣4，
当x=3，y=0时，x+y=3；
当x=3，y=﹣4时，x+y=﹣1；
当x=﹣5，y=0时，x+y=﹣5；
当x=﹣5，y=﹣4时，x+y=﹣9．
综上所述，x+y的值是3，﹣1，﹣5，﹣9．．
故答案为：±5；±2；绝对值等于一个正数的数有两个，平方等于一个正数的数有两个．
总述

总结：“奇负偶正”你了解全了吗？



4有理数的混合运算
知识概述


一． 有理数混合运算顺序：
1. 先乘方，再乘除，最后加减；
2. 同级运算，从左到右进行；
3. 如有括号，先做括号内的运算，按小括号、中括号、大括号的顺序依次进行．
二． 进行有理数混合运算时的易错点：
1. 乘方概念错误，如等．
2. 底数错误，如，等．
3. 运算顺序发生错误，如等．
4. 分配律运算错误，如等．
小试牛刀


【例】（2017秋•黄埔区期末）定义新运算，若a▽b=a﹣2b，则[（3▽2）▽1]▽[2▽（3▽4）]=______．
【解答】解：根据题中的新定义得：原式=[（﹣1）▽1]▽[2▽（﹣5）]=（﹣3）▽12=﹣3﹣24=﹣27，
故答案为：﹣27
再接再厉


【例】（2017秋•南京期末）计算
（1）﹣×3+6×（﹣）
（2）（﹣1）2÷×[6﹣（﹣2）3]．
【解答】解：（1）﹣×3+6×（﹣）
=﹣1+（﹣2）
=﹣3；
（2）（﹣1）2÷×[6﹣（﹣2）3]
=1×2×[6﹣（﹣8）]
=1×2×14
=28．
【练习】（2017秋•昌平区期末）计算：（﹣+﹣）×（﹣24）．
【解答】解：原式=﹣×（﹣24）+×（﹣24）﹣×（﹣24）
=8﹣20+9
=﹣3
【巩固】（2017秋•宝丰县期末）计算：
（1）
（2）．
【解答】解：（1）原式=﹣1+2﹣16×（﹣）×，
=﹣1+2+4，
=5；
（2）原式=6×﹣6×﹣9×（﹣），
=2﹣3+，
=﹣．
【练习】（2017秋•蓬溪县期末）计算：
（1）﹣20+（﹣14）﹣（﹣18）﹣13
（2）4﹣8×（﹣）3
（3）
（4）
【解答】解：（1）原式=﹣20﹣14+18﹣13
=﹣47+18
=﹣29；
（2）原式=4﹣8×（﹣）
=4+1
=5；
（3）原式=（﹣﹣+）×36
=﹣×36﹣×36+×36
=﹣27﹣20+21
=﹣26；
（4）原式=÷﹣×16
=×﹣
=﹣
=﹣．
【练习】（2017秋•平度市期末）（1）﹣|﹣7+1|+3﹣2÷（﹣）
（2）（）÷（﹣）×
（3）
【解答】解：（1）原式=﹣6+3+6=3；
（2）原式=﹣×（﹣）×=1；
（3）原式===2.2．
【巩固】（2017秋•福田区期末）计算：
（1）16﹣（﹣18）+（﹣9）﹣15
（2）（﹣+﹣）×24﹣
（3）﹣32+（﹣2）2×（﹣5）﹣|﹣6|
【解答】解：（1）16﹣（﹣18）+（﹣9）﹣15
=16+18﹣9﹣15
=10；
（2）（﹣+﹣）×24﹣
=﹣4+14﹣9﹣
=；
（3）﹣32+（﹣2）2×（﹣5）﹣|﹣6|
=﹣9+4×（﹣5）﹣6
=﹣9﹣20﹣6
=﹣35．
综合练习
一．选择题（共4小题）
1．3x﹣12的值与互为倒数，则x的值为（　　）
A．3 B．﹣3 C．5 D．﹣5
【解答】解：∵代数式3x﹣12的值与﹣互为倒数，
∴（3x﹣12）×（﹣）＝1，即﹣x+4＝1，
解得，x＝3．
故选：A．
2．若“！”是一种数学运算符号，并且1！＝1，2！＝2×1＝2，3！＝3×2×1＝6，4！＝4×3×2×1，…，则的值为（　　）
A． B．49！ C．2450 D．2！
【解答】解：＝＝50×49＝2450
故选：C．
3．对于有理数a、b，如果ab＜0，a+b＜0．则下列各式成立的是（　　）
A．a＜0，b＜0 B．a＞0，b＜0且|b|＜a
C．a＜0，b＞0且|a|＜b D．a＞0，b＜0且|b|＞a
【解答】解：∵ab＜0，
∴a，b异号．
∵a+b＜0，
∴a、b同负或异号，且负数的绝对值较大．
综上所述，知a、b异号，且负数的绝对值较大．
故选：D．
4．若a＝﹣0.1，则a，从小到大的顺序是（　　）
A． B． C． D．
【解答】解：∵a＝﹣0.1，
∴，
∴，
故选：C．
5．据统计，2018年中国粮食总产量达到657900000吨，数657900000用科学记数法表示为（　　）
A．6.579×107 B．6.579×108 C．6.579×109 D．6.579×1010
【解答】解：将657 900 000用科学记数法表示为：6.579×108．
故选：B．
6．近似数5.10精确到（　　）
A．个位 B．十分位 C．百分位 D．十位
【解答】解：近似数5.10精确到百分位．
故选：C．
二．填空题（共2小题）
1．计算﹣4÷×（﹣2）＝　32　．
【解答】解：原式＝﹣16×（﹣2）＝32，
故答案为：32．
2．已知|x|＝3，|y|＝．且xy＜0，则的值等于　﹣15　．
【解答】解：∵|x|＝3，|y|＝．且xy＜0，
∴x＝3，y＝﹣或x＝﹣3，y＝，
所以，
故答案为：﹣15
三．解答题（共2小题）
1．计算：
【解答】解：原式＝××＝．
2．计算：（）×24．
【解答】解：原式＝×24+×24﹣×24
＝3+16﹣18
＝19﹣18
＝1．
3．计算：
（1）1÷（﹣）2﹣|﹣|×（﹣2）3×（﹣1）
（2）﹣12016+[×（﹣+）×（﹣12）+16]
【解答】解：（1）原式＝1×9﹣×（﹣8）×（﹣1）
＝9﹣4
＝5；

（2）原式＝﹣1+（﹣+）×（﹣12）+16×
＝﹣1﹣4+3﹣2+14
＝﹣7+17
＝10．
4．计算：﹣22﹣[﹣5+15×÷（﹣3）2]
【解答】解：﹣22﹣[﹣5+15×÷（﹣3）2]
＝﹣4﹣（﹣5+15×÷9）
＝﹣4﹣（﹣5+9÷9）
＝﹣4﹣（﹣5+1）
＝﹣4+4
＝0．
5．计算：
（1）
（2）﹣24﹣（﹣2）3÷
【解答】解：（1）原式＝8﹣6+20＝22；
（2）原式＝﹣16﹣（﹣8）××9＝﹣16﹣（﹣27）＝﹣16+27＝11．
6．计算：
（1）（+﹣）×（﹣48）
（2）（﹣5）3×（﹣）+32÷（﹣2）2×
【解答】解：（1）（+﹣）×（﹣48）
＝×（﹣48）+×（﹣48）﹣×（﹣48）
＝﹣40﹣42+46
＝﹣36；
（2）（﹣5）3×（﹣）+32÷（﹣2）2×
＝（﹣125）×（﹣）+32÷4×
＝75+8×
＝75﹣10
＝65．