初中数学人教版八年级上册11.3.1 多边形精品ppt课件

这是一份初中数学人教版八年级上册11.3.1 多边形精品ppt课件，文件包含《多边形及其内角和》课件pptx、2022年人教版数学八年级上册《多边形及其内角和》同步练习docx、2022年人教版数学八年级上册《多边形及其内角和》教学设计docx等3份课件配套教学资源，其中PPT共23页， 欢迎下载使用。

1. 掌握多边形的概念.2. 学会运用多边形内角和、外角和公式.
观察以下图片，你能找出哪几种图形呢？
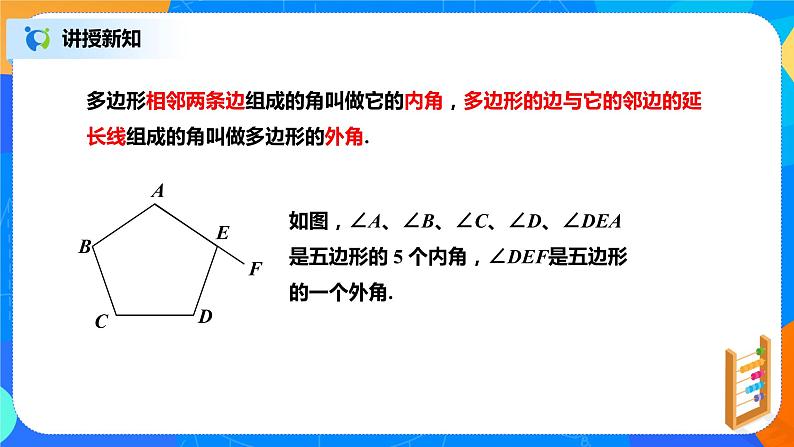
多边形相邻两条边组成的角叫做它的内角，多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
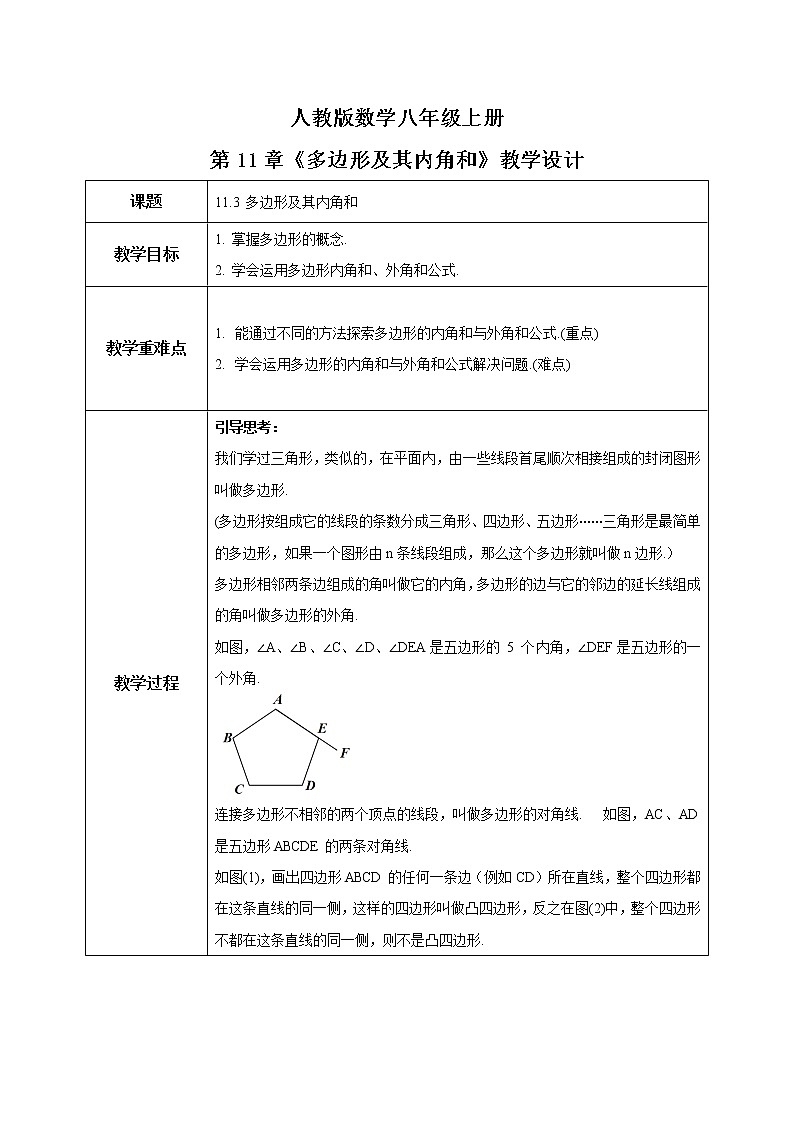
如图，∠A、∠B、∠C、∠D、∠DEA是五边形的 5 个内角，∠DEF是五边形的一个外角.
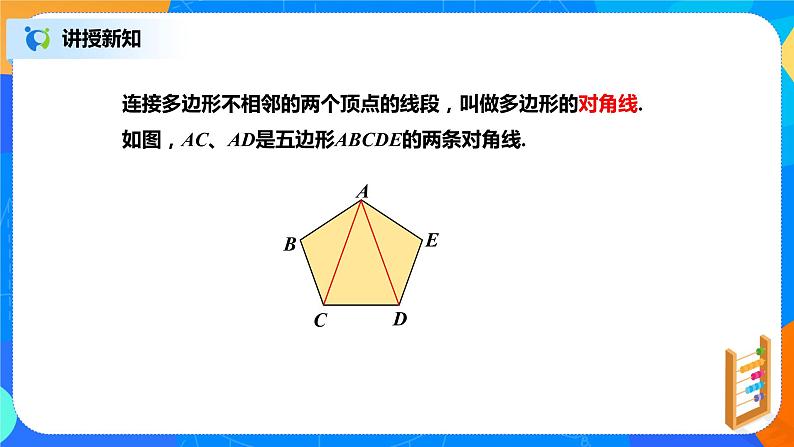
连接多边形不相邻的两个顶点的线段，叫做多边形的对角线. 如图，AC、AD是五边形ABCDE的两条对角线.
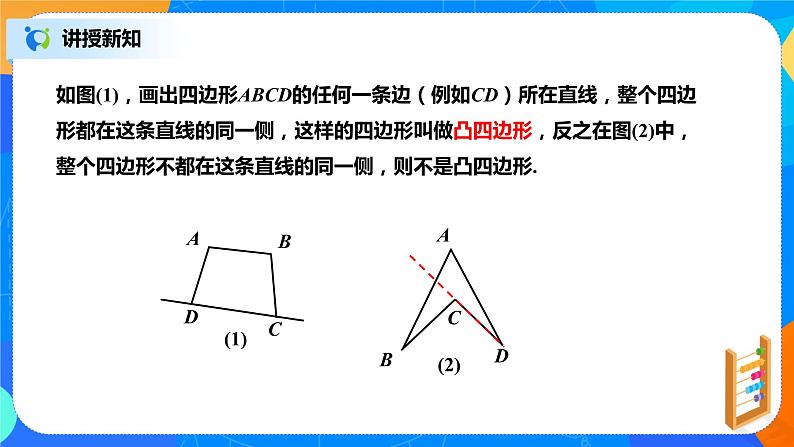
如图(1)，画出四边形ABCD的任何一条边（例如CD）所在直线，整个四边形都在这条直线的同一侧，这样的四边形叫做凸四边形，反之在图(2)中，整个四边形不都在这条直线的同一侧，则不是凸四边形.
类似的，画出多边形的任何一条边所在直线，如果整个多边形都在这条直线的同一侧，那么这个多边形就是凸多边形，本节只讨论凸多边形.
像正方形这样，各个角都相等，各条边都相等的多边形叫做正多边形. 如正三角形、正方形、正五边形等.
我们知道，三角形的内角和等于180°，正方形、长方形的内角和都等于360°，那么，任意一个四边形的内角和是否也等于360°呢？你能利用三角形内角和定理证明四边形的内角和等于360°吗？
如图，在四边形ABCD中，连接对角线BD，则四边形ABCD被分为△ABD和△BCD两个三角形.由此可得∠A +∠ABC +∠C +∠ADC=∠A +∠1 +∠2 +∠C +∠4 +∠3=(∠1 +∠A +∠3)+(∠2 +∠C +∠4)∵∠1 +∠A +∠3=180°， ∠2 +∠C +∠4=180°，∴∠A +∠ABC +∠C +∠ADC =180°+180°=360°.即四边形的内角和等于360°.
类比上题的过程，你能推导出五边形和六边形的内角和是多少吗？观察图形并填空.从五边形的一个顶点出发，可以作_____条对角线，它们将五边形分成_____个三角形，五边形的内角和等于180°×______.从六边形的一个顶点出发，可以作_____条对角线，它们将六边形分成_____个三角形，六边形的内角和等于180°×______.
通过以上过程，你能发现多边形的内角和与边数的关系吗？
一般的，从 n边形的一个顶点出发，可以作 条对角线，它们将 n边形分为 个三角形，n边形的内角和等于 .
这样我们就得出了多边形内角和公式： .
例1 如果一个四边形的一组对角互补，那么另一组对角有什么关系？
例2 如图，在六边形的每个顶点各取一个外角，这些外角的和叫做六边形的外角和，六边形的外角和等于多少？
分析：思考以下问题：(1) 任意一个外角与它相邻的内角有什么数量关系？
答：任意一个外角与它相邻的内角和为180°.
(2) 六边形的六个外角加上与它们相邻的内角，所得的总和是多少？
答：一个外角加上与之相邻的内角和为180°，六个外角加上与它们相邻的内角所得的总和为180°×6.
(3) 上述总和与六边形的内角和、外角和有什么关系？
联系这些问题，考虑外角和的求法.
1. 求出下列图形中 x 的值.
2. (1) 一个多边形的内角和是外角和的一半，它是几边形？
2. (2) 一个多边形的内角和是外角和的 2 倍，它是几边形？
3. 如图，六边形 ABCDEF 的内角都相等，∠DAB=60°，AB 与 DE 有怎样的位置关系？BC 与 EF 有这种关系吗？这些结论是怎样得出的？