湘教版（2019）必修 第一册5.3 三角函数的图象与性质优秀教案设计

5．3.2　正切函数的图象与性质

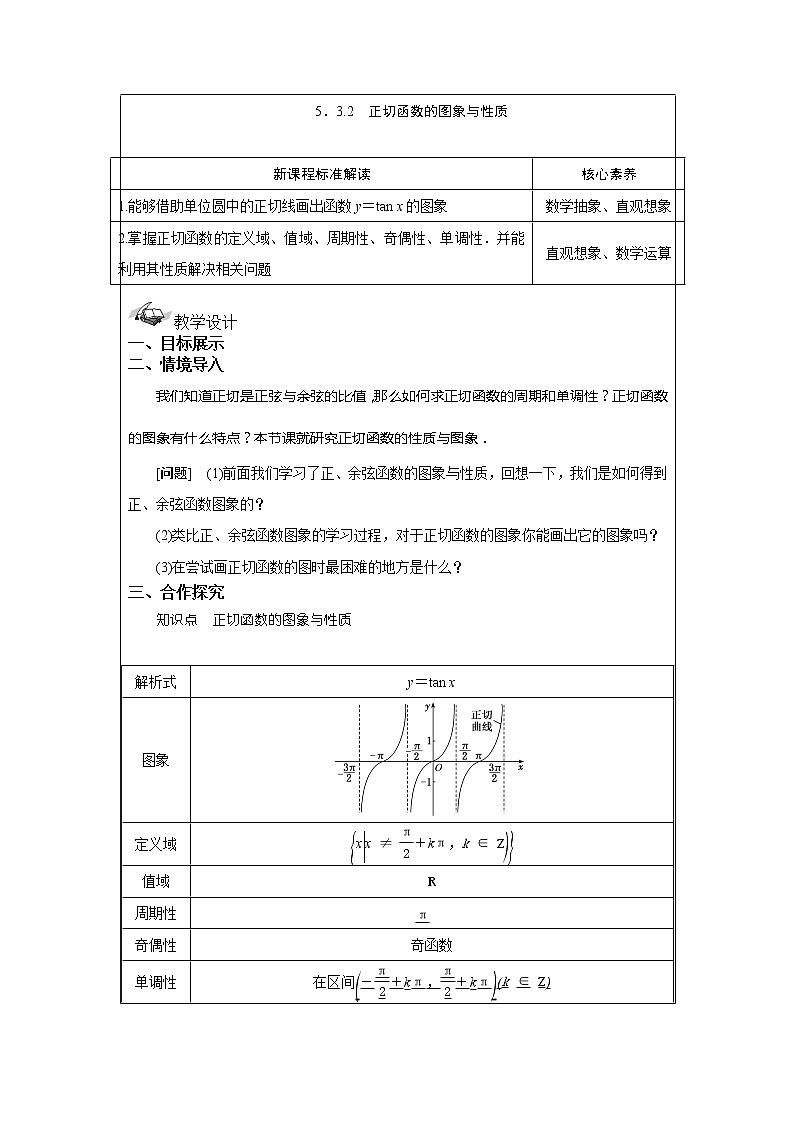
教学设计

一、目标展示

二、情境导入

我们知道正切是正弦与余弦的比值，那么如何求正切函数的周期和单调性？正切函数的图象有什么特点？本节课就研究正切函数的性质与图象．

[问题]　(1)前面我们学习了正、余弦函数的图象与性质，回想一下，我们是如何得到正、余弦函数图象的？

(2)类比正、余弦函数图象的学习过程，对于正切函数的图象你能画出它的图象吗？

(3)在尝试画正切函数的图时最困难的地方是什么？

三、合作探究

知识点　正切函数的图象与性质

四、精讲点拨

[例1]　(链接教科书第180页例5)(1)函数y＝的定义域为(　　)

A.，k∈Z

B.，k∈Z

C.，k∈Z

D.，k∈Z

(2)函数y＝tan2x－2tan x＋3的最小值为________．

[例2]　(链接教科书第182页习题10题)(1)若f(x)＝tan ωx(ω>0)的周期为1，则f的值为(　　)

A．－　　　　　　　 B．－

C.  D．

(2)已知函数f(x)＝tan x＋，若f(a)＝5，则f(－a)＝________．

[例3]　(1)比较大小：tan和tan；

(2)求函数y＝tan的单调区间．

五、达标检测

1．函数y＝的定义域为(　　)

A.(k∈Z)          B.(k∈Z)

C.(k∈Z)          D.(k∈Z)

2．已知函数f(x)＝3tan的最小正周期为，则正数ω＝(　　)

A．4  B．3

C．2  D．1

3．求函数y＝tan，x∈的值域．

六、课堂小结

   1. 正切函数的定义域及值域;

   2. 正切函数的周期性、奇偶性;

   3. 正切函数的单调性及应用.

课后作业

教后反思