









苏教版 (2019)5.3 导数在研究函数中的应用说课课件ppt
展开1.能利用导数求某些函数在给定闭区间上的最大值、最小值.2.体会导数与函数单调性、极值、最大(小)值的关系.
通过解决函数的最大(小)值问题,提升学生的数学运算和直观想象素养.
问题导学预习教材必备知识探究
互动合作研析题型关键能力提升
拓展延伸分层精练核心素养达成
WEN TI DAO XUE YU XI JIAO CAI BI BEI ZHI SHI TAN JIU
问题导学预习教材 必备知识探究
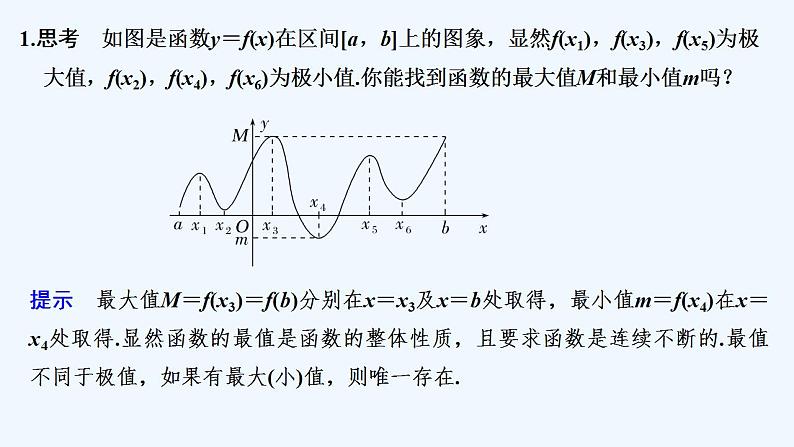
1.思考 如图是函数y=f(x)在区间[a,b]上的图象,显然f(x1),f(x3),f(x5)为极大值,f(x2),f(x4),f(x6)为极小值.你能找到函数的最大值M和最小值m吗?
提示 最大值M=f(x3)=f(b)分别在x=x3及x=b处取得,最小值m=f(x4)在x=x4处取得.显然函数的最值是函数的整体性质,且要求函数是连续不断的.最值不同于极值,如果有最大(小)值,则唯一存在.
2.填空 (1)如果在函数定义域I内存在x0,使得对任意的x∈I,总有f(x)____ f(x0),那么称f(x0)为函数f(x)在定义域上的最大值.(2)如果在函数定义域I内存在x0,使得对任意的x∈I,总有f(x)____ f(x0),那么称f(x0)为函数f(x)在定义域上的最小值.函数的最大(小)值是相对函数定义域整体而言的,如果存在最大(小)值,那么函数的最大(小)值______.
温馨提醒 (1)函数的极值不一定是最值,需要将极值和区间端点的函数值进行比较,或者考查函数在区间内的单调性.(2)如果连续函数在区间(a,b)内只有一个极值,那么极大值就是最大值,极小值就是最小值.
HU DONG HE ZUO YAN XI TI XING GUAN JIAN MENG LI TI SHENG
互动合作研析题型 关键能力提升
例1 求下列各函数的最值. (1)f(x)=x3-3x2+6x-2,x∈[-1,1];
解 f′(x)=3x2-6x+6=3(x2-2x+2)=3(x-1)2+3,∵f′(x)在[-1,1]内恒大于0,∴f(x)在[-1,1]上为增函数.故当x=-1时,f(x)min=-12;当x=1时,f(x)max=2.
(2)f(x)=x+sin x,x∈[0,2π].
求可导函数f(x)在区间[a,b]上的最大值与最小值的步骤(1)求f(x)在区间(a,b)上的极值;(2)将第一步中求得的极值与f(a),f(b)比较,得到f(x)在区间[a,b]上的最大值与最小值.
训练1 求下列函数的最值: (1)f(x)=2x3-6x2+3,x∈[-2,4];
解 f′(x)=6x2-12x=6x(x-2).令f′(x)=0,得x=0或x=2.当x变化时,f′(x),f(x)的变化情况如下表
∴当x=4时,f(x)取最大值35.当x=-2时,f(x)取最小值-37.
(2)f(x)=e-x-ex,x∈[0,a],a为正实数.
当x∈[0,a]时,f′(x)<0恒成立,所以f(x)在[0,a]上是减函数.故当x=a时,f(x)有最小值f(a)=e-a-ea;当x=0时,f(x)有最大值f(0)=e-0-e0=0.
例2 已知函数f(x)=x3-ax2-a2x.求函数f(x)在[0,+∞)上的最小值.
题型二 含参数的函数的最值问题
①当a>0时,f(x)在[0,a)上是减函数,在[a,+∞)上是增函数,所以f(x)min=f(a)=-a3.②当a=0时,f′(x)=3x2≥0,f(x)在[0,+∞)上是增函数,所以f(x)min=f(0)=0.
迁移 当a>0时,求函数f(x)=x3-ax2-a2x在[-a,2a]上的最值.
含参数的函数最值问题的两类情况(1)能根据条件求出参数,从而化为不含参数的函数的最值问题.(2)对于不能求出参数值的问题,则要对参数进行讨论,其实质是讨论导函数大于0、等于0、小于0三种情况.若导函数恒不等于0,则函数在已知区间上是单调函数,最值在端点处取得;若导函数可能等于0,则求出极值点后求极值,再与端点值比较后确定最值.
训练2 已知a∈R,函数f(x)=x2(x-a),求f(x)在区间[0,2]上的最大值.
题型三 由函数的最值求参数问题
例3 已知函数f(x)=ax3-6ax2+b,x∈[-1,2]时,f(x)的最大值为3,最小值为-29,求a,b的值.
解 由题设知a≠0,否则f(x)=b为常数,与题设矛盾.f′(x)=3ax2-12ax=3ax(x-4),x∈[-1,2].令f′(x)=0,得x1=0,x2=4(舍去).(1)当a>0时,当x变化时,f′(x),f(x)的变化情况如下表:
由表可知,当x=0时,f(x)取得最大值.∴f(0)=3,即b=3.又f(-1)=-7a+3,f(2)=-16a+3
由函数的最值来确定参数的值或取值范围是利用导数求函数的最值问题的逆向运用,这类问题的解题步骤为:(1)求导数f′(x),并求极值;(2)利用单调性,将极值与端点处的函数值进行比较,确定函数的最值,若参数的变化影响着函数的单调性,则要对参数进行分类讨论;(3)利用最值列出关于参数的方程(组),解方程(组)即可.
训练3 已知函数h(x)=x3+3x2-9x+1在区间[k,2]上的最大值是28,求实数k的取值范围.
解 ∵h(x)=x3+3x2-9x+1,∴h′(x)=3x2+6x-9.令h′(x)=0,得x1=-3,x2=1,当x变化时,h′(x),h(x)的变化情况如下表:
当x=-3时,f(x)取极大值28;当x=1时,f(x)取极小值-4.而h(2)=3
TUO ZHAN YAN SHEN FEN CENG JING LIAN HE XING SU YANG DA CHENG
拓展延伸分层精练 核心素养达成
1.已知函数f(x),g(x)均为[a,b]上的可导函数,在[a,b]上连续且f′(x)
解析 ∵f′(x)=3x2-3a,令f′(x)=0,可得a=x2,又∵x∈(0,1),∴0
5.已知函数f(x)=ex-x+a,若f(x)>0恒成立,则实数a的取值范围是( )A.(-1,+∞) B.(-∞,-1)C.[-1,+∞) D.(-∞,-1]
解析 f′(x)=ex-1,令f′(x)>0,解得x>0,令f′(x)<0,解得x<0,故f(x)在(-∞,0)上是减函数,在(0,+∞)上是增函数,故f(x)min=f(0)=1+a.若f(x)>0恒成立,则1+a>0,解得a>-1,故选A.
7.已知函数f(x)=-x2+mx+1在区间(-2,-1)上的最大值就是函数f(x)的极大值,则实数m的取值范围是__________.
解析 ∵f′(x)=-2x2+4ax+3=-2(x-a)2+3+2a2,∴f′(x)max=3+2a2=5.∵a>0,∴a=1.
10.已知函数f(x)=2ex(x+1). (1)求函数f(x)的极值;
解 f(x)的定义域为R,f′(x)=2ex(x+2),由f′(x)>0,得x>-2;由f′(x)<0,得x<-2.∴f(x)在(-2,+∞)上单调递增,在(-∞,-2)上单调递减.∴f(x)的极小值为f(-2)=-2e-2,无极大值.
(2)求函数f(x)在区间[t,t+1](t>-3)上的最小值.
解 由(1),知f(x)在(-2,+∞)上单调递增,在(-∞,-2)上单调递减.∵t>-3,∴t+1>-2.①当-3
∵a<0,∴f′(x)>0,故函数在其定义域(0,+∞)上单调递增.∴f(x)的单调增区间为(0,+∞),无单调减区间.
苏教版 (2019)第5章 导数及其应用5.3 导数在研究函数中的应用习题课件ppt: 这是一份苏教版 (2019)第5章 导数及其应用5.3 导数在研究函数中的应用习题课件ppt,共60页。PPT课件主要包含了求含参数的函数的最值,反思感悟,随堂演练,课时对点练,-71,因为x∈01,解得a=1等内容,欢迎下载使用。
高中数学苏教版 (2019)必修 第一册3.3 从函数观点看一元二次方程和一元二次不等式多媒体教学课件ppt: 这是一份高中数学苏教版 (2019)必修 第一册3.3 从函数观点看一元二次方程和一元二次不等式多媒体教学课件ppt,文件包含第二课时函数的最大小值pptx、第二课时函数的最大小值doc等2份课件配套教学资源,其中PPT共47页, 欢迎下载使用。
【最新版】高中数学(新人教B版)习题+同步课件限时小练21 函数的最大(小)值: 这是一份【最新版】高中数学(新人教B版)习题+同步课件限时小练21 函数的最大(小)值,文件包含限时小练21函数的最大小值pptx、限时小练21函数的最大小值doc等2份课件配套教学资源,其中PPT共6页, 欢迎下载使用。













