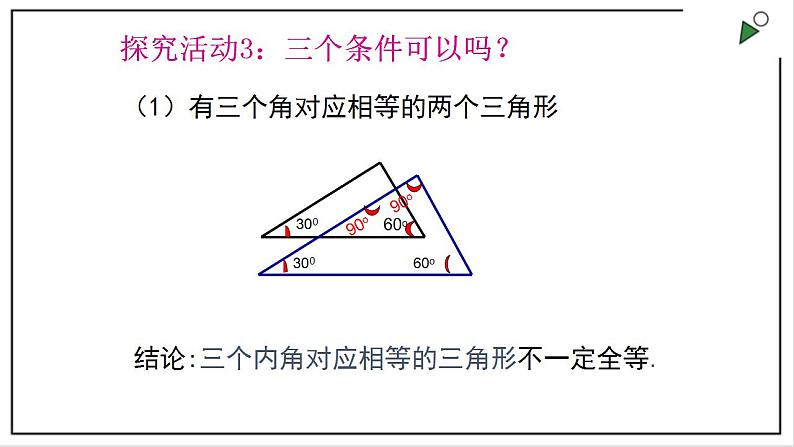
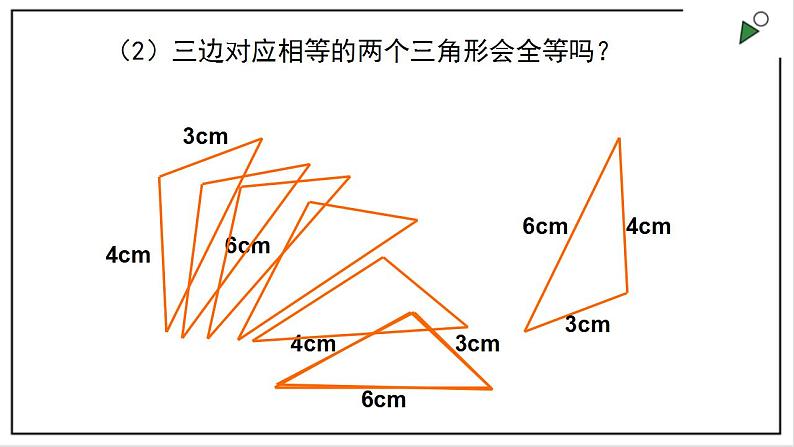
苏科版八年级上册1.3 探索三角形全等的条件优秀ppt课件

1.3.1探索三角形全等的条件

一、单选题

1．下列判断中错误的是（　　）

A．有两角和一边对应相等的两个三角形全等

B．有两边和一角对应相等的两个三角形全等

C．有两边和其中一边上的中线对应相等的两个三角形全等

D．有一边对应相等的两个等边三角形全等

2．如图，在△ABC与△ADC中，若，则下列条件不能判定△ABC与△ADC全等的是(     )

A． B． C． D．

3．某同学把一块三角形的玻璃打碎成了3块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的方法是（       ）．

A．带①去 B．带②去 C．带③去 D．①②③都带

4．如图，，点D、E分别在AB、AC上，补充一个条件后，仍不能判定△ABE与△ACD全等的是（       ）

A． B．

C． D．

5．如图，已知，下面甲、乙、丙、丁四个三角形中，与全等的是（       ）

A．甲 B．乙 C．丙 D．丁

6．在下列各组的三个条件中，能判定△ABC和△DEF全等的是（        ）

A．AC=DF，BC=DE，∠B=∠D B．∠A=∠F，∠B=∠E，∠C=∠D

C．AB=DF，∠B=∠E，∠C=∠F D．AB=EF，∠A =∠E，∠B=∠F

7．如图，在和中，已知，添加两个条件仍不能使的是（       ）

A．， B．，

C．， D．，

8．根据下列已知条件，能画出唯一的△ABC的是（        ）

A．，， B．，，

C．， D．，，

9．如图，在方格纸中，以AB为一边作△ABP，使之与△ABC全等，从P1，P2，P3，P4四个点中找出符合条件的点P，则点P有（ ）

A．1个 B．2个 C．3个 D．4个

10．如图，在△ABC与△AEF中，AB＝AE，BC＝EF，∠ABC＝∠AEF，∠EAB＝40°，AB交EF于点D，连接EB．下列结论：①∠FAC＝40°；②AF＝AC；③∠EBC＝110°；④AD＝AC；⑤∠EFB＝40°，正确的个数为（       ）个．

A．1 B．2 C．3 D．4

二、填空题

11．三角形全等的判定方法——“角边角”（即ASA）指的是_______________________________

12．如图，∠1=∠2，要使△ABE≌△ACE，需添加一个条件是__________．（填上一个条件即可）

13．如图，点D是△ABC的边AB上一点，FC∥AB，连接DF交AC于点E，若CE=AE，AB=7，CF=4，则BD的长为________．

14．工人师傅常用角尺平分一个任意角．做法如下：如图，∠AOB 是一个任意角，在边 OA，OB 上分别取OM=ON，移动角尺，使角尺两边相同的刻度分别与点 M，N 重合，过角尺顶点C 作射线 OC．由此做法得 △MOC≌△NOC 的依据是____．

15．在与中，，那么______．

16．如图，填空：（填、、或

（1）已知，，利用__可以判定；

（2）已知，，利用___可以判定；

（3）已知，，利用___可以判定；

（4）已知，，利用___可以判定．

17．如图是由九个边长为1的小正方形拼成的大正方形，图中∠1＋∠2＋∠3＋∠4＋∠5的度数为______．

18．如图，BE交AC于点M，交CF于点D，AB交CF于点N，，给出的下列五个结论中正确结论的序号为                             ．

①；②；③；④；⑤．

三、解答题

19．如图，点B，F，C，E在同一条直线上，BF＝EC，AB＝DE，∠B＝∠E．求证：∠A＝∠D．

20．如图，，点E在BC上，且，．

(1)求证：；

(2)判断AC和BD的位置关系，并说明理由．

21．如图，在△ABC中，点D是BC的中点，E是AB边上一点，过点C作CF∥AB交ED的延长线于点F．求证：△BDE≌△CDF．

22．已知：如图，，，．求证：．

23．如图，AB=AC，BE⊥AC于E，CD⊥AB于D，求证：BD=CE．

请补全下列的证明过程

证明：∵BE⊥AC，CD⊥AB，

∴∠AEB=90°，∠ADC=90°，

∴          ，

∵在△AEB和△ADC中，

，

∴△AEB≌△ADC（    ），

∴AE=AD，

∴AB-AD=AC-   ，

即BD=CE，

24．请将以下推导过程补充完整．

如图，点在线段上，，，，平分．

求证：．

证明：∵

∴

在和中

∴（________）

∴（___________）

∵平分

∴________

在和中

∴

25．如图，在中，D是BC的中点，过点D的直线GF交AC于点F，交AC的平行线BG于点G，交AB于点E，连接EG、EF．

（1）求证：．

（2）请你判断：与EF的大小关系，并加以证明．

26．如图，在四边形中，，，垂足为点，是的中点，连结并延长交的延长线于点.

(1)图中可以由______绕着点______旋转______度后得到；

(2)写出图中的一对全等三角形______；

(3)若，，，求的面积.

27．如图：在△ABC中，∠C=90°，AC=BC，过点C在△ABC外作直线MN，AM⊥MN于M，BN⊥MN于N．

(1)MN=AM+BN成立吗？为什么？

 (2)若过点C在△ABC内作直线MN，AM⊥MN于M，BN⊥MN于N，则AM、BN与MN之间有什么关系？请说明理由．

28．（1）如图1，∠MAN=90°，射线AE在这个角的内部，点B、C在∠MAN的边AM，AN上，且AB=AC，CF⊥AE于点F，BD⊥AE于点D．求证：．

（2）如图2，点B、C在∠MAN的边AM、AN上，点E、F在∠MAN内部射线AD上，∠1，∠2分别是，的外角，已知AB=AC，∠1=∠2=∠BAC，求证：；

（3）如图3，在中，AB=AC，AB>BC，点D在边BC上，CD=2BD，点E、F在线段AD上，，若的面积是15，则与的面积之和是_________．