高中数学人教B版 (2019)必修 第一册1.2.3 充分条件、必要条件教学ppt课件

这是一份高中数学人教B版 (2019)必修 第一册1.2.3 充分条件、必要条件教学ppt课件，共27页。PPT课件主要包含了新知探究，充分条件与必要条件，充分条件，必要条件，拓展深化微判断，微训练，微思考，素养落地，素养训练，答案C等内容，欢迎下载使用。

某居民的卧室里安有一盏灯，在卧室门口和床头各有一个开关，任意一个开关都能够独立控制这盏灯.这就是电器上常用的“双刀”开关，如图所示.问题　(1)A开关闭合时B灯一定亮吗？(2)B灯亮时A开关一定闭合吗？提示　(1)一定亮.(2)不一定，还可能是C开关闭合.
区分概念中充分条件与必要条件的推出方向
(2)用集合知识理解充分条件与必要条件一般地，如果A＝{x|p(x)}，B＝{x|q(x)}，且A⊆B(如图所示)，那么p(x)⇒q(x)，因此也就有p(x)是q(x)的____________，q(x)是p(x)的____________.
(3)充分条件、必要条件与判定定理、性质定理的关系①判定定理实际上是给出了一个充分条件；②性质定理实际上是给出了一个必要条件.
1.若p是q的充分条件，则p是唯一的.( )提示　不是唯一的，使结论成立的条件有多个.2.“若q，则p”是真命题，则p是q的必要条件.( )3.“x＝3”是“x2＝9”的充分条件.( )4.“ab>0”是“a>0，b>0”的必要条件.( )
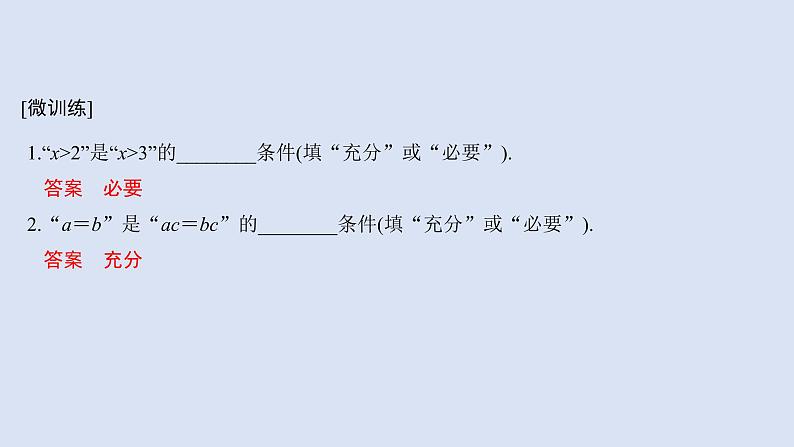
1.“x>2”是“x>3”的________条件(填“充分”或“必要”).答案　必要2.“a＝b”是“ac＝bc”的________条件(填“充分”或“必要”).答案　充分
你能将性质定理“菱形的对角线互相垂直”写成“若p，则q”的形式，并用必要条件的语言表述吗？提示　“菱形的对角线互相垂直”可表述为“若四边形为菱形，则这个四边形的对角线互相垂直”，所以“对角线互相垂直”是“四边形为菱形”的必要条件.
题型一　充分条件的判断【例1】　判断下列各题中，p是否是q的充分条件：
解　(1)由于QR，所以p⇒q，所以p是q的充分条件.
(3)由x>1可以推出x2>1.因此p⇒q，所以p是q的充分条件.
(5)由三角形中大角对大边可知，若∠A>∠B，则BC>AC.因此，p⇒q，所以p是q的充分条件.
规律方法　充分条件的判断方法第一步：确定谁是条件，谁是结论；第二步：尝试由条件推结论；第三步：若条件能推出结论，则条件为结论的充分条件，否则条件就不是结论的充分条件.
【训练1】　判断下列各题中，p是否是q的充分条件：
(1)p：x2＝y2，q：x＝y；(2)p：一元二次方程ax2＋bx＋c＝0有实数根，q：b2－4ac≥0；(3)p：整数a能被4整除；q：整数a的个位数字为偶数；(4)p：(x－1)2＋(y－2)2＝0，q：(x－1)(y－2)＝0.
(2)若一元二次方程有实数根，则根的判别式大于等于0，即b2－4ac≥0，所以p⇒q，所以p是q的充分条件.(3)若整数a能被4整除，则a是偶数，所以a的个位数字为偶数，所以p⇒q，所以p是q的充分条件.(4)因为(x－1)2＋(y－2)2＝0⇒x＝1且y＝2⇒(x－1)(y－2)＝0，所以p⇒q，所以p是q的充分条件.
题型二　必要条件的判断【例2】　判断下列各题中，q是否是p的必要条件：
规律方法　必要条件的判断方法第一步：确定谁是条件，谁是结论；第二步：尝试由条件推结论：第三步：若条件能推出结论，则结论为条件的必要条件，否则结论就不是条件的必要条件.
【训练2】　判断下列各题中，q是否是p的必要条件：
(1)p：a是1的平方根，q：a＝1；(2)p：4x2－mx＋9是完全平方式，q：m＝12；(3)p：a是无理数，q：a是无限小数；(4)p：a与b互为相反数，q：a与b的绝对值相等.
(3)因为无理数是无限不循环小数，所以p⇒q，所以q是p的必要条件.(4)若a与b互为相反数，则a与b的绝对值相等，所以p⇒q，所以q是p的必要条件.
题型三　充分条件与必要条件的应用【例3】　已知p：实数x满足3a解　p：3a【迁移1】　将本例中条件p改为“实数x满足a0”，若p是q的必要条件，求实数a的取值范围.
解　p：a0}.q：－2≤x≤3，即集合B＝{x|－2≤x≤3}.
【迁移2】　将例题中的条件“q：实数x满足－2≤x≤3”改为“q：实数x满足 －3≤x≤0”，其他条件不变，求实数a的取值范围.
解　p：3a所以a的取值范围是[－1，0).
规律方法　充分条件与必要条件的应用技巧(1)应用：可利用充分性与必要性进行相关问题的求解，特别是求参数的值或取值范围问题.(2)求解步骤：先把p，q等价转化，利用充分条件、必要条件与集合间的包含关系，建立关于参数的不等式(组)进行求解.
【训练3】　(1)若“x2或x<1”的充分条件，求m的取值范围；
(2)已知p：x<－3或x>1，q：x>a，且p是q的必要条件，求a的取值范围.解　(1)由已知条件知{x|x2或x<1}，∴m≤1.即m的取值范围为(－∞，1].(2)由已知条件得{x|x>a}⊆{x|x<－3或x>1}，∴a≥1.即a的取值范围为[1，＋∞).
1.通过学习充分条件与必要条件的概念提升数学抽象素养，通过判断充分条件与必要条件及其应用培养逻辑推理素养.2.充分条件、必要条件的判断方法
(1)定义法：直接利用定义进行判断.(2)利用集合间的包含关系进行判断.
3.根据充分条件、必要条件求参数的取值范围时，注意转化与化归思想的应用.
1.“－21或x<－1”的(　　)
A.充分条件但不是必要条件B.必要条件但不是充分条件C.既不充分，也不必要条件D.既充分，也必要条件
2.“a>b”是“a>|b|”的(　　)
A.充分条件但不是必要条件B.必要条件但不是充分条件C.既充分也必要条件D.既不充分也不必要条件解析　由a>|b|⇒a>b，而由a>b推不出a>|b|.∴“a>b”是“a>|b|”的必要条件但不是充分条件.答案　B
3.若a∈R，则“a＝1”是“|a|＝1”的(　　)
A.充分条件但不是必要条件B.必要条件但不是充分条件C.既不充分也不必要条件D.无法判断解析　当a＝1时，|a|＝1成立，但|a|＝1时，a＝±1，∴a＝1不一定成立.∴“a＝1”是“|a|＝1”的充分条件，但不是必要条件.答案　A
4.判断下列各题中，p是q的什么条件：
(1)p：两个三角形相似，q：两个三角形全等；(2)p：一个四边形是矩形，q：四边形的对角线相等；(3)p：A⊆B，q：A∩B＝A；(4)p：a>b，q：ac>bc.