




人教版七年级下册第七章 平面直角坐标系综合与测试随堂练习题
展开专题12 《平面直角坐标系》压轴题真题分类(解析版)
第一类:坐标系中与动点有关的面积问题
1.(雅礼)如图1,在平面直角坐标系中,已知点A(﹣a,2),B(a,b),且a,b满足关系式:b=+6.
(1)求a,b的值;
(2)如图1,AB与y轴交于点C,连接OA,OB,求三角形BOC的面积及C点坐标;
(3)将线段AB向右平移8个单位得到A1B1,如图2,若点D(m,n)是线段A1B1上的动点,求m,n之间满足的数量关系.
【解答】解:(1)∵b=+6,∴,∴a=5,b=6.
(2)设C(0,m).由题意,A(﹣5,2),B(5,6),∴S△AOB=10×6﹣×2×5﹣×5×6﹣×4×10=60﹣5﹣15﹣20=20,∴•m•[5﹣(﹣5)]=20,∴m=4,∴C(0,4),∴S△BOC=×4×5=10.
(3)如图2中,过点A1作A1E⊥x轴于E,过点B1作B1F⊥x轴于F,过点A1作A1G⊥B1F于G,连接DG.由平移的性质可知,A1(3,2),B1(13,6),∵=+,
∴×10×4=×10×(n﹣2)+×4×(13﹣m),∴n=m+.
2.(青竹湖)如图所示,在平面直角坐标系中,如图①,将线段AB平移至线段CD,点A在x轴的负半轴,点C在y轴的正半轴上,连接AC、BD.
(1)若A(﹣3,0)、B(﹣2,﹣2),C(0,2),求点D的坐标;
(2)已知A(﹣3,0)、B(﹣2,﹣2),点C(0,m)在y轴的正半轴上,点D在第一象限内,且S△ACO
=5,求点C、D的坐标;
(3)如图②,在平面直角坐标系中,已知一定点M(2,0),两个动点E(a,2a+1)、F(b,﹣2b+3),请你探索是否存在以两个动点E、F为端点的线段EF平行于线段OM且等于线段OM.若存在,求以点O、M、E、F为顶点的四边形的面积;若不存在,请说明理由.
【解答】解:(1)设D(x,y),∵将线段AB平移至线段CD,A(﹣3,0)、B(﹣2,﹣2),C(0,2),
∴x﹣0=﹣2﹣(﹣3),y﹣2=﹣2﹣0,∴x=1,y=0,∴D(1,0);
(2)如图1,∵A(﹣3,0),点C(0,m)在y轴的正半轴上,∴OA=3,OC=m,
∵S△ACO=5,即OA•OC=5,∴×3m=5,解得:m=,∴点C的坐标为(0,),设D(x,y),∵将线段AB平移至线段CD,∴x﹣0=﹣2﹣(﹣3),y﹣=﹣2﹣0,∴x=1,y=,∴点D的坐标为(1,);
(3)∵EF∥OM,EF=OM,O(0,0),M(2,0),∴点E与F的纵坐标相等,横坐标的差的绝对值为2,即2a+1=﹣2b+3,|a﹣b|=2,解得:a=﹣,b=或a=,b=﹣,
∴点E的坐标为(﹣,0),F的坐标为(,0)或点E的坐标为(,4),F的坐标为(﹣,4),
当E(﹣,0),F(,0)时,O、M、E、F四点均在x轴上,不能构成平行四边形,舍去;
∴E(,4),F(﹣,4);∴S▱OMEF=2×4=8.
3.(湘一、一中双语联考)在平面直角坐标系中,点B(m,n)在第一象限,m、n均为整数,且满足.
(1)求点B的坐标;
(2)将线段OB向下平移a个单位后得到线段O′B′,过点B′作B′C⊥y轴于点C,若3CO=2CO′,求a的值;
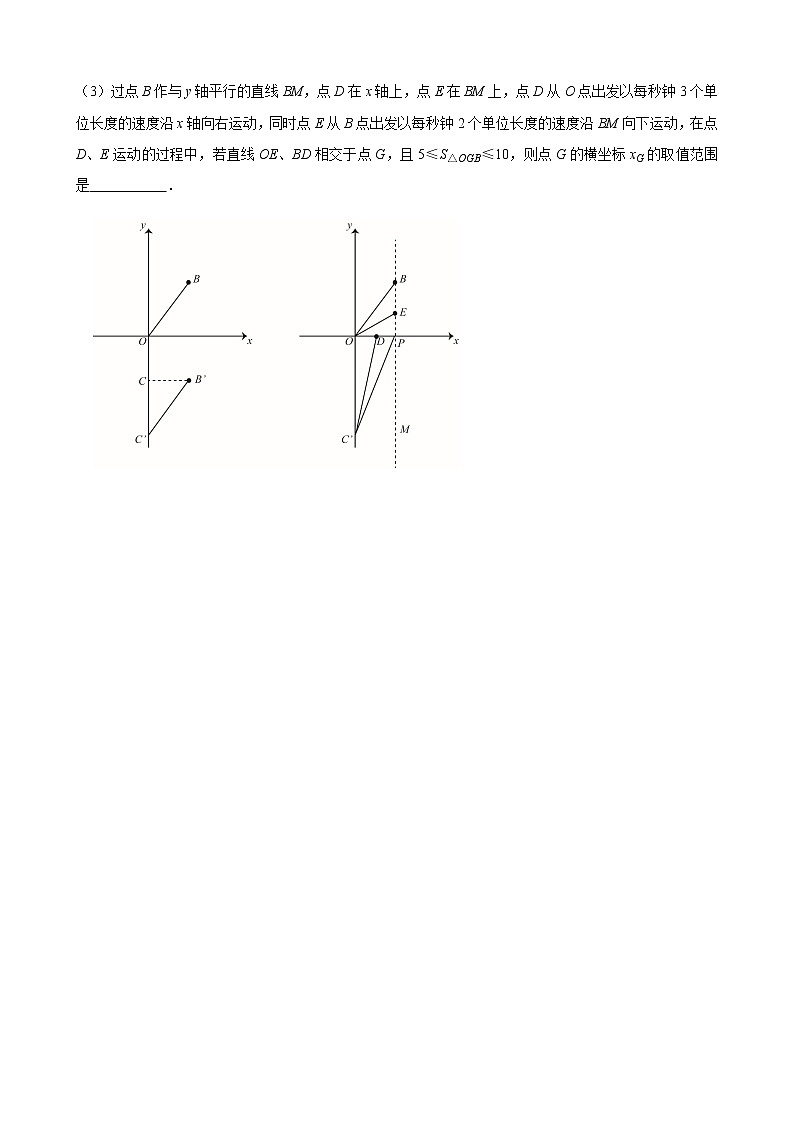
(3)过点B作与y轴平行的直线BM,点D在x轴上,点E在BM上,点D从O点出发以每秒钟3个单位长度的速度沿x轴向右运动,同时点E从B点出发以每秒钟2个单位长度的速度沿BM向下运动,在点D、E运动的过程中,若直线OE、BD相交于点G,且5≤S△OGB≤10,则点G的横坐标xG的取值范围是 .
【解答】解:(1)由题意得:,m为整数,解得:m=3或2或1,将m值代入n的等式,
解得:m=3,n=2,即点B的坐标为(3,2),
(2)平移后各点坐标如下:B′(3,2﹣a)、O′(0,﹣a)c(0,2﹣a),CO=a﹣2,CO'=2,所以3(a﹣2)=±2×2,所以a=或;
(3)①点G不可能在△OBH内,若在△OBH内,则 S△OGB<S△OBH=1/2×3×2=3<5;
②G点位置在△OBH外部时,当点G作y轴右侧时,
过点G分别作x、y轴的垂线于点K、N,设GN=c,ON=d,运动时间为t,
S△OGB=S梯形BFNG﹣S△OBF﹣S△OGN=(3+c)(2+d)﹣3﹣cd=d+c…①,
S△OGB=BE×NG=×2tc=tc…②,S△OGB=×OD×FN=×3t×(d+2)=td+3t…③,
联立①②③并解得:c=S△OGB+,∵5≤S△OGB≤10,解得:4≤c≤故答案为:4≤xG≤;
当点G作y轴左侧时,同理可得:﹣≤xG≤﹣1;故答案为:4≤xG≤或﹣≤xG≤﹣1.
第2类:坐标系中与动点有关的角度问题
4. (中雅)如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(﹣3,2).
(1)直接写出点E的坐标 ;
(2)在四边形ABCD中,点P从点B出发,沿“BC→CD”移动.若点P的速度为每秒1个单位长度,运动时间为t秒,回答下列问题:
①当t= 秒时,点P的横坐标与纵坐标互为相反数;
②求点P在运动过程中的坐标,(用含t的式子表示,写出过程);
③当3<t<5时,设∠CBP=x°,∠PAD=y°,∠BPA=z°,用含x,y的式子表示z= .
【解答】解:(1)根据题意,可得三角形OAB沿x轴负方向平移3个单位得到三角形DEC,
∵点A的坐标是(1,0),∴点E的坐标是(﹣2,0);故答案为:(﹣2,0);
(2)①∵点C的坐标为(﹣3,2)∴BC=3,CD=2,∵点P的横坐标与纵坐标互为相反数;
∴点P在线段BC上,∴PB=CD,即t=2;∴当t=2秒时,点P的横坐标与纵坐标互为相反数;
故答案为:2;
②当点P在线段BC上时,∵BC∥x轴,且点B(0,2),∴点P的坐标(﹣t,2),当点P在线段CD上时,∵BC=3,CD=2,∴点P的纵坐标为:5﹣t,∵C(﹣3,2),∴点P的坐标(﹣3,5﹣t);
③能确定,当3<t<5时,∵BC=3,∴点P在CD上,如图,过P作PF∥BC交AB于F,
则PF∥AD,∴∠BPF=∠CBP=x°,∠APF=∠DAP=y°,∴∠BPA=∠BPF+∠APF=x°+y°=z°,
∴z=x+y,故答案为x+y.
5.(广益)在直角坐标系中,点O为坐标原点,A(1,1),B(1,3),将线段AB平移到直线AB的右边得到线段CD(点C与点A对应,点D与点B对应),点D的坐标为(m,n),且m>1.
(1)如图1,当点C坐标为(2,0)时,请求出三角形BCD的面积;
(2)如图2,点E是线段CD延长线上的点,∠BDE的平分线DF交射线AB于点F.试问:的值是否会改变,若不变,请求其值;若改变,请说明理由.
(3)如图3,线段CD运动的过程中,在(2)的条件下,n=4.
①当m=4时,在直线AB上点P,满足三角形PBC的面积等于三角形CDF的面积,请求出点P的坐标;
②若点Q在x轴上,满足三角形QBC的面积等于三角形CDF的面积的2倍,请直接写出点Q的坐标.(用含m的式子表示)
【解答】(1)解:如图1中,∵C(2,0),D(2,2),B(1,3),∴S△BCD=×2×1=1.
(1) 不会发生变化.证明:如图2中,∵线段AB平移得到线段CD(点C与点A对应,点D与点B对应),∴AB∥CD,AC∥BD.∴∠AFD=∠FDE,∠C=∠BDE.∵DF是∠BDE的角平分线,∴∠BDE=2∠FDE.∴∠BDE=2∠AFD.∴∠C=2∠AFD,∴=2.
(3)解:①如图3中,设P(1,m).由题意 •|m﹣3|•3=×2×3,解得m=5或1,∴P1(1,5),P2(1,1);②如图3﹣1中,在BA的延长线上取一点G(1,﹣1),连接CG、CB、CF.
易证S△BCG=2S△DCF,过点G作GQ∥BC交x轴于Q,此时S△QBC=S△GBC=2S△DCF,∵B(1,3),C(m,2),∴直线BC的解析式为y=x+,∴直线QG的解析式为y=x+,令y=0,得到x=2﹣m,∴Q(2﹣m,0),在射线DE取K(m,6),则S△KBC=2S△DCF,过点K作BC的平行线交x轴于Q′,此时S△Q′BC=2S△DCF,由直线KQ′的解析式为:y=x+,令y=0,得到x=7m﹣6,∴Q′(7m﹣6,0).综上所述,满足条件的点P坐标为(2﹣m,0)或(7m﹣6,0).
6.(青竹湖)在平面直角坐标系中,、、,其中、、满足关系
.
(1)如图1,求的面积;
(2)如图2,在负半轴上有一点,满足,的角平分线与的角平分线相交于点,点是延长线上一点,且,求的值;
(3)如图3,若将线段向上平移个单位长度,点为轴上一点,点为第一象限内一动点,连、、,若的面积等于由、、、四条线段围成的图形的面积,求点的坐标(用含的式子表示).
【解答】解:(1)∵+|a﹣b+4|+(c﹣5)2=0.∴,解得:,
∴A(﹣2,0),B(2,4),C(5,0),∴△ABC的面积===14;
(2)如图2,∵DB⊥BC,
∴∠DBC=90°,∴∠BDC+∠BCD=90°,∵DP平分∠BDC,PC平分∠BCD,∴∠PDC=∠BDC,∠PCD=∠BCD,∴∠PDC+∠PCD=(∠BDC+∠BCD)=45°,∴∠EPD=∠PDC+∠PCD=45°,
∵∠EBD=∠EPD=45°,∠EMB=∠DMP,∴∠BEC=∠BDP,∴==;
(3)如图3,平移后的点A(﹣2,1),B(2,5),
将四边形ABFC拓展成长方形HDCM,则S四边形ABFC=S长方形HDCM﹣S△ABH﹣S△ADC﹣S△BFM,
=7×5﹣×(5+2)×1﹣,=16+n,设G(x,0),分两种情况:
①当点G在x轴的正半轴上时,如图3,延长BA交x轴于点R,同理得:S△ABG=5(x+2)﹣﹣﹣=2x+6,∵S△ABG=S四边形ABFC,∴2x+6=16+n,x=5+n,
∴G(5+n,0)
②当点G在x轴的负半轴上时,如图4,同理作长方形MGNB,过A作AQ⊥NB于Q,
∴S△ABG=5(2﹣x)﹣﹣=﹣2x﹣6,
∵S△ABG=S四边形ABFC,∴﹣2x﹣6=16+n,x=﹣11﹣n,∴G(﹣11﹣n,0)
综上,点G的坐标为:(5+n,0)或(﹣11﹣n,0).
7.(一中)在平面直角坐标系中,A(a,0),C(0,c)且满足:(a+6)2+=0,长方形ABCO在坐标系中(如图)点O为坐标系的原点.
(1)求点B的坐标.
(2)如图1,若点M从点A出发,以2个单位/秒的速度向右运动(不超过点O),点N从原点O出发,以1个单位/秒的速度向下运动(不超过点C),设M、N两点同时出发,在它们运动的过程中,四边形MBNO的面积是否发生变化?若不变,求其值;若变化,求变化的范围.
(3)如图2,E为x轴负半轴上一点,且∠CBE=∠CEB,F是x轴正半轴上一动点,∠ECF的平分线CD交BE的延长线于点D,在点F运动的过程中,请探究∠CFE与∠D的数量关系并说明理由.(注:三角形三个内角的和等于180°)
【解答】解:(1)∵(a+6)2+=0,∴a=﹣6,c=﹣3,∴A(﹣6,0),C(0,﹣3),
∵四边形OABC是长方形,∴AO∥BC,AB∥OC,AB=OC=3,AO=BC=6,∴B(﹣6,﹣3);
(2)四边形MBNO的面积不变.设M、N同时出发的时间为t,
则S四边形MBNO=S长方形OABC﹣S△ABM﹣S△BCN=18﹣×2t×3﹣×6×(3﹣t)=9.与时间无关.
∴在运动过程中面积不变.是定值9;
(3)∠CFE=2∠D.理由如下:如图
∵∠CBE=∠CEB,∴∠ECB=180°﹣2∠BEC,CD平分∠ECF,∴∠DCE=∠DCF,
∵AF∥BC,∴∠CFE=180°﹣∠DCF﹣∠DCE﹣∠BCE=180°﹣2∠DCE﹣(180°﹣2∠BEC),
∴∠CFE=2∠BEC﹣2∠DCE,∵∠BEC=∠D+∠DCE,∴∠CFE=2(∠D+∠DCE)﹣2∠DCE,
∴∠CFE=2∠D.
8.(中雅培粹)在平面直角坐标系中,,且满足:,长方形在坐标系中(如图),点为坐标系的原点.
(1)求点的坐标.
(2)如图1,若点从点出发,以2个单位/秒的速度向右运动(不超过点),点从原点出发,以1个单位/秒的速度向下运动(不超过点),设、两点同时出发,在它们运动的过程中,四边形的面积是否发生变化?若不变,求其值;若变化,求变化的范围.
(3)如图2,为轴负半轴上一点,且,是轴正半轴上一动点,的平分线交的延长线于点,在点运动的过程中,请探究与的数量关系,并说明理由。
【解答】解:(1)∵(a+6)2+=0,∴a=﹣6,c=﹣3,∴A(﹣6,0),C(0,﹣3),
∵四边形OABC是长方形,∴AO∥BC,AB∥OC,AB=OC=3,AO=BC=6,∴B(﹣6,﹣3);
(2)四边形MBNO的面积不变.设M、N同时出发的时间为t,
则S四边形MBNO=S长方形OABC﹣S△ABM﹣S△BCN=18﹣×2t×3﹣×6×(3﹣t)=9.与时间无关.
∴在运动过程中面积不变.是定值9;
(3)∠CFE=2∠D.理由如下:如图
∵∠CBE=∠CEB,∴∠ECB=180°﹣2∠BEC,∵CD平分∠ECF,∴∠DCE=∠DCF,∵AF∥BC,
∴∠CFE=180°﹣∠DCF﹣∠DCE﹣∠BCE=180°﹣2∠DCE﹣(180°﹣2∠BEC),∴∠CFE=2∠BEC﹣2∠DCE,∵∠BEC=∠D+∠DCE,∴∠CFE=2(∠D+∠DCE)﹣2∠DCE,∴∠CFE=2∠D.
9.(明德)在平面直角坐标系中,已知点,,, 且满足, 线段交轴于点,点是轴正半轴上的一点.
(1)求出点的坐标;
(2)如图2,若,,且分别平分,,求的度数(用含的代数式表示)
(3)如图3,坐标轴上是否存在一点,使得的面积和的面积相等,若存在,求出点坐标,若不存在,请说明理由.
图3
图2
图1
【解答】解:(1)∵+(a﹣b+6)2=0,∴a+b=0,a﹣b+6=0,∴a=﹣3,b=3,∴A(﹣3,0),B(3,3);
(2)如图2,过点M作MN∥DB,交y轴于点N,
∴∠DMN=∠BDM,又∵DB∥AC,∴MN∥AC,∴∠AMN=∠MAC,∵DB∥AC,∠DOC=90°,
∴∠BDO=90°,又∵AM,DM分别平分∠CAB,∠ODB,∠BAC=a,∴∠MAC=a,∠BDM=45°,
∴∠AMN=a,∠DMN=45°,∴∠AMD=∠AMN+∠DMN=45°+a;
(3)存在.连接OB,如图3,
设F(0,t),∵S△AOF+S△BOF=S△AOB,∴•3•t+•t•3=×3×3,解得t=,∴F点坐标为(0,),
△ABC的面积=×7×3=,当P点在y轴上时,设P(0,y),∵S△ABP=S△APF+S△BPF,
∴•|y﹣|•3+•|y﹣|•3=,解得y=5或y=﹣2,∴此时P点坐标为(0,5)或(0,﹣2);
当P点在x轴上时,设P(x,0),则•|x+3|•3=,解得x=﹣10或x=4,∴此时P点坐标为(﹣10,0),综上可知存在满足条件的点P,其坐标为(0,5)或(0,﹣2)或(﹣10,0).
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2022/3/16 18:06:52;用户:李昊;邮箱:2819221653@qq.com;学号:3
96810.(中雅)如图,在平面直角坐标系中,AB⊥x轴,垂足为A,BC⊥y轴,垂足为C,已知A(a,0),C(0,c),其中a,c满足关系式(a﹣6)2+|c+8|=0,点P从O点出发沿折线OA﹣AB﹣BC的方向运动到点C停止,运动的速度为每秒2个单位长度,设点P的运动时间为t秒.
(1)在运动过程中,当点P到AB的距离为2个单位长度时,t= ;
(2)在点P的运动过程中,用含t的代数式表示P点的坐标;
(3)当点P在线段AB上的运动过程中,射线AO上一点E,射线OC上一点F(不与C重合),连接PE,PF,使得∠EPF=70°,求∠AEP与∠PFC的数量关系.
【解答】解:(1)∵a,c满足关系式(a﹣6)2+(c+8)2=0,∴a﹣6=0,C+8=0,∴a=6,c=﹣8,
∴B(6,﹣8).当点P到AB的距离为2个单位长度时,s=6﹣2=4,或s=6+8+2=16,∴4÷2=2s或16÷2=8s,
(2)①当0≤t≤3时,点P在OA上,此时,P(2t,0).②当3≤t≤7时,点P在AB上,此时,PA=2t﹣6,由于点P在第四象限,纵坐标小于0,则P(6,6﹣2t).③当7≤t≤10时,点P在BC上,此时PB=2t﹣OA﹣AB=2t﹣14,PC=BC﹣PB=6﹣(2t﹣14)=20﹣2t.∴P(20﹣2t,﹣8).
(3)当点P在线段AB上时,分两种情况:
①如图3中,结论:∠PEA+∠PFC=160°,理由如下:
连接OP,∵∠PFC=∠FPO+∠FOP,∠AEP=∠EOP+∠EPO,
∴∠PEA+∠PFC=∠FPO+∠FOP+∠EOP+∠EPO=∠AOF+∠EPF=90°+70°=160°;
②如图4中,结论:∠PFC﹣∠AEP=20°,理由如下:设PM交OC于G,
∵∠AEP+∠EGO=90°,∠EGO=∠PGF=110°﹣∠PFC,∴∠AEP+110°﹣∠PFC=90°,
∴∠PFC﹣∠AEP=20°,综上所述,∠PFC+∠PEA=160°或∠PFC﹣∠AEP=20°.
第3类:坐标系中的定义新运算问题
11.(广益)在平面直角坐标系中,对于点A(x,y),若点B的坐标为(x+ay,ax+y),则称点B是点A的a级亲密点.例如:点A(﹣2,6)的级亲密点为B,即点B的坐标为(1,5).
(1)①已知点C(﹣1,5)的3级亲密点是点D,则点D的坐标为 .
②已知点P的2级亲密点是点Q(4,8),则点P的坐标为 .
(2)已知点M(m﹣1,2m)的﹣3级亲密点M1位于y轴上,求点M1的坐标.
(3)若点E在x轴上,点E不与原点重合,点E的a级亲密点为点F,且EF的长度为OE长度的倍,求a的值.
【解答】解:(1)①∵点C(﹣1,5)的3级亲密点是点D,∴D(﹣1+3×5,3×(﹣1)+5),
即D(14,2),
②设点P的坐标为(x,y),依题意得,解得,点P的坐标为(4,0),
(2)依题意得m﹣1﹣3×2m=0,解得m=﹣,∴﹣3(m﹣1)+2m=﹣m+3=+3=,∴M1(0,),
(3)设点E的坐标为(x,0),则点E的a级亲密点为点F为(x,ax),∴EF=|ax|,∵EF的长度为OE长度的倍,∴|ax|=|x|,∴a=或﹣.
12.(雅礼)在平面直角坐标系中,规定:对于任意两点P1(x1,y1)和P2(x2,y2)的“雅实距离”记为:雅P1P2=|x1﹣x2|+|y1﹣y2|.
(1)若P1(1,5),P2(3,4).求点P1,P2的“雅实距离”雅P1P2的值;
(2)已知A(﹣2,0),B为y轴上的动点;
①若点A与点B的“雅实距离”为5,求B点的坐标;
②求点A与点B的“雅实距离”的最小值;
(3)已知点C(m,2m+3),D(1,8),求点C与点D的“雅实距离”的最小值及取最小值时C点的坐标.
【解答】解:(1)∵P1(1,5),P2(3,4),∴雅P1P2=|1﹣3|+|5﹣4|=2+1=3;
(2)①设B点的坐标为(0,b),∵A(﹣2,0),B(0,b),点A与点B的“雅实距离”为5,
∴|﹣2﹣0|+|0﹣b|=5,整理得,2+|b|=5,解得,b=±3,∴B点的坐标为(0,3)或(0,﹣3);
②点A与点B的“雅实距离”为|﹣2﹣0|+|0﹣b|=2+|b|,∵|b|≥0,∴|b|+2≥2,即点A与点B的“雅实距离”的最小值为2;
(3)∵点C(m,2m+3),D(1,8),∴点C与点D的“雅实距离”为|m﹣1|+|2m+3﹣8|=|m﹣1|+|2m﹣5|,当m﹣1<0,即m<1时,原式化为:1﹣m+5﹣2m=6﹣3m>3,当m﹣1≥0,2m﹣5≤0,1≤m≤时,原式化为:m﹣1+5﹣2m=4﹣m,当m=时,4﹣m最小,最小值为,
当2m﹣5>0,即m>时,原式化为:m﹣1+2m﹣5=3m﹣6>,
综上所述,当m=时,点C与点D的“雅实距离”的最小,最小值为,此时点C的坐标为(,8).
13.(中雅)如图,对于平面直角坐标系中的任意两点A,B给出如下定义:过点A作直线m⊥x轴,过点B作直线n⊥y轴,直线m,n交于点C,我们把BC叫做A,B两点之间的水平宽,记作d1(A,B),即d1(A,B)=|xA﹣xB|,把AC叫做A,B两点之间的铅垂高,记作d2(A,B),即d2(A,B)=|yA﹣yB|.
特别地,当AB⊥x轴时,规定A,B两点之间的水平宽为0,即d1(A,B)=0,A,B两点之间的铅垂高为线段AB的长,即d2(A,B)=|yA﹣yB|;
当AB⊥y轴时,规定A,B两点之间的水平宽为线段AB的长,即d1(A,B)=|xA﹣xB|,A,B两点之间的铅垂高为0,即d2(A,B)=0;
(1)已知O为坐标原点,点P(2,﹣1),则d1(O,P)= 2 ,d2(O,P)= 1 .
(2)已知点Q(3t,﹣2t+2).
①若点D(0,2),d1(Q,D)+d2(Q,D)=5,求t的值;
②若点D(﹣2t,3t),直接写出d1(Q,D)+d2(Q,D)的最小值.
【解答】解:(1)由题意,d1(O,P)=|2﹣0|=2,d2(O,P)=|0﹣(﹣1)|=1,
(2)①由题意:|3t|+||2t|=5,当t>0时,t=1,当t<0时,t=﹣1,综上所述,t的值为±1.
②由题意,d1(Q,D)+d2(Q,D)=|5t|+|5t﹣2|,当t≤0时,d1(Q,D)+d2(Q,D)=|5t|+|5t﹣2|=2﹣10t,t=0时,有最小值,最小值为2,当0<t<时,d1(Q,D)+d2(Q,D)=|5t|+|5t﹣2|=5t+2﹣5t=2,当t≥时,d1(Q,D)+d2(Q,D)=|5t|+|5t﹣2|=10t﹣2,t=时,有最小值,最小值为2,
综上所述,d1(Q,D)+d2(Q,D)的最小值为2.
人教版七年级下册第五章 相交线与平行线综合与测试练习: 这是一份人教版七年级下册第五章 相交线与平行线综合与测试练习,文件包含专题08平行线的性质与判定的证明题重难点题型分类解析版-人教版doc、专题08平行线的性质与判定的证明题重难点题型分类原卷版-人教版doc等2份试卷配套教学资源,其中试卷共22页, 欢迎下载使用。
人教版七年级下册第六章 实数综合与测试同步达标检测题: 这是一份人教版七年级下册第六章 实数综合与测试同步达标检测题,文件包含专题10实数重难点题型分类解析版-人教版docx、专题10实数重难点题型分类原卷版-人教版docx等2份试卷配套教学资源,其中试卷共16页, 欢迎下载使用。
初中数学人教版七年级下册第七章 平面直角坐标系综合与测试练习: 这是一份初中数学人教版七年级下册第七章 平面直角坐标系综合与测试练习,文件包含专题11平面直角坐标系重难点题型分类解析版docx、专题11平面直角坐标系重难点题型分类原卷版docx等2份试卷配套教学资源,其中试卷共19页, 欢迎下载使用。














