人教版数学七年级下册 第七章《平面直角坐标系》章节复习课件+章节教学设计+章节复习导学案+单元测试卷（含答案解析）

这是一份人教版数学七年级下册 第七章《平面直角坐标系》章节复习课件+章节教学设计+章节复习导学案+单元测试卷（含答案解析），文件包含人教版数学七年级下册第七章《平面直角坐标系》章节复习课件pptx、人教版数学七年级下册第七章《平面直角坐标系》章节复习教学设计docx、人教版数学七年级下册第七章《平面直角坐标系》章节复习导学案docx等3份课件配套教学资源，其中PPT共44页， 欢迎下载使用。

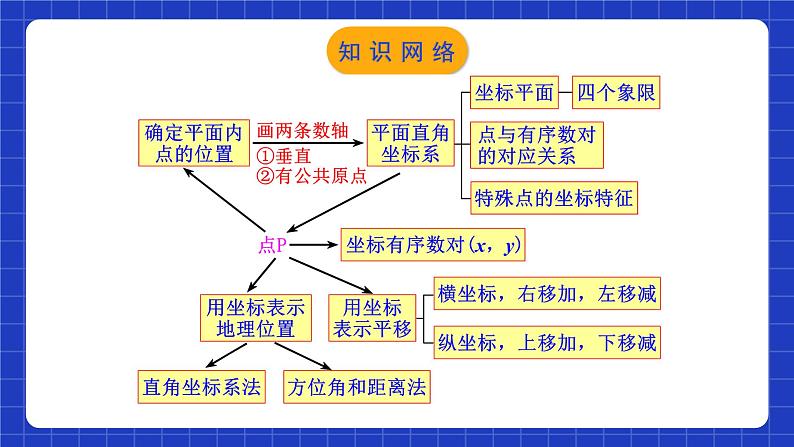
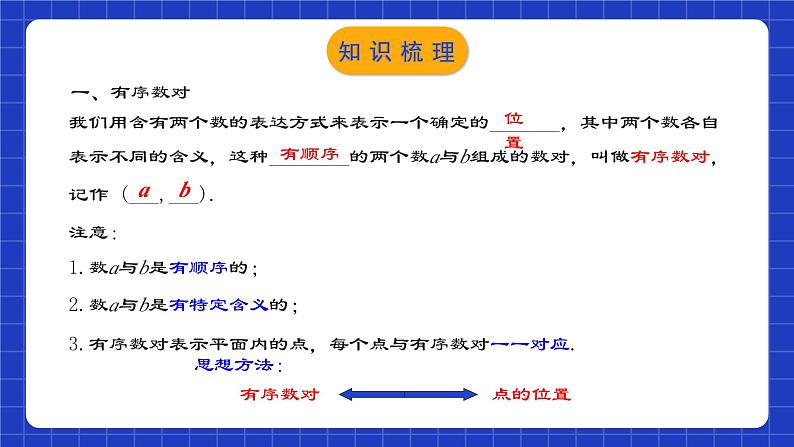
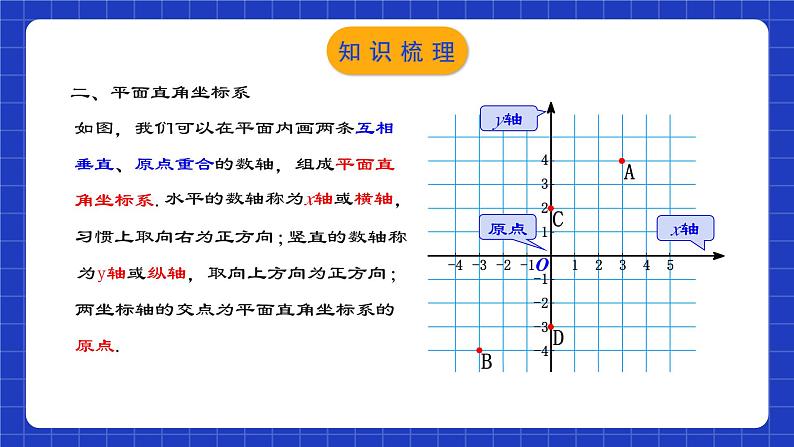
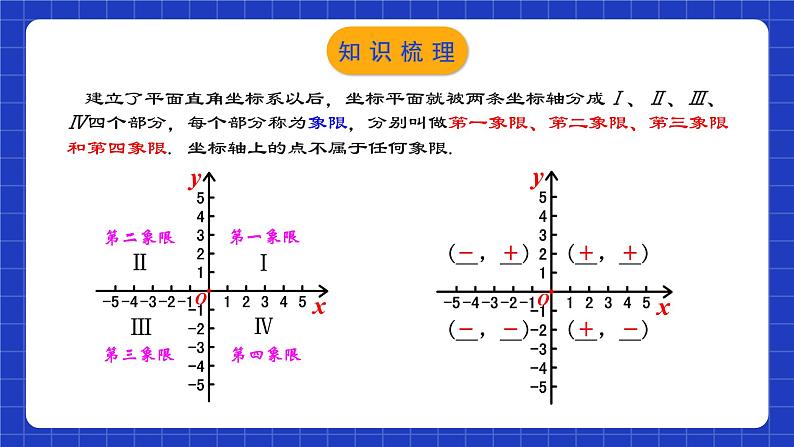
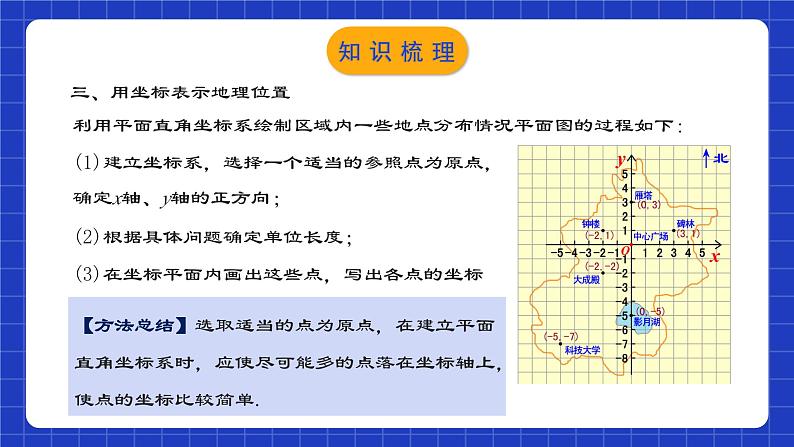
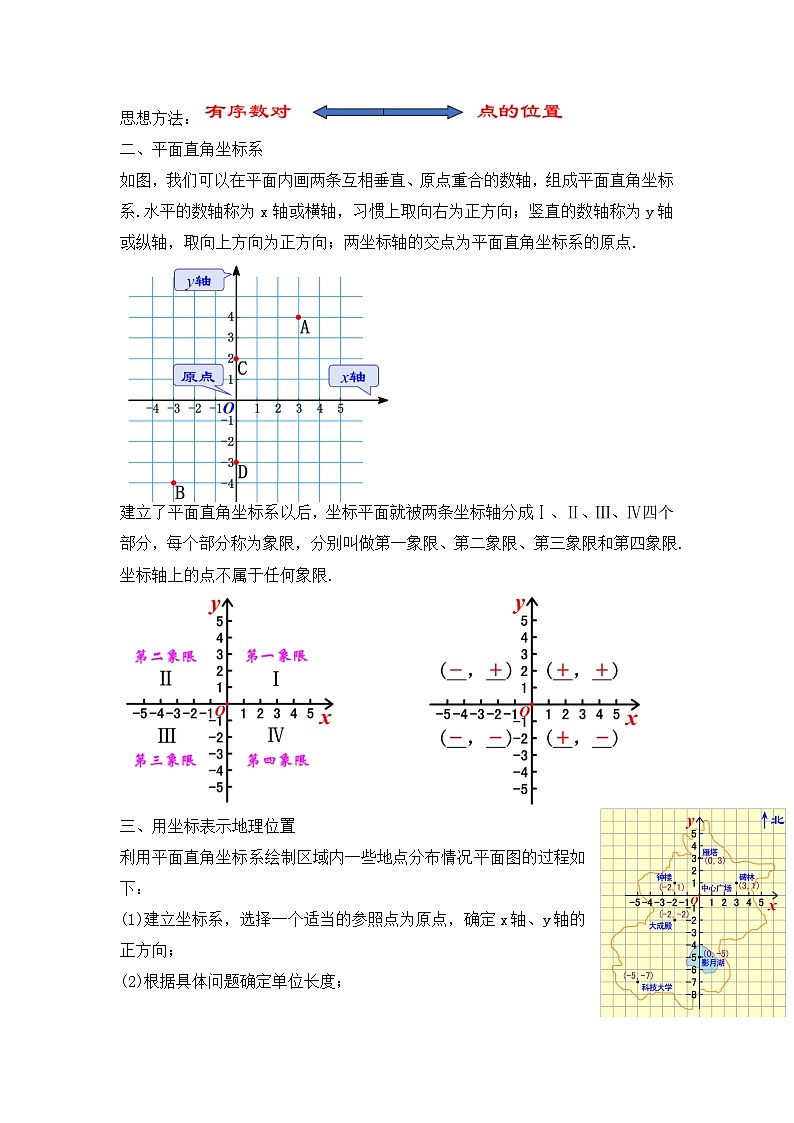
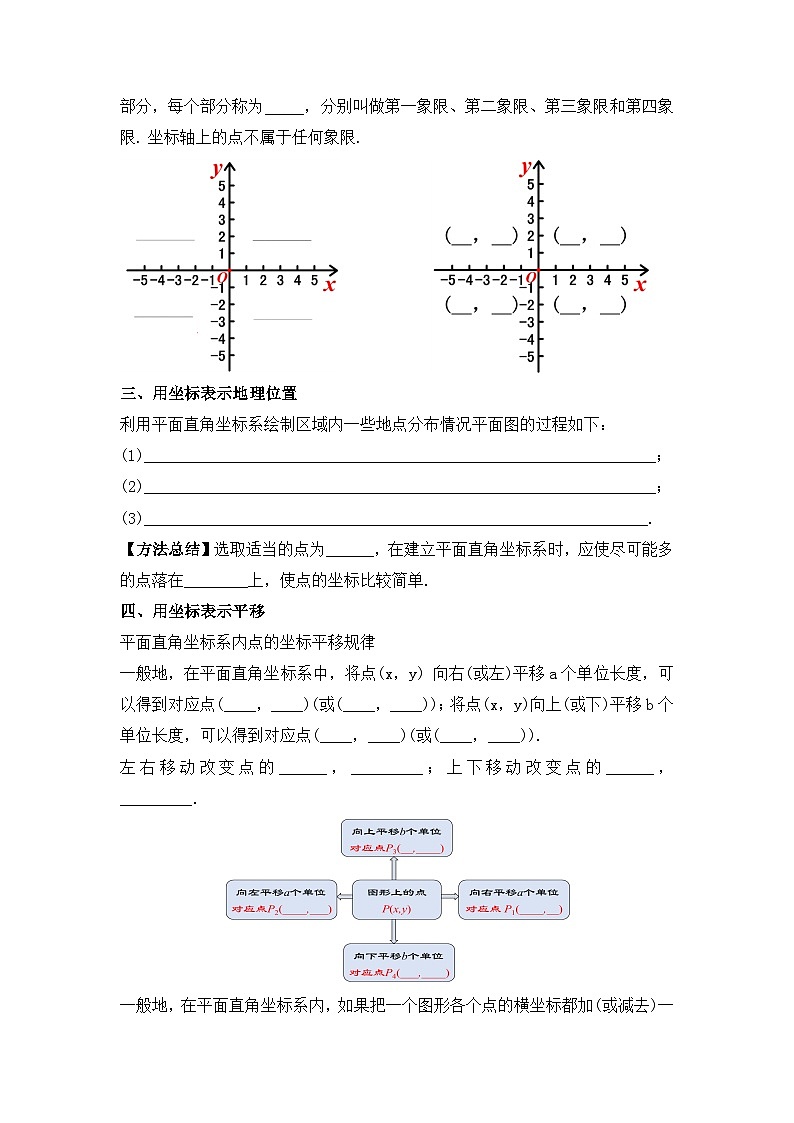
平面直角坐标系 章节复习学习目标1.熟练掌握本章的知识结构及各知识点间的相互关系;2.灵活运用相关知识解决与坐标有关的计算，熟练画出平移后的图形并用坐标表示平移; (重点)3.平面直角坐标系中的变化规律.(难点)知识网络我们用含有两个数的表达方式来表示一个确定的_______，其中两个数各自表示不同的含义，这种________的两个数a与b组成的数对，叫做有序数对，记作 (___,___).位置有顺序ab注意：1.数a与b是有顺序的；2.数a与b是有特定含义的；3.有序数对表示平面内的点，每个点与有序数对一一对应.一、有序数对知识梳理如图，我们可以在平面内画两条互相垂直、原点重合的数轴，组成平面直角坐标系. 水平的数轴称为x轴或横轴，习惯上取向右为正方向； 竖直的数轴称为y轴或纵轴，取向上方向为正方向；两坐标轴的交点为平面直角坐标系的原点.x轴y轴原点二、平面直角坐标系知识梳理建立了平面直角坐标系以后，坐标平面就被两条坐标轴分成Ⅰ、Ⅱ、Ⅲ、Ⅳ四个部分，每个部分称为象限，分别叫做第一象限、第二象限、第三象限和第四象限. 坐标轴上的点不属于任何象限.知识梳理利用平面直角坐标系绘制区域内一些地点分布情况平面图的过程如下：(1)建立坐标系，选择一个适当的参照点为原点，确定x轴、y轴的正方向；(2)根据具体问题确定单位长度；(3)在坐标平面内画出这些点，写出各点的坐标和各个地点的名称.【方法总结】选取适当的点为原点，在建立平面直角坐标系时，应使尽可能多的点落在坐标轴上，使点的坐标比较简单.三、用坐标表示地理位置知识梳理一般地，在平面直角坐标系中，将点(x，y) 向右(或左)平移a个单位长度，可以得到对应点(____，____)(或(____，____))；将点(x，y)向上(或下)平移b个单位长度，可以得到对应点(____，____)(或(____，____)).xy+bx+ayx-ayxy-b左右移动改变点的横坐标，左减右加；上下移动改变点的纵坐标，下减上加．平面直角坐标系内点的坐标平移规律四、用坐标表示平移知识梳理向左平移a个单位对应点P2(x-a,y)向右平移a个单位对应点 P1(x+a,y)向上平移b个单位对应点P3(x,y+b)向下平移b个单位对应点P4(x,y-b) 图形上的点P(x,y)平面直角坐标系内点的坐标平移规律知识梳理一般地，在平面直角坐标系内，如果把一个图形各个点的横坐标都加(或减去)一个正数a，相应的新图形就是把原图形向右(或向左)平移a个单位长度；如果把它各个点的纵坐标都加(或减去)一个正数a，相应的新图形就是把原图形向上(或向下)平移a个单位长度.知识梳理考点梳理01有序数对及其应用例1.如图，一只甲虫在10×10的方格(每小格边长为1).上沿着网格线运动.它从C处出发想去看望A、B、D、E处的其他甲虫，规定其行动:向上向右走为正，向下向左走为负.如果从C到B记为C→B(-5,-2)(第一个数表示左、右方向，第二个数表示上、下方向)，那么(1)C→D (___，___) ; B→C (___，___) ; D→____(-5,+6); E→____(___，+4).-2-4+5+2AD-5考点解析例1.如图，一只甲虫在10×10的方格(每小格边长为1).上沿着网格线运动.它从C处出发想去看望A、B、D、E处的其他甲虫，规定其行动:向上向右走为正，向下向左走为负.如果从C到B记为C→B(-5,-2)(第一个数表示左、右方向，第二个数表示上、下方向)，那么(2)若这只甲虫的行走路线是C→A→B→D→E，请计算甲虫走过的路程.解:∵C→A(-7,2)→B(2,-4)→D(3,-2)→E(5,-4）∴总路程为:|-7|+|2|+|2|+|-4|+|3|+|-2|+|5|+|-4|=29.考点解析【1-1】下列数据不能确定物体位置的是( )A.A栋4楼 B.1单元6楼8号 C.和平路125号 D.东经110°，北纬74°【1-2】如图，雷达探测器测得六个目标A、B、C、D、E、F出现，按照规定的目标表示方法，目标C、F的位置分别表示为C(6，120°)、 F(5, 210°), 按照此方法在表示目标A、B、D、E的位置时，其中表示不正确的是( )A.A(5,30°) B.B(2,90°)C.D(4,240°) D.E(3,60°)AD迁移应用【1-3】象棋中有“马走日，象(相)走田”的规则，在如图所示的棋盘中，如果“相”的位置表示为(5，8)， 则“相”走一步之后在位置不可能是( )A.(7, 6)B.(7,10)C.(2，6)D.(3,10)C迁移应用例2.在平面直角坐标系中描出下列各点：A(4，5)，B(-2，3)，C(-4，-1)，D(2.5，-2)，E(0，-4). 解：如图，先在x轴上找出表示4的点，再在y轴上找出表示5的点，过这两个点分别作x轴和y轴的垂线，垂线的交点就是点A.A(4，5)E(0，-4) B(-2，3)C(-4，-1)D(2.5，-2)02平面直角坐标系与点的坐标考点解析例3.设点M(a，b)为平面直角坐标系内的点．(1)当a>0，b<0时，点M位于第几象限？(2)当ab>0时，点M位于第几象限？(3)当a为任意有理数，且b<0时，点M位于第几象限？解：(1)点M在第四象限；(2)在第一象限(a>0，b>0)或者在第三象限(a<0，b<0)；(3)在第三象限(a<0，b<0)或者第四象限(a>0，b<0)或者y轴负半轴上(a=0，b<0)．考点解析  考点解析【2-1】下列各点中，在第二象限的点是( )A.(2，3) B.(2，-3) C.(-2，3) D.(-2，-3)【2-2】点P在第三象限内，P到x轴的距离是4，到y轴的距离是3,那么点P的坐标是( )A.(-4，3) B.(-3，-4) C.(-3，4) D.(3，-4)CB迁移应用【2-3】若点P(x, y)在第四象限，且|x|=5， |y|=6，则点P的坐标是( )A.(-5，-6) B.(-5，6) C.(5，-6) D.(5，6)C【2-4】如图，点A的坐标是________,点B的坐标是_________,点C的坐标是_________,点D的坐标是__________,点E的坐标是__________,点F的坐标是________,点G的坐标是________,点H的坐标是________.(-2，4)(-4，2)(-4，-2)(-2，-4)(2，-4)(4，-2)(4，2)(2，4)迁移应用  迁移应用  迁移应用03平面直角坐标系中点的坐标特征应用例5.点P(a，b)在第二象限内，则Q(-b2，-a+b)在第_____象限．解：∵点P(a，b)在第二象限内，∴a＜0；b＞0，∴-b2＜0，-a＞0，-a+b＞0，∴Q(-b2，-a+b)在第二象限．二考点解析例6.已知点P(x2-3，1)在一、三象限夹角平分线上，则x=_____; 点Q(a+3，7+a)位于二、四象限的角平分线上，则a=_____．解：由已知条件知，点P位于一、三象限夹角平分线上，所以有x2-3=1，得x=±2．根据题意得a+3+7+a=0，解得a=-5．-5±2考点解析【3-1】已知点P(x，y)位于第二象限，并且 y ≤2x＋6，x，y为整数，则点P的个数是_______.【3-2】已知:A(1,2),B(x,y),AB∥x轴,且B到y轴距离为2,则点B的坐标是_____________.【3-3】已知点P(x＋1，3)在第一、三象限坐标轴夹角的平分线上，则x＝_____ ；若点Q(－2，1＋y)在第二、四象限坐标轴夹角的平分线上，则y＝____.6个(2,2)或(-2,2)21迁移应用04用坐标表示地理位置的应用例7.如图所示的是某学校的平面示意图，已知旗杆的位置是（−1，2），实验室的位置是（2，3）．(1)根据所给条件建立适当的平面直角坐标系，并用坐标表示宿舍楼的位置．(2)已知办公楼的位置是（−2，1），教学楼的位置是（3，1），请在图中标出办公楼和教学楼的位置．考点解析（1）解：如图所示：宿舍楼的位置（－5，1）；（2）解：如图所示：办公楼和教学楼的位置即为所求．考点解析 （1）解：由题意得： 90°-45°=45°，90°-40°=50°， 学校在小明家北偏东45°方向2km处， 博物馆在小明家南偏东50°方向4km处；考点解析 (2)图中到小明家距离相同的是哪些地方？考点解析【4-1】以下是甲、乙、丙三人看地图时对四个地址的描述:甲:从学校向北直走500米，再向东直走100米可到图书馆;乙:从学校向西直走300米，再向北直走200米可到邮局;丙:邮局在新华书店的正西方200米处.根据三人的描述，若从图书馆出发，判断下列哪一种走法，其终点是新华书店( )A.向南直走300米，再向西直走200米B.向南直走300米，再向西直走600米C.向南直走700米，再向西直走200米D.向南直走700米，再向西直走600米A迁移应用【4-2】如图是广西几个城市旅游景点的平面示意图．(1)请选取某一个景点为坐标原点，建立平面直角坐标系；(2)在所建立的平面直角坐标系中，写出其余各景点的坐标． 迁移应用  迁移应用05用坐标表示平移的应用  4考点解析例10.如图,在平面直角坐标系中,P(a,b)是三角形ABC的边AC上一点,三角形ABC经平移后点P的对应点为P1(a＋6,b＋2)．(1)请画出上述平移后的三角形A1B1C1，并写出点A、C、A1、C1的坐标；1yO1xABC解:(1)三角形A1B1C1如图所示，各点的坐标分别为A(－3，2)、C(－2，0)、A1(3，4)、C1(4，2)；PP1考点解析(2)求出以A、C、A1、C1为顶点的四边形的面积.(2)连接AA1,CC1, 考点解析 A（3，-1）迁移应用【5-3】如图，A，B两点的坐标分别为(2，3)，(4，1).(1)求三角形ABO的面积;(2)把三角形ABO向下平移3个单位后得到一个新的三角形O'A'B'，求三角形O'A'B'的3个顶点的坐标. 迁移应用06与坐标有关的规律问题例11.如图，A1(1, 0), A2(1，1)，A3(-1, 1)，A4(-1, -1),A5(2，-1),...，则A2018的坐标为__________.【分析】依题得，A4(-1, -1)，A8(-2，-2)，A12(-3，-3)，…，A2016(-504，-504) ，因此，A2017(505，-504)，所以，A2018(505,505).(505,505)考点解析 考点解析 考点解析 C迁移应用 (7,1)(1011,1)迁移应用 (5，0) (45，3)迁移应用课程结束