

浙江省绍兴市上虞区2021-2022学年八年级下学期期末数学试题(word版含答案)
展开2021学年第二学期八年级期末教学质量调测
数学试题卷
一、选择题(本大题有10小题,每小题3分,共30分.请选出每小题中一个符合题意的正确选项,不选、多选、错选,均不给分.)
1.当x=1时,二次根式的值等于( )
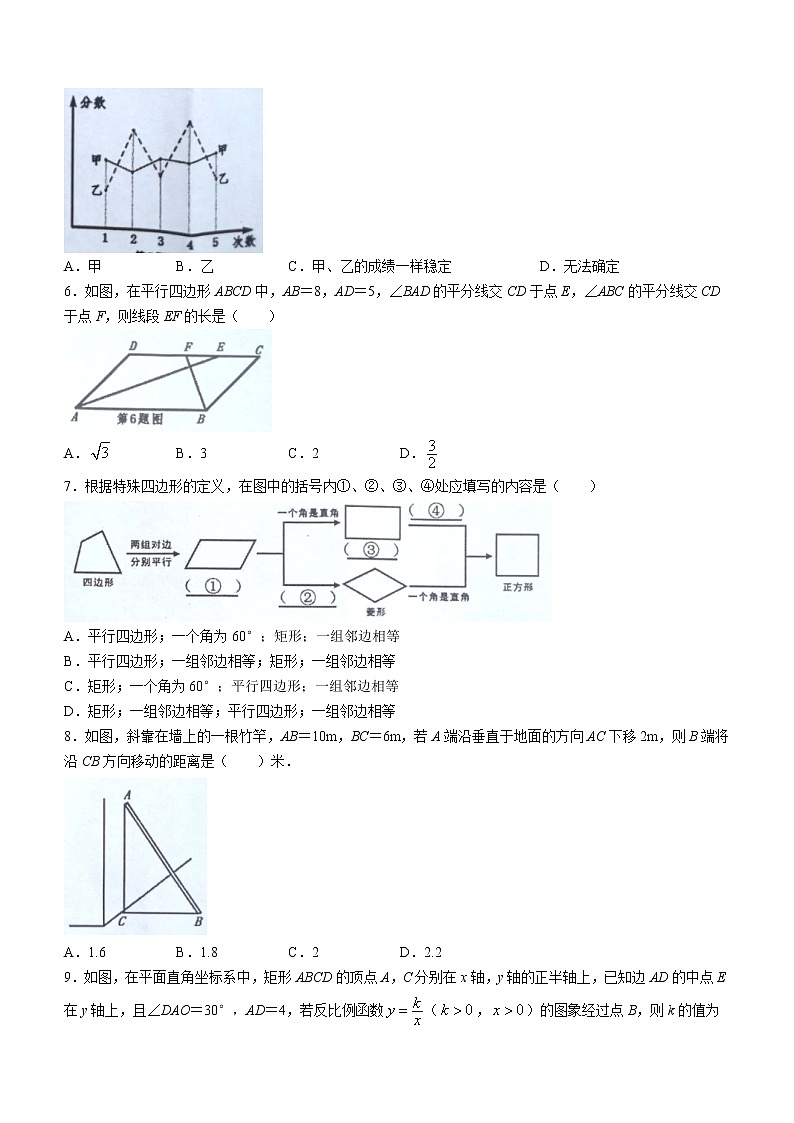
A.4 B.0 C. D.2
2.小敏所在社会实践活动小组的同学积极响应“垃圾分类,从我做起”的号召,主动到附近的7个社区宣传垃圾分类.她们记录的各社区参加活动的人数如图所示,则这组数据的众数和中位数分别是( )
A.42,40 B.42,38 C.2,40 D.2.38
3.如图,菱形花坛DEBF的面积为12平方米,其中沿对角线FE修建的小路长为4米,则沿对角线BD修建的小路长为( )米.
A.10 B.8 C.6 D.3
4.已知一元二次方程有一个根为1,则k的值为( )
A.-2 B.-4 C.2 D.4
5.如图是甲、乙两位运动员正式比赛前5次训练成绩的折线统计图,依据图中信息,你认为成绩较稳定的是( )
A.甲 B.乙 C.甲、乙的成绩一样稳定 D.无法确定
6.如图,在平行四边形ABCD中,AB=8,AD=5,∠BAD的平分线交CD于点E,∠ABC的平分线交CD于点F,则线段EF的长是( )
A. B.3 C.2 D.
7.根据特殊四边形的定义,在图中的括号内①、②、③、④处应填写的内容是( )
A.平行四边形;一个角为60°;矩形;一组邻边相等
B.平行四边形;一组邻边相等;矩形;一组邻边相等
C.矩形;一个角为60°;平行四边形;一组邻边相等
D.矩形;一组邻边相等;平行四边形;一组邻边相等
8.如图,斜靠在墙上的一根竹竿,AB=10m,BC=6m,若A端沿垂直于地面的方向AC下移2m,则B端将沿CB方向移动的距离是( )米.
A.1.6 B.1.8 C.2 D.2.2
9.如图,在平面直角坐标系中,矩形ABCD的顶点A,C分别在x轴,y轴的正半轴上,已知边AD的中点E在y轴上,且∠DAO=30°,AD=4,若反比例函数(,)的图象经过点B,则k的值为( )
A. B.8 C.6 D.
10.在Rt△ABC中,AC=3,BC=4,∠ACB=90°,点P,Q分别是边AB和BC上的动点,始终保持AP=BQ,连结AQ,CP,则的最小值为( )
A. B. C. D.6
二、填空题(本题有8小题,每小题3分,共24分.请将本题答案用签字笔或钢笔写在答题卡对应答题区域内.)
11.二次根式中,字母a的取值范围是______.
12.若x=1是一元二次方程的一个根,则m=______.
13.在学校组织的“共享好书伴你成长”活动中,八年级(1)班第一小组5名同学所分享的好书册数分别是:7,3,x,6,4.已知这组数据的中位数是5,则这组数据的方差是______.
14.已知一个多边形的内角和为1440°,则这个多边形的边数是______.
15.如图,点E为正方形ABCD外一点,且ED=CD,连结AE交BD于点F.若∠CDE=30°,则∠DFC的度数为______.
16.在纸板上剪出一个平行四边形ABCD,作出其对角线的交点O.我们进行如下操作:用大头针把一根平放在平行四边形纸板上的直细木条固定在点O处,并使细木条可以绕点O转动,拨动细木条,它可以停留在任意位置,如果设细木条与一组对边AB,CD的交点分别为点E,F,则下列结论:
①OE=OF;②AE=CF;③BE=CF;④.一定成立的是______(填写序号即可).
17.在平面直角坐标系中,经过反比例函数图象上的点A(1,5)的直线与x轴,y轴分别交于点C,D,且与该反比例函数图象交于另一点B.则______.
18.如图,正方形ABCD的边长是16,点E在边AB上,AE=3,点F是边BC上不与点B,C重合的一个动点,把△EBF沿EF折叠,点B落在处,若恰为等腰三角形,则的长为______.
三、解答题(本大题有6小题,共46分,解答需写出必要的文字说明、演算步骤或证明过程.)
19.(本题8分,每小题4分)解答下列各题:
(1)计算:.
(2)设实数的整数部分为a,小数部分为b,求的值.
20.(本题共8分,每小题4分)解答下列各题:
(1)用配方法解方程:.
(2)设,是一元二次方程的两根,求的值.
21.(本题6分)某校于近期组织开展了一次“航空航天知识”大赛,现从七、八两年级分别随机抽取了8名学生的大赛成绩,具体见下表.(本次知识大赛满分为100分,该校七、八年级学生共有1600人.)
七年级 | 96 | 85 | 90 | 86 | 81 | 92 | 95 | 81 |
八年级 | 80 | 95 | 83 | 93 | 94 | 75 | 85 | 95 |
经整理分析,获得如下不完整的数据分析统计表:
班级 | 平均数 | 中位数 | 众数 |
七年级 | 88.25 | b | 81 |
八年级 | a | 89 | c |
根据以上信息,解答下列问题.
(1)表中的a=______;b=______;c=______.
(2)若85分以上(包括85分)为优秀等级,请估计该校七、八年级共有多少名学生的成绩达到优秀等级.
(3)根据数据分析统计表中所提供的统计量,请你判断哪个年级的大赛成绩较好?并说明理由.
22.(本题8分)已知关于x的方程.
(1)求证:无论m取什么实数,这个方程总有两个不相等的实数根.
(2)若这个方程的两个实根,,满足,求m的值.
23.(本题8分)如图,一张矩形纸片ABCD,点E在边AB上,将△BCE沿直线CE对折,点B落在对角线AC上,记为点F.
(1)若AB=4,BC=3,求AE的长.
(2)连结DF,若点D,F,E在同一条直线上,且DF=2,求AE的长.
24.(本题8分)如图1,四边形ABCD是正方形,E是BC垂直平分线上的点,点E关于直线BD的对称点是,直线BE与直线交于点F.
(1)若点E是边BC的中点,连结AF.则∠FAB=______.
(2)小聪认为:只要点E不在正方形的中心,则直线AF与AB所夹锐角度数不变,小敏尝试改变点E的位置,如图2,她将点E选在正方形内,且△EAD为等边三角形,请你帮助小敏求出直线AF与AB所夹锐角∠FAB的度数,以验证小聪观点的正确性.
(3)为继续验证小聪的观点,小敏尝试进一步通过改变点E的位置,探究计算出相应角度.以下是小敏提出的两种验证途径:
A.将点E选在边AD的中点处.
B.将点E选在正方形外,且使∠EBC=45°的位置.
请你选择其中一种途径,画出相应图形,并求直线AF与AB所夹锐角的度数.我选择途径______(填“A”或“B”)来进行验证.
思维拓展题:(本题有4小题,共10分,成绩计入总分,但全卷满分不超过100分)
1.已知AD是△ABC的中线,BC=6,且∠ADC=45°,∠B=30°,则AC=( ).
A. B. C. D.6
2.用[x]表示不大于x的最大整数,则方程的解的个数是( ).
A.1 B.2 C.3 D.4
3.如图,矩形纸片ABCD中,AB=5,AD=4.将纸片折叠,使点B落在边CD上的处,折痕为AE.在折痕AE上存在一点P,该点到边CD的距离与到点B的距离相等,则该相等距离为______.
4.若关于x的方程所有根都是比1小的正实数,则实数m的取值范围是______.
上虞区2021学年第二学期八年级教学质量调测
数学卷参考答案及评分意见
一、选择题(每小题3分,共30分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | C | A | C | B | A | C | B | C | D | B |
二、填空题(每小题3分,共24分)
11. 12.1 13.2 14.10 15.105° 16.①②④
17. 18.16或
评分说明:第16题答对1个得1分;第18题答对1个得2分.
三、解答题(本题有6小题,共46分)
19.(本题8分,每小题4分)
解:(1)原式
(2)∵,
∴的整数部分为a=2,小数部分为,
∴.
20.(本题8分,每小题4分)
(1),.(各2分,共4分)
(2)解:由一元二次方程的根与系数的关系,得
,,
∴.
评分说明:第(1)小题不用配方法求解,若结果正确得2分.
21.(本题6分)
解:(1)87.5,88,95.(各1分,共3分)
(2)(名)
答:该校七、八年级共有1100名学生的成绩为优秀.
(3)由于八年级学生成绩的中位数比七年级学生成绩的中位数高,八年级学生成绩的众数高于七年级学生成绩的众数,所以八年级的成绩较好.
22.(本题8分)
证明:(1)∵,
无论m取何实数,的值都大于零.
∴这个方程总有两个不相等的实数根.
(2)∵,是方程的两个实数根,分别代入得:
①;②,
①-②得:,整理得:
.
由(1)知,∴,∴.
又∵,∴.
∴,代入原方程得:
化简得:.解得:,.
23.(本题8分)
解:(1)如图1,矩形纸片ABCD中,∵AB=4,BC=3,
故由勾股定理可得AC=5.
由折叠知:FC=BC=3,∠EFC=∠B=90°,BE=FE.
∴.
设AE=x,则.
在Rt△AFE中,,解得:.∴.
(2)如图2,矩形纸片ABCD中,
∵,∴∠DCE=∠BEC,
由折叠知:∠BEC=∠FEC,∴∠DCE=∠FEC,∴DC=DE.
又∵点D,F,E在同一条直线上,∠EFC=∠B,
∴∠DFC=90°,∴∠DFC=∠DAE=90°,
而CF=CB=DA,∴,∴AE=DF=2.
24.(本题8分)
解:(1)45°.
(2)①如图1,∵△EAD是等边三角形,∴∠EDA=∠EAD=60°,DE=EA=AD.
∵四边形ABCD是正方形,∴AD=AB,∠ADB=45°,∠DAB=90°.
∴AE=AB,.∴∠AEB=75°.
∵点是点E关于DB的对称点,
∴.∴∠FDE=30°.
∴.∴∠ADF=∠EDF.
∵DF=DF,∴.
∴FA=FE.∴∠FAE=∠FEA=75°.
∴.
(3)选择途径A:
将点E选在AD边的中点,如图2.
∵四边形ABCD是正方形,
∴,AB=AD,∠ADC=∠DAB=90°,∠ADB=∠CDB=45°.
∵点是点E关于DB的对称点,∴.
∴.∴在DC上.∴F在直线CD上.∴.
∴∠FDE=∠BAE,∠DFE=∠ABE.
∵E是AD的中点,∴AE=DE,∴.
∴AB=DF.∴AD=DF.
∵,
∴△ADF是等腰直角三角形,∴∠FAD=45°.∴∠FAB=135°.
∴直线AF与AB所夹锐角为45°.
选择途径B:
将点E选在正方形外,且使∠EBC=45°的位置.如图3,连结CE.
∵四边形ABCD是正方形,∴BA=BC,∠DBA=∠DBC=45°.
∵E在BC的垂直平分线上,∴EB=EC.∴∠EBC=∠ECB.
∵∠EBC=45°,∴∠ECB=45°,.∴EB⊥DB.
∵点是点E关于BD的对称点,∴.
∴,B,E三点共线.∴点与点F重合.
∴FB=BE,.
∴∠ABF=∠CBE..
∴∠FAB=∠ECB=45°.
思维拓展题:
1.B 2.C 3. 4.或
2021-2022学年浙江省绍兴市上虞区八年级(上)期末数学试卷: 这是一份2021-2022学年浙江省绍兴市上虞区八年级(上)期末数学试卷,共17页。试卷主要包含了填空题,解答题等内容,欢迎下载使用。
浙江省绍兴市上虞区2022-2023学年八年级下学期期末数学试题(含答案): 这是一份浙江省绍兴市上虞区2022-2023学年八年级下学期期末数学试题(含答案),共12页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022年浙江省绍兴市上虞区中考一模数学试题(含答案): 这是一份2022年浙江省绍兴市上虞区中考一模数学试题(含答案),共8页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。












