高中数学人教A版 (2019)必修 第二册6.2 平面向量的运算教学设计
展开教 案
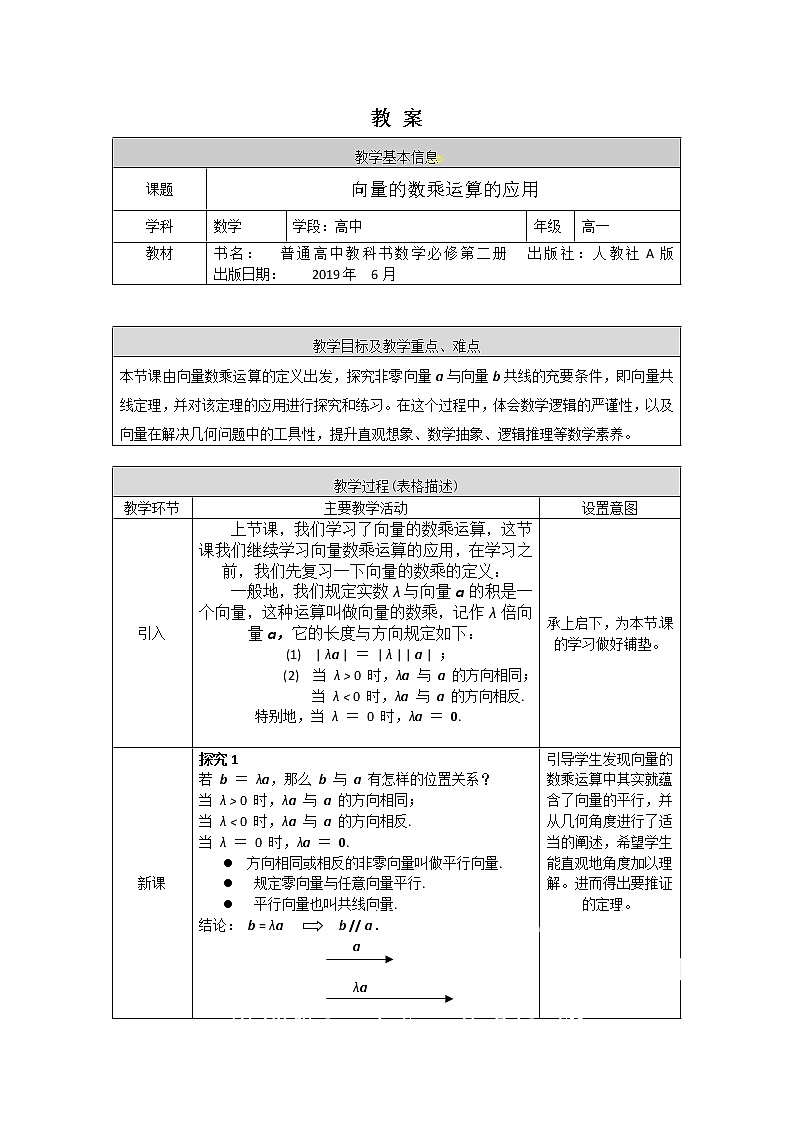
教学基本信息 | ||||
课题 | 向量的数乘运算的应用 | |||
学科 | 数学 | 学段:高中 | 年级 | 高一 |
教材 | 书名: 普通高中教科书数学必修第二册 出版社:人教社A版 出版日期: 2019年 6月 | |||
教学目标及教学重点、难点 |
本节课由向量数乘运算的定义出发,探究非零向量a与向量b共线的充要条件,即向量共线定理,并对该定理的应用进行探究和练习。在这个过程中,体会数学逻辑的严谨性,以及向量在解决几何问题中的工具性,提升直观想象、数学抽象、逻辑推理等数学素养。 |
教学过程(表格描述) | ||
教学环节 | 主要教学活动 | 设置意图 |
引入 | 上节课,我们学习了向量的数乘运算,这节课我们继续学习向量数乘运算的应用,在学习之前,我们先复习一下向量的数乘的定义: 一般地,我们规定实数λ与向量a的积是一个向量,这种运算叫做向量的数乘,记作λ倍向量a,它的长度与方向规定如下: (1) | λa | = | λ | | a | ; (2) 当 λ > 0 时,λa 与 a 的方向相同; 当 λ < 0 时,λa 与 a 的方向相反. 特别地,当 λ = 0 时,λa = 0.
| 承上启下,为本节.课的学习做好铺垫。 |
新课 | 探究1 若 b = λa,那么 b 与 a 有怎样的位置关系? 当 λ > 0 时,λa 与 a 的方向相同; 当 λ < 0 时,λa 与 a 的方向相反. 当 λ = 0 时,λa = 0. 方向相同或相反的非零向量叫做平行向量. 规定零向量与任意向量平行. 平行向量也叫共线向量. 结论: b = λa b // a . a
λa
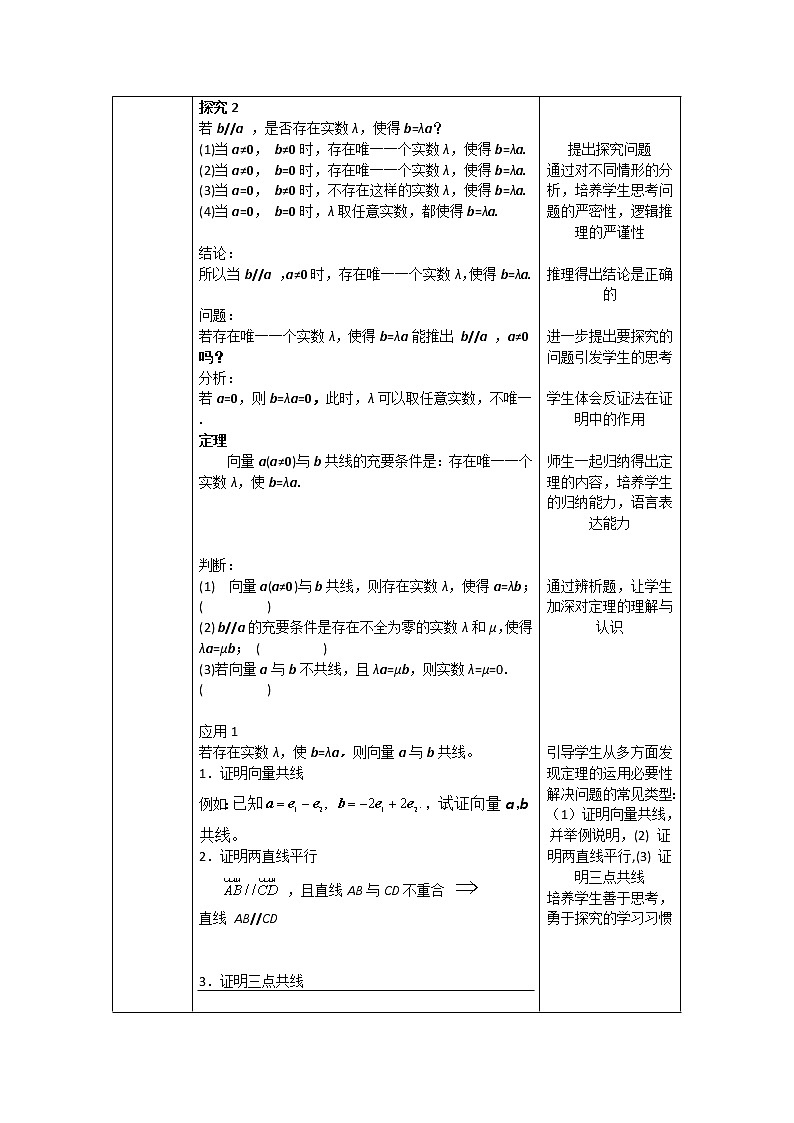
探究2 若b//a ,是否存在实数λ,使得b=λa? (1)当a≠0, b≠0时,存在唯一一个实数λ,使得b=λa. (2)当a≠0, b=0时,存在唯一一个实数λ,使得b=λa. (3)当a=0, b≠0时,不存在这样的实数λ,使得b=λa. (4)当a=0, b=0时,λ取任意实数,都使得b=λa.
结论: 所以当b//a ,a≠0时,存在唯一一个实数λ,使得b=λa.
问题: 若存在唯一一个实数λ,使得b=λa能推出 b//a ,a≠0吗? 分析: 若a=0,则b=λa=0,此时,λ可以取任意实数,不唯一 . 定理 向量a(a≠0)与b共线的充要条件是:存在唯一一个实数λ,使b=λa.
判断: (1) 向量a(a≠0)与b共线,则存在实数λ,使得a=λb; ( ) (2) b//a的充要条件是存在不全为零的实数λ和μ,使得λa=μb; ( ) (3)若向量a与b不共线,且λa=μb,则实数λ=μ=0. ( )
应用1 若存在实数λ,使b=λa,则向量a与b共线。 1.证明向量共线 例如:已知,试证向量a,b共线。 2.证明两直线平行 ,且直线AB与CD不重合 直线 AB//CD
3.证明三点共线 A,B,C三点共线 或 或 ……
| 引导学生发现向量的数乘运算中其实就蕴含了向量的平行,并从几何角度进行了适当的阐述,希望学生能直观地角度加以理解。进而得出要推证的定理。
提出探究问题 通过对不同情形的分析,培养学生思考问题的严密性,逻辑推理的严谨性
推理得出结论是正确的
进一步提出要探究的问题引发学生的思考
学生体会反证法在证明中的作用
师生一起归纳得出定理的内容,培养学生的归纳能力,语言表达能力
通过辨析题,让学生加深对定理的理解与认识
引导学生从多方面发现定理的运用必要性解决问题的常见类型: (1)证明向量共线,并举例说明,(2) 证明两直线平行,(3) 证明三点共线 培养学生善于思考,勇于探究的学习习惯
|
例题 | 例1 已知任意两个非零向量a,b,试作 ,.猜想 A,B,C三点之 间的位置关系,并证明你的猜想. 猜想:A,B,C三点共线. 证明: ∴ A,B,C三点共线.
| 通过学生操作、观察,掌握利用向量共线判断三点共线的方法,培养学生综合运用向量知识解决问题的能力,发展直观相象和逻辑推理素养。 |
新课 | 应用2 若向量a(a≠0)与b共线,则 存在唯一一个实数λ,使b=λa. 与非零向量a同向的单位向量为_______ . 与非零向量a共线的单位向量为_____.
| 进一步提出定理的用法,加深对定理的理解 |
例题 | 例2 已知a,b是两个不共线的向量,向量b-ta, 共线,求实数t的值. 解:∵ a,b不共线, , ∵ a,b不共线, ∴a // b . 与已知矛盾.
| 让学生熟练运用向量共线定理,体会知识之间的联系。 |
总结 | 本节课从复习向量数乘运算的定义出发,探究了非零向量a与向量b共线的充要条件(定理),并对该定理的应用进行了探究和练习。在这个过程中,充分体现了数学逻辑的严谨性,向量在解决几何问题中的工具性,让我们的直观想象、数学抽象、逻辑推理等数学素养得以提升。
| 总结概况所学内容,方法,让学生形成反思的习惯,提升分析问题解决问题的能力。 |
业 | 1.已知a,b是不共线的向量,且 , , ,则( ). (A) A,B,D三点共线 (B) A,B,C三点共线 (C) B,C,D三点共线 (D) A,C,D三点共线 2.已知若 , 是不共线的向量,且, ,若a与b是共线向量,求实数k的值.
| 巩固所学内容 |
高中人教A版 (2019)第六章 平面向量及其应用6.2 平面向量的运算优质教案及反思: 这是一份高中人教A版 (2019)第六章 平面向量及其应用6.2 平面向量的运算优质教案及反思,共7页。
高中数学人教A版 (2019)必修 第二册6.2 平面向量的运算教学设计: 这是一份高中数学人教A版 (2019)必修 第二册6.2 平面向量的运算教学设计,共6页。教案主要包含了预习课本,引入新课,新知探究,典例分析,课堂小结,板书设计,作业等内容,欢迎下载使用。
2020-2021学年6.3 平面向量基本定理及坐标表示教学设计: 这是一份2020-2021学年6.3 平面向量基本定理及坐标表示教学设计,共13页。













