资料中包含下列文件,点击文件名可预览资料内容


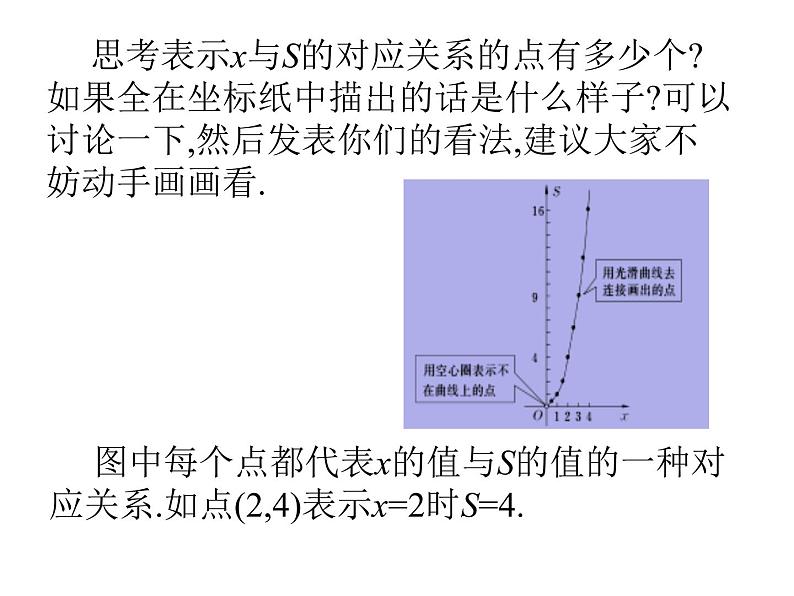


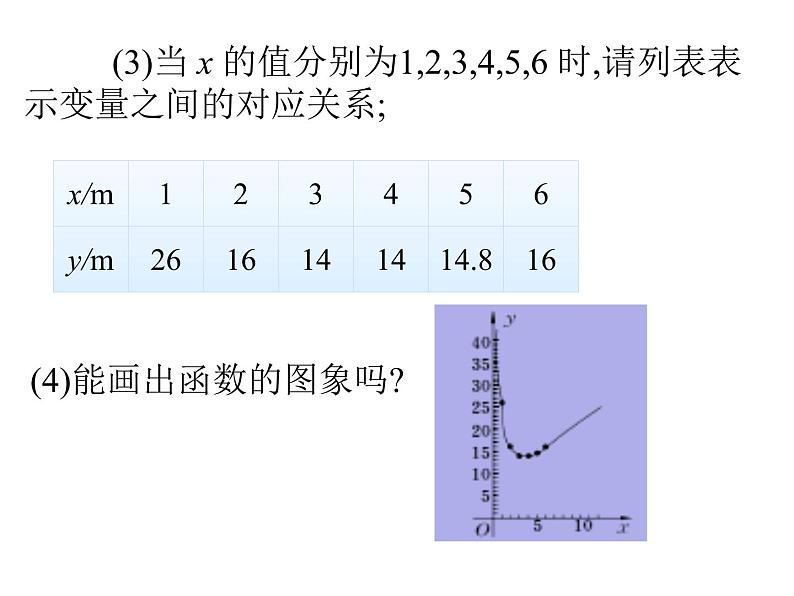








































































还剩14页未读,
继续阅读
2022春人教版八年级数学下册(课件 教学案)第十九章一次函数 (12份打包)
展开
这是一份2022春人教版八年级数学下册(课件 教学案)第十九章一次函数 (12份打包),文件包含第十九章一次函数doc、1921正比例函数第2课时pptx、1912函数的图象第1课时pptx、193课题学习选择方案pptx、1923一次函数与方程不等式pptx、1911变量与函数第2课时pptx、1911变量与函数第1课时pptx、1922一次函数第1课时pptx、1922一次函数第2课时pptx、1922一次函数第3课时pptx、1912函数的图象第2课时pptx、1921正比例函数第1课时pptx等12份课件配套教学资源,其中PPT共204页, 欢迎下载使用。
八年级数学·下 新课标[人]
第十九章 一次函数
19.2.2 一次函数(第2课时)
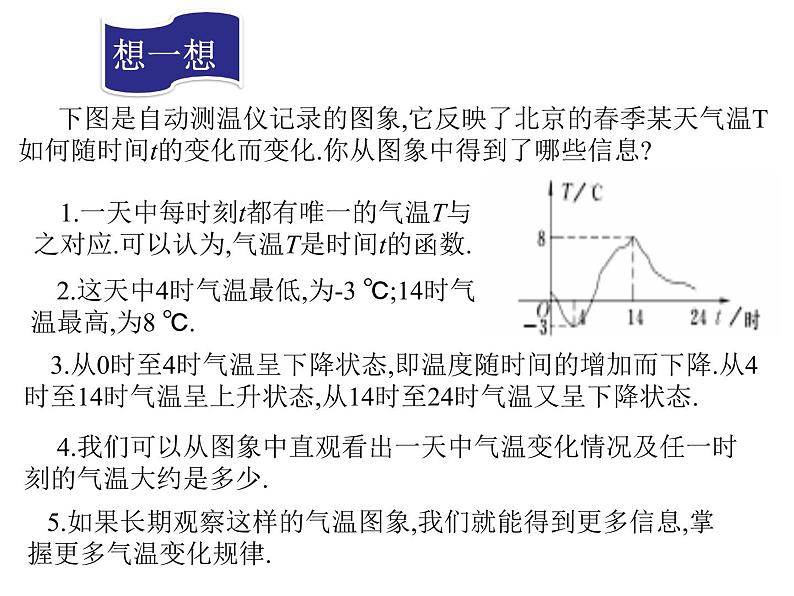
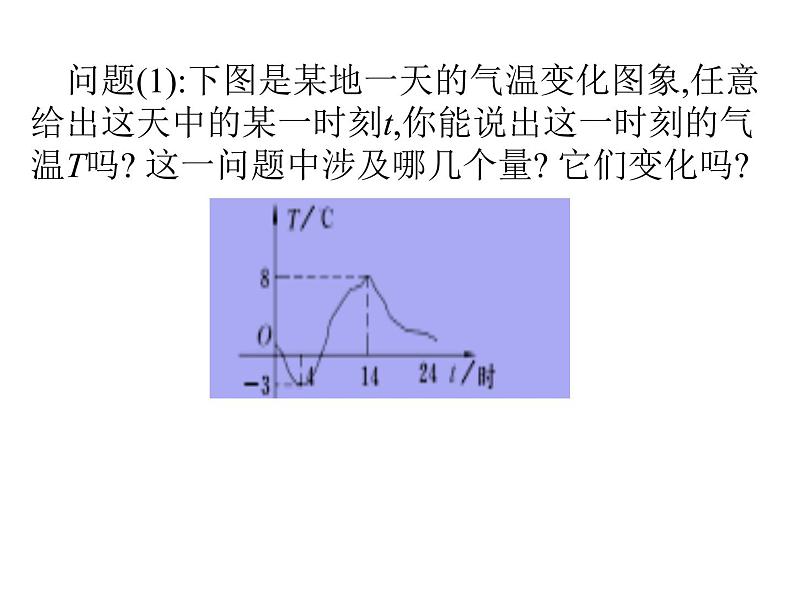
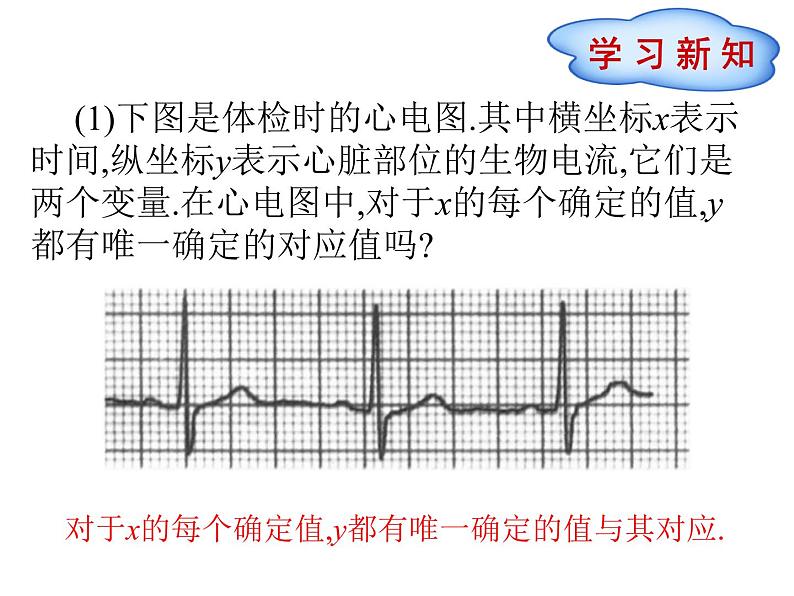
想一想
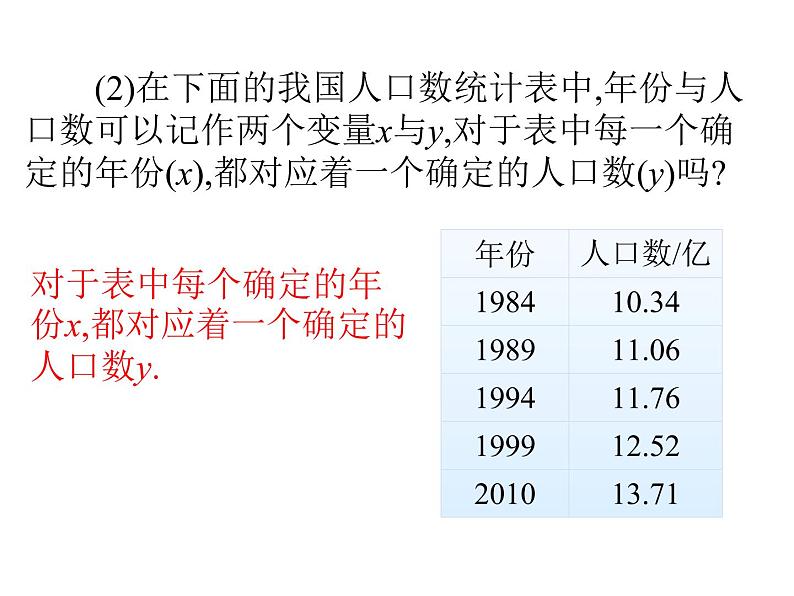
正比例函数与一次函数有何关系?
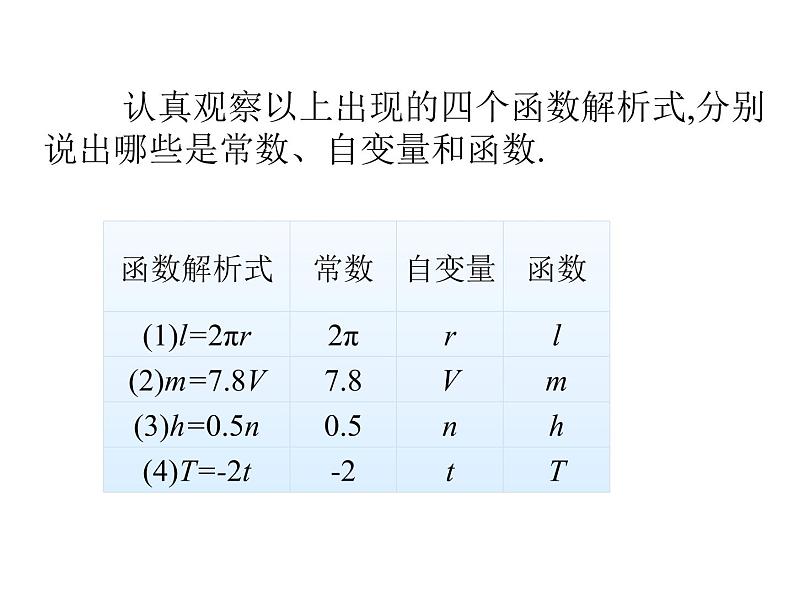
一次函数y=kx+b(k≠0),当b=0时,一次函数则为正比例函数y=kx,因此,正比例函数是当常数项b=0时的一次函数,是特殊的一次函数.
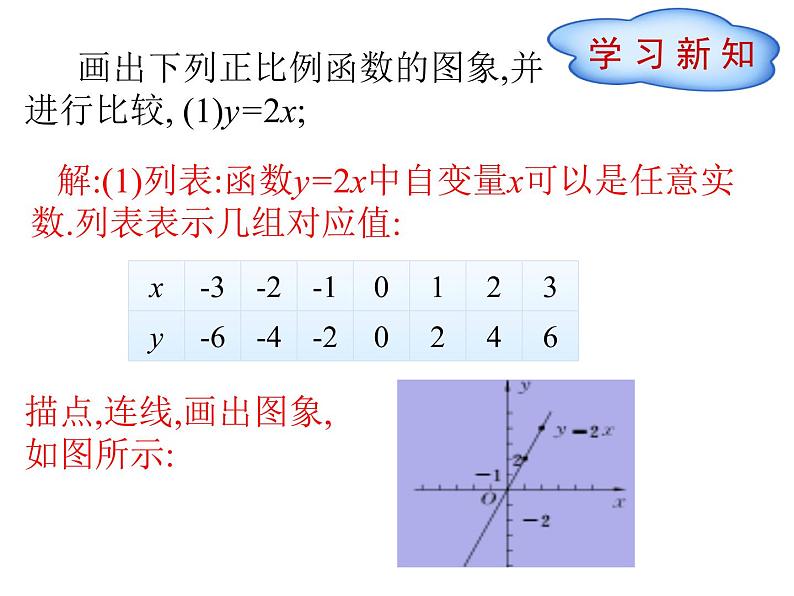
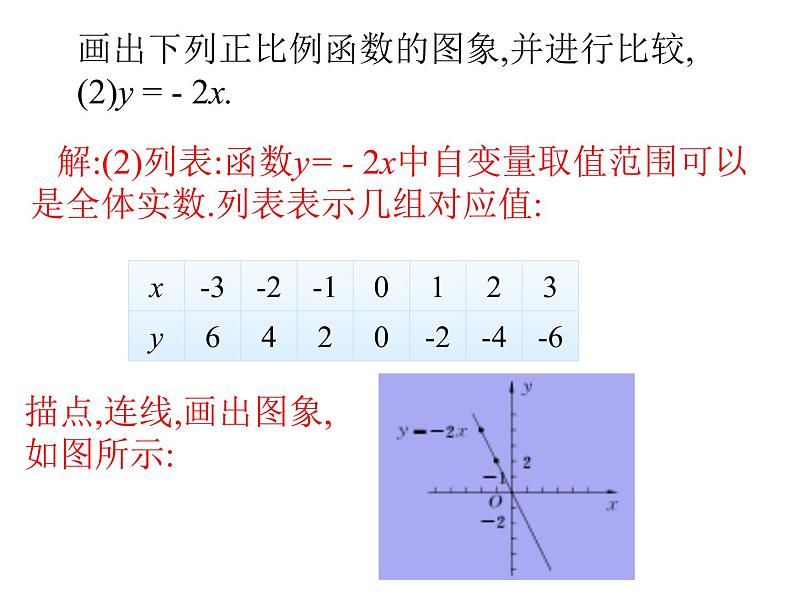
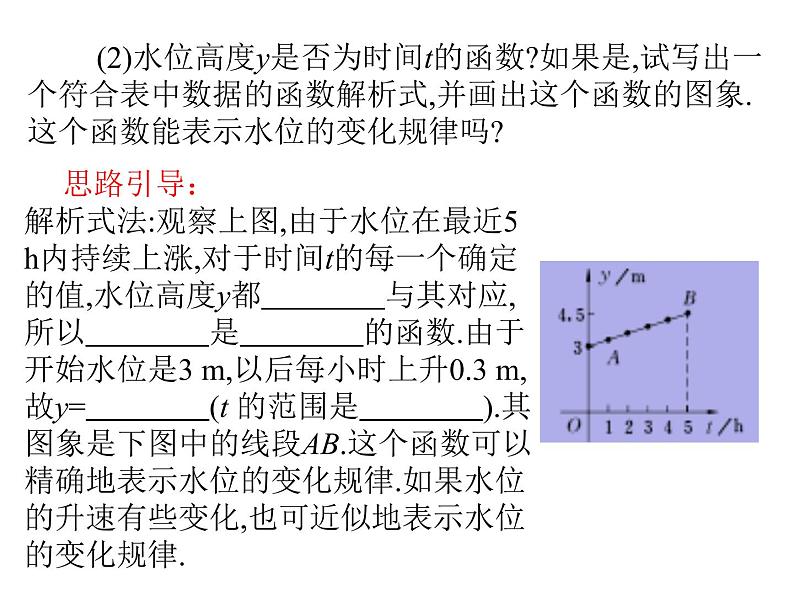
例:(教材例3)画出函数y=2x-1 与y=-0.5x+1的图象.
〔解析〕由于一次函数的图象是直线, 因 此只要确定两个点就能画出它.
过点(0,-1),(1,1)画出直线y=2x-1,过点(0,1),(1,0.5)画出直线y=-0.5x+1.
解:列表表示x=0,x=1时两个函数的对应值.
一次函数y=kx+b(k≠0)的图象可以由直线y=kx平移|b|个单位长度得到.
当b>0时,向上平移;当b<0时,向下平移.
先画出直线y=2x,再把直线y=2x向下平移1个单位长度得到直线y=2x-1;先画出直线y=-0.5x,再把直线y=-0.5x向上平移1个单位长度即可得到直线y=-0.5x+1.
例:分别画出下列函数的图象. (1)y=x+1; (2)y=2x-1; (3)y=-x+1; (4)y=-2x-1.
解析:根据一次函数图象的画法,分别确定直线上的两个点,经过这两个点即可画出函数的图象.
解:经过点(0,1),(-1,0) 画出直线y=x+1;经过点(0,-1),(1,1)画出直线y=2x-1; 经过点(0,1),(1,0)画出直线y=-x+1;经过点(0,-1),(-1,1)画出直线y=-2x-1.
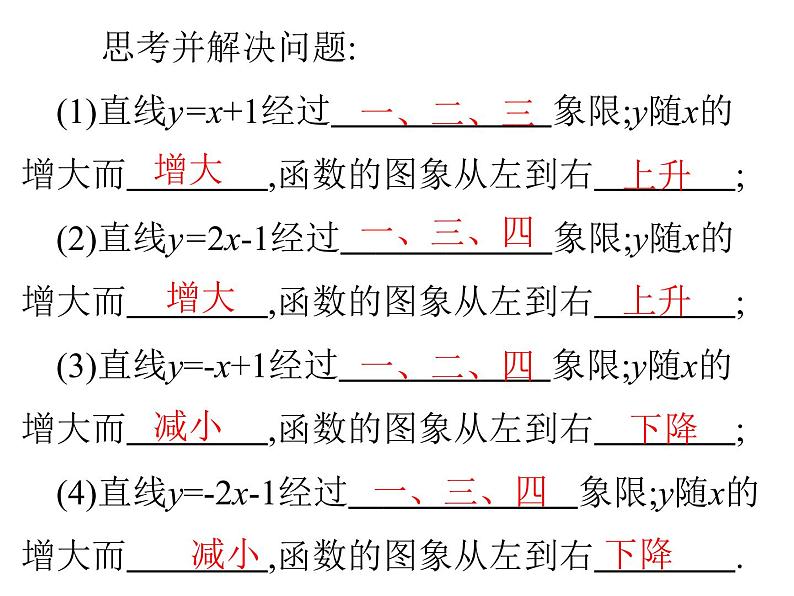
思考并解决问题: (1)直线y=x+1经过 象限;y随x的增大而 ,函数的图象从左到右 ; (2)直线y=2x-1经过 象限;y随x的增大而 ,函数的图象从左到右 ; (3)直线y=-x+1经过 象限;y随x的增大而 ,函数的图象从左到右 ; (4)直线y=-2x-1经过 象限;y随x的增大而 ,函数的图象从左到右 .
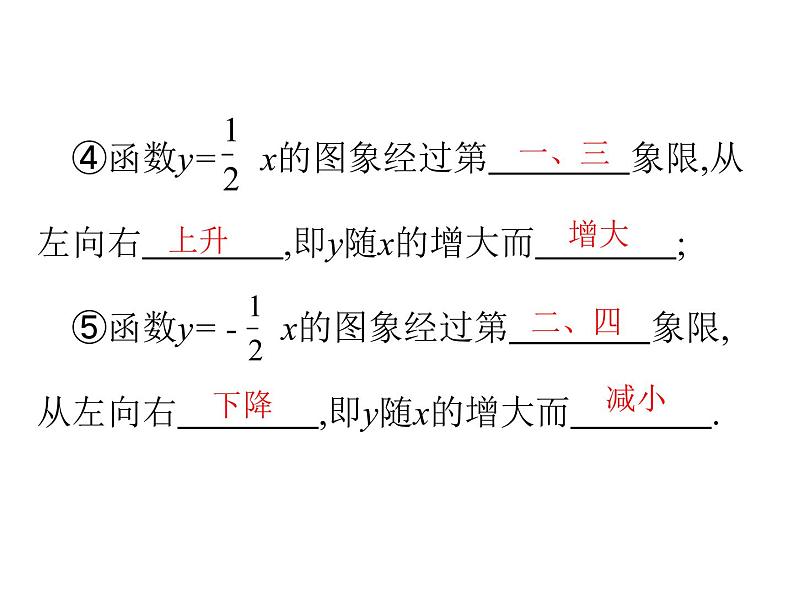
一、二、三
增大
上升
一、三、四
增大
上升
一、二、四
减小
下降
一、三、四
减小
下降
思考:
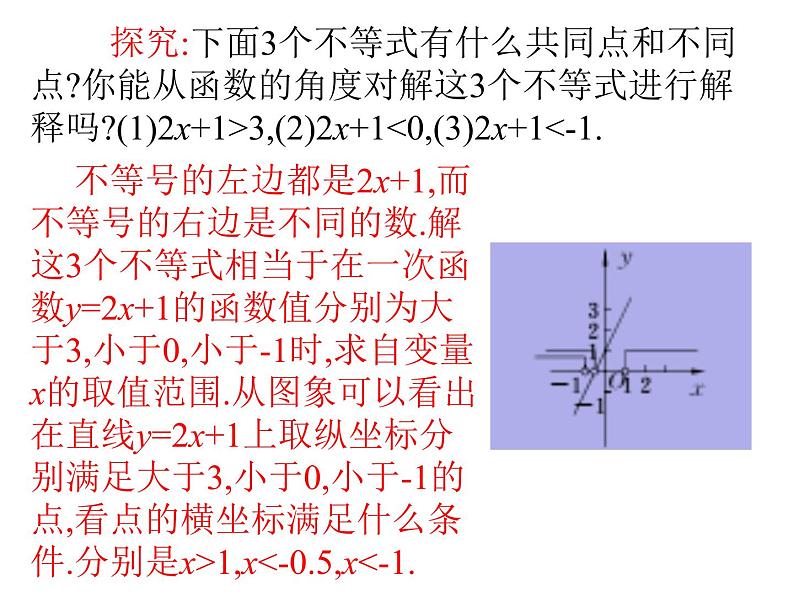
一次函数y=kx+b(k≠0)中,k的正负对函数图象有什么影响?
当k>0时,直线y=kx+b从左向右上升;当k<0时,直线y=kx+b从左向右下降.
一次函数y=kx+b(k≠0)具有如下性质:当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小.
例:(补充) 已知一次函数y=(2m-1)x-(n+3). (1)当m为何值时,y的值随x的增大而增大;
解析:y的值随x的增大而增大时,2m-1>0.
解:∵y的值随x的增大而增大, ∴2m-1>0, 解得m > .
(2)当n为何值时,此一次函数也是正比例函数;
解:由题意知n+3=0,解得n= -3.
解析:一次函数为正比例函数时,n+3=0;
(3)若m=1,n=2,写出函数解析式,求函数图象与x轴和y轴的交点坐标;画出图象,根据图象求x取什么值时,y>0?
解析:若m=1,n=2时,可确定一次函数解析式,再求函数图象与x轴、y轴的交点;再根据图象判断y>0时,x的取值范围.
解: 若m=1,n=2,则一次函数的解析式为y=x-5,令y=0,得x=5,令x=0,得y=-5,故函数图象与x轴、y轴的交点分别为(5,0),(0,-5),其函数图象如图所示.由图象知当x>5时,y>0.
知识拓展
(1)由k,b的符号可确定直线y=kx+b的位置.反过来,由直线 y=kx+b的位置也可以确定k,b的符号.不画图象,由k,b的符号 直接判定直线的位置,k的符号决定直线的倾斜方向,b的符号 决定直线与y轴交点的位置.
(2)|k|的大小决定直线的倾斜程度,即|k|越大,直线与x轴相交成 的锐角越大;|k|越小,直线与x轴相交成的锐角越小.b决定直 线与y轴交点的位置,b>0,直线与y轴的交点在y轴的正半轴 上;b<0,直线与y轴的交点在y轴的负半轴上.
(3)直线y=k1x+b1 与直线y=k2x+b2的位置关系:当k1=k2,b1=b2时, 两直线重合;当k1=k2,b1≠b2时,两直线平行;当k1≠k2,b1=b2时, 两直线相交于y轴上的一点(0,b1 );当k1≠k2,b1≠b2时,两直线 相交.
课堂小结
1.正比例函数y=kx(k≠0)的图象是经过两点(0,0),(1,k)的一条直线,一次函数y=kx+b(k≠0)的图象是经过两点(0,b), ( ,0)的一条直线,我们把这条直线称为直线y=kx+b. 具体性质如下表.
2.k,b对一次函数图象的影响:
(1)当k>0时,y随x的增大而增大, 当k<0时,y随x的增大而减小.
(2)k决定着一次函数图象的倾斜程度, |k|越大,其图象与x轴的夹角就越大.
(3)b决定着直线与y轴的交点位置,当b大于0时,交点 在y轴正半轴上;当b小于0时,交点在y轴负半轴上.
(4)直线y=kx+b可以看成是由直线y=kx平移|b|个单位 长度得到的(当b>0时,向上平移;当b<0时,向下平移).
3.一次函数的图象的画法. 由于一次函数的图象是直线,因此只要确定两个点就能画出它,一般选取直线与x轴、y轴的交点.
1.下列一次函数中y随x值的增大而减小的是( )A.y=2x+1 B.y=3-4x C.y= x+2 D.y=(5-2)x
解析:根据一次函数的性质可知:当k<0时,y随x的增大而减小,寻找k<0的一次函数即可.
B
2.y=3x与y=3x-3的图象在同一坐标系中的位置关系是 ( ) A.相交 B.互相垂直 C.平行 D.无法确定
解析:一次函数y=kx+b(k≠0)的图象可以由直线y=kx平移|b|个单位长度得到.因此,当k相同时,两条直线互相平行.故选C.
C
3.将直线y= x+3向 平移 个单位长度可得到直线y= x-2.
下
解析:直线y= x+3可以看作是由直线y= x向上平移3个单位长度得到的,直线y= x-2可以看作是由直线y= x向下平移2个单位长度得到的.因此,将直线y= x+3向下平移5个单位长度可得到直线y= x-2.
5
4.若一次函数y=(1-2m)x+3的图象经过A(x1,y1),B(x2,y2)两点.当x1y2,则m的取值范围是什么?
解:由x1y2可知y随x的增大而减小, 因此1-2m<0,解得m > .
八年级数学·下 新课标[人]
第十九章 一次函数
19.2.2 一次函数(第2课时)
想一想
正比例函数与一次函数有何关系?
一次函数y=kx+b(k≠0),当b=0时,一次函数则为正比例函数y=kx,因此,正比例函数是当常数项b=0时的一次函数,是特殊的一次函数.
例:(教材例3)画出函数y=2x-1 与y=-0.5x+1的图象.
〔解析〕由于一次函数的图象是直线, 因 此只要确定两个点就能画出它.
过点(0,-1),(1,1)画出直线y=2x-1,过点(0,1),(1,0.5)画出直线y=-0.5x+1.
解:列表表示x=0,x=1时两个函数的对应值.
一次函数y=kx+b(k≠0)的图象可以由直线y=kx平移|b|个单位长度得到.
当b>0时,向上平移;当b<0时,向下平移.
先画出直线y=2x,再把直线y=2x向下平移1个单位长度得到直线y=2x-1;先画出直线y=-0.5x,再把直线y=-0.5x向上平移1个单位长度即可得到直线y=-0.5x+1.
例:分别画出下列函数的图象. (1)y=x+1; (2)y=2x-1; (3)y=-x+1; (4)y=-2x-1.
解析:根据一次函数图象的画法,分别确定直线上的两个点,经过这两个点即可画出函数的图象.
解:经过点(0,1),(-1,0) 画出直线y=x+1;经过点(0,-1),(1,1)画出直线y=2x-1; 经过点(0,1),(1,0)画出直线y=-x+1;经过点(0,-1),(-1,1)画出直线y=-2x-1.
思考并解决问题: (1)直线y=x+1经过 象限;y随x的增大而 ,函数的图象从左到右 ; (2)直线y=2x-1经过 象限;y随x的增大而 ,函数的图象从左到右 ; (3)直线y=-x+1经过 象限;y随x的增大而 ,函数的图象从左到右 ; (4)直线y=-2x-1经过 象限;y随x的增大而 ,函数的图象从左到右 .
一、二、三
增大
上升
一、三、四
增大
上升
一、二、四
减小
下降
一、三、四
减小
下降
思考:
一次函数y=kx+b(k≠0)中,k的正负对函数图象有什么影响?
当k>0时,直线y=kx+b从左向右上升;当k<0时,直线y=kx+b从左向右下降.
一次函数y=kx+b(k≠0)具有如下性质:当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小.
例:(补充) 已知一次函数y=(2m-1)x-(n+3). (1)当m为何值时,y的值随x的增大而增大;
解析:y的值随x的增大而增大时,2m-1>0.
解:∵y的值随x的增大而增大, ∴2m-1>0, 解得m > .
(2)当n为何值时,此一次函数也是正比例函数;
解:由题意知n+3=0,解得n= -3.
解析:一次函数为正比例函数时,n+3=0;
(3)若m=1,n=2,写出函数解析式,求函数图象与x轴和y轴的交点坐标;画出图象,根据图象求x取什么值时,y>0?
解析:若m=1,n=2时,可确定一次函数解析式,再求函数图象与x轴、y轴的交点;再根据图象判断y>0时,x的取值范围.
解: 若m=1,n=2,则一次函数的解析式为y=x-5,令y=0,得x=5,令x=0,得y=-5,故函数图象与x轴、y轴的交点分别为(5,0),(0,-5),其函数图象如图所示.由图象知当x>5时,y>0.
知识拓展
(1)由k,b的符号可确定直线y=kx+b的位置.反过来,由直线 y=kx+b的位置也可以确定k,b的符号.不画图象,由k,b的符号 直接判定直线的位置,k的符号决定直线的倾斜方向,b的符号 决定直线与y轴交点的位置.
(2)|k|的大小决定直线的倾斜程度,即|k|越大,直线与x轴相交成 的锐角越大;|k|越小,直线与x轴相交成的锐角越小.b决定直 线与y轴交点的位置,b>0,直线与y轴的交点在y轴的正半轴 上;b<0,直线与y轴的交点在y轴的负半轴上.
(3)直线y=k1x+b1 与直线y=k2x+b2的位置关系:当k1=k2,b1=b2时, 两直线重合;当k1=k2,b1≠b2时,两直线平行;当k1≠k2,b1=b2时, 两直线相交于y轴上的一点(0,b1 );当k1≠k2,b1≠b2时,两直线 相交.
课堂小结
1.正比例函数y=kx(k≠0)的图象是经过两点(0,0),(1,k)的一条直线,一次函数y=kx+b(k≠0)的图象是经过两点(0,b), ( ,0)的一条直线,我们把这条直线称为直线y=kx+b. 具体性质如下表.
2.k,b对一次函数图象的影响:
(1)当k>0时,y随x的增大而增大, 当k<0时,y随x的增大而减小.
(2)k决定着一次函数图象的倾斜程度, |k|越大,其图象与x轴的夹角就越大.
(3)b决定着直线与y轴的交点位置,当b大于0时,交点 在y轴正半轴上;当b小于0时,交点在y轴负半轴上.
(4)直线y=kx+b可以看成是由直线y=kx平移|b|个单位 长度得到的(当b>0时,向上平移;当b<0时,向下平移).
3.一次函数的图象的画法. 由于一次函数的图象是直线,因此只要确定两个点就能画出它,一般选取直线与x轴、y轴的交点.
1.下列一次函数中y随x值的增大而减小的是( )A.y=2x+1 B.y=3-4x C.y= x+2 D.y=(5-2)x
解析:根据一次函数的性质可知:当k<0时,y随x的增大而减小,寻找k<0的一次函数即可.
B
2.y=3x与y=3x-3的图象在同一坐标系中的位置关系是 ( ) A.相交 B.互相垂直 C.平行 D.无法确定
解析:一次函数y=kx+b(k≠0)的图象可以由直线y=kx平移|b|个单位长度得到.因此,当k相同时,两条直线互相平行.故选C.
C
3.将直线y= x+3向 平移 个单位长度可得到直线y= x-2.
下
解析:直线y= x+3可以看作是由直线y= x向上平移3个单位长度得到的,直线y= x-2可以看作是由直线y= x向下平移2个单位长度得到的.因此,将直线y= x+3向下平移5个单位长度可得到直线y= x-2.
5
4.若一次函数y=(1-2m)x+3的图象经过A(x1,y1),B(x2,y2)两点.当x1
解:由x1
相关资料
更多









