
河南省商丘市梁园区2022届九年级中考数学模拟试题 word,含答案
展开河南省商丘市梁园区2022届九年级中考数学模拟试题
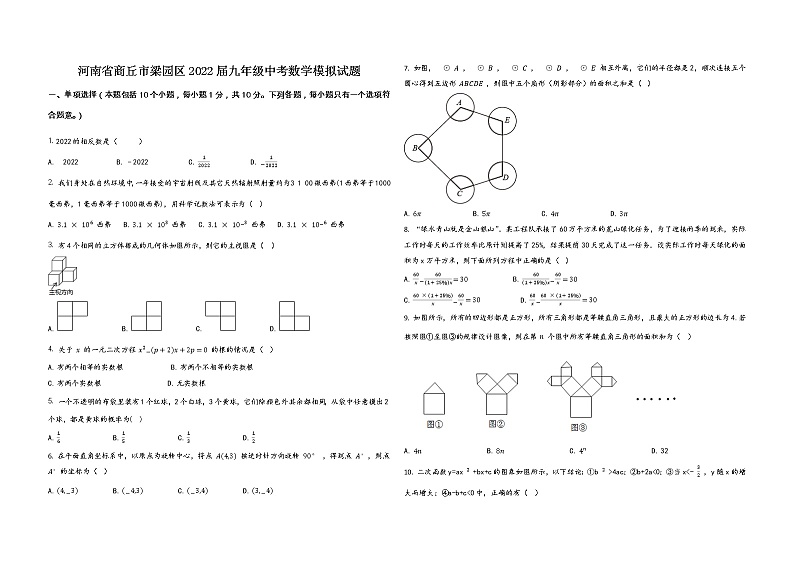
一、单项选择(本题包括10个小题,每小题1分,共10分。下列各题,每小题只有一个选项符合题意。)
1. 2022的相反数是( )
A. 2022 B. ﹣2022 C. D.
2. 我们身处在自然环境中,一年接受的宇宙射线及其它天然辐射照射量约为3 1 00微西弗(1西弗等于1000毫西弗,1毫西弗等于1000微西弗),用科学记数法可表示为( )
A. 西弗 B. 西弗 C. 西弗 D. 西弗
3. 有4个相同的立方体搭成的几何体如图所示,则它的主视图是( )
A. B. C. D.
4. 关于 的一元二次方程 的根的情况是( )
A. 有两个相等的实数根 B. 有两个不相等的实数根
C. 有两个实数根 D. 无实数根
5. 一个不透明的布袋里装有1个红球,2个白球,3个黄球,它们除颜色外其余都相同,从袋中任意摸出2个球,都是黄球的概率为( )
A. B. C. D.
6. 在平面直角坐标系中,以原点为旋转中心,将点 按逆时针方向旋转 ,得到点 ,则点 的坐标为( )
A. B. C. D.
7. 如图, , , , , 相互外离,它们的半径都是2,顺次连接五个圆心得到五边形 ,则图中五个扇形(阴影部分)的面积之和是( )
A. B. C. D.
8. “绿水青山就是金山银山”.某工程队承接了60万平方米的荒山绿化任务,为了迎接雨季的到来,实际工作时每天的工作效率比原计划提高了25%,结果提前30天完成了这一任务.设实际工作时每天绿化的面积为x万平方米,则下面所列方程中正确的是( )
A. B.
C. D.
9. 如图所示,所有的四边形都是正方形,所有三角形都是等腰直角三角形,且最大的正方形的边长为4.若按照图①至图③的规律设计图案,则在第 个图中所有等腰直角三角形的面积和为( )
A. B. C. D. 32
10. 二次函数y=ax +bx+c的图象如图所示,以下结论:①b >4ac;②b+2a<0;③当x<- ,y随x的增大而增大;④a-b+c<0中,正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
二.填空题(共5题,总计16分)
11. 请写出一个比 小的正整数 .
12. 不等式组 的解集为________.
13. 一个不透明的袋子中装有3个红球,2个白球,小球除颜色外其他均相同,若同时从袋子中任取2个小球,则恰为一个红球,一个白球的概率为________
14. .如图,AB是半圆O的直径,且AB=8,点C为半圆上的一点.将此半圆沿BC所在的直线折叠,若圆弧BC恰好过圆心O,则图中阴影部分的面积是________.(结果保留π)
15. 如图,在Rt△ABC中,AC=8,BC=6,点D为斜边AB上一点,DE⊥AB交AC于点E,将△AED沿DE翻折,点A的对应点为点F.如果△EFC是直角三角形,那么AD的长为 .
三.解答题(共4题,总计10分)
16. (1).解不等式组:
请结合题意填空,完成本题的解答
(I)解不等式①,得 ▲ ;
(Ⅱ)解不等式②,得 ▲ ;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
(Ⅳ)原不等式组的解集为 ▲ .
(2).解方程: .
17. 小手拉大手,共创文明城.某校为了了解家长对南宁市创建全国文明城市相关知识的知晓情况,通过发放问卷进行测评,从中随机抽取 份答卷,并统计成绩(成绩得分用 表示,单位:分),收集数据如下:
整理数据:
|
|
|
|
|
|
|
|
分析数据:
平均分 | 中位数 | 众数 |
|
|
|
根据以上信息,解答下列问题:
(1)直接写出上述表格中 的值;
(2)该校有 名家长参加了此次问卷测评活动,请估计成绩不低于 分的人数是多少?
(3)请从中位数和众数中选择一个量, 结合本题解释它的意义.
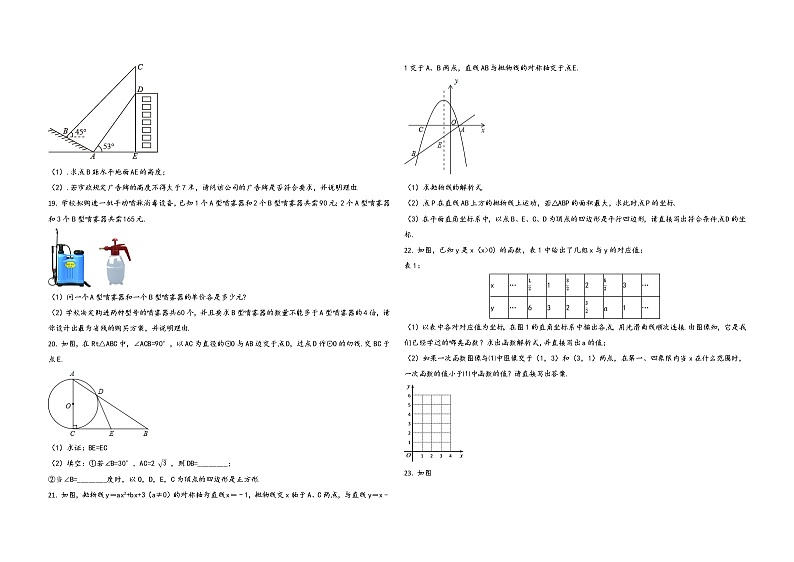
18. 教育部颁布的《基础教育课程改革纲要》要求每位学生每学年都要参加社会实践活动,某学校组织了一次测量探究活动,如图,某大楼的顶部竖有一块广告牌CD,小明与同学们在山坡的坡脚A处测得广告牌底部D的仰角为53°,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度 , 米, 米(测角器的高度忽略不计,结果精确到0.1米,参考数据: , , , , )
(1).求点B距水平地面AE的高度;
(2).若市政规定广告牌的高度不得大于7米,请问该公司的广告牌是否符合要求,并说明理由.
19. 学校拟购进一批手动喷淋消毒设备,已知1个A型喷雾器和2个B型喷雾器共需90元;2个A型喷雾器和3个B型喷雾器共需165元.
(1)问一个A型喷雾器和一个B型喷雾器的单价各是多少元?
(2)学校决定购进两种型号的喷雾器共60个,并且要求B型喷雾器的数量不能多于A型喷雾器的4倍,请你设计出最为省钱的购买方案,并说明理由.
20. 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线.交BC于点E.
(1)求证:BE=EC
(2)填空:①若∠B=30°,AC=2 ,则DB=________;
②当∠B=________度时,以O,D,E,C为顶点的四边形是正方形.
21. 如图,抛物线y=ax2+bx+3(a≠0)的对称轴为直线x=﹣1,抛物线交x轴于A、C两点,与直线y=x﹣1交于A、B两点,直线AB与抛物线的对称轴交于点E.
(1)求抛物线的解析式.
(2)点P在直线AB上方的抛物线上运动,若△ABP的面积最大,求此时点P的坐标.
(3)在平面直角坐标系中,以点B、E、C、D为顶点的四边形是平行四边形,请直接写出符合条件点D的坐标.
22. 如图,已知y是x(x>0)的函数,表1中给出了几组x与y的对应值:
表1:
x | … |
| 1 |
| 2 |
| 3 | … |
y | … | 6 | 3 | 2 |
|
| 1 | … |
(1)以表中各对对应值为坐标,在图1的直角坐标系中描出各点,用光滑曲线顺次连接.由图像知,它是我们已经学过的哪类函数?求出函数解析式,并直接写出a的值;
(2)如果一次函数图像与⑴中图像交于(1,3)和(3,1)两点,在第一、四象限内当x在什么范围时,一次函数的值小于⑴中函数的值?请直接写出答案.
23. 如图
(1).(问题背景)如图1,在 中, , ,D是直线BC上的一点,将线段AD绕点A逆时针旋转90°至AE,连接CE,求证: ;
(2).(尝试应用)如图2,在(1)的条件下,延长DE,AC交于点G, 交DE于点F.求证: ;
(3).(拓展创新)如图3, 是 内一点, , , ,直接写出 的面积为 .
参考答案
一.选择题
1. B 2. C 3. D 4. C 5. B 6. C 7. A 8. C 9. A 10. C
二. 填空题
11. 1或2
12. ≤
13.
14.
15. 或5
三. 解答题
16. (1)解:(I)x≥-2;(Ⅱ)x<3;(Ⅲ)在数轴上表示结果如下:
;
(Ⅳ)-2≤x<3
(2)解:
解:
检验:当 时, ,所以原分式方程的解是 .
17. (1)a=20-3-4-8=5;
将这组数据按大小顺序排列为:
81,82,83,86,87,88,89,90,90,90,92,93,96,96,98,99,100,100,100,100,
其中第10个和第11个数据分别是90,92,
所以,这组数据的中位数b= ;
100出现了4次,出现的次数最多,所以,众数c是100;
(2) ,
(人)
(3)中位数:在统计的问卷的成绩中,最中间的两个分数的平均数是91分;
众数:在统计的问卷的成绩中,得 分的人数最多.
18. (1)解:过 作 于G, 于H,
中, ,
∴ ,
∴ 米
∴点 距水平地面 的距离为5米.
(2)解:由(1)得: , ,
∵ 于G, 于H,∠AED=90°,
∴四边形BHEG是矩形,
∴BG=HE
即 ,
在 中, ,
∴ .
在 中, , ,
∴ .
∴ .
答:广告牌CD高符合要求.
19. (1)解:设一个A型喷雾器的单价为 元,一个B型喷雾器的单价为 元,由题意可得:
解之得: ,
答:一个A型喷雾器的单价为60元,一个B型喷雾器的单价为15元;
(2)解:设购进A型喷雾器 个,则购进B型喷雾器 个,由题意可得:
≤
解之得: ≥12
设购买这些喷雾器的总费用为W元,则有:
∵
∴W随 的增大而增大
∴当 时,W取得最小值,及最省钱.
(个)
答:最省钱的购买方案为:购买A型喷雾器12个,B型喷雾器48个.
20. (1)证明:连接DO.
∵∠ACB=90°,AC为直径,
∴EC为⊙O的切线;
又∵ED也为⊙O的切线,
∴EC=ED,
又∵∠EDO=90°,
∴∠BDE+∠ADO=90°,
∴∠BDE+∠A=90°
又∵∠B+∠A=90°,
∴∠BDE=∠B,
∴BE=ED,
∴BE=EC
(2)解:①∵∠ACB=90°,∠B=30°,AC=2 ,
∴AB=2AC=4 ,
∴BC= =6,
∵AC为直径,
∴∠BDC=∠ADC=90°,
由(1)得:BE=EC,
∴DE= BC=3,
故答案为:3;
②当∠B=45°时,四边形ODEC是正方形,理由如下:
∵∠ACB=90°,
∴∠A=45°,
∵OA=OD,
∴∠ADO=45°,
∴∠AOD=90°,
∴∠DOC=90°,
∵∠ODE=90°,
∴四边形DECO是矩形,
∵OD=OC,
∴矩形DECO是正方形.
故答案为:45.
21. (1)解:令y=0,可得:x﹣1=0,解得:x=1,
∴点A(1,0),
∵抛物线y=ax2+bx+3(a≠0)的对称轴为直线x=﹣1,
∴﹣1×2﹣1=﹣3,即点C(﹣3,0),
∴ ,解得:
∴抛物线的解析式为:y=﹣x2﹣2x+3
(2)解:∵点P在直线AB上方的抛物线上运动,
∴设点P(m,﹣m2﹣2m+3),
∵抛物线与直线y=x﹣1交于A、B两点,
∴ ,解得: ,
∴点B(﹣4,﹣5),
如图,过点P作PF∥y轴交直线AB于点F,
则点F(m,m﹣1),
∴PF=﹣m2﹣2m+3﹣m+1=﹣m2﹣3m+4,
∴S△ABP=S△PBF+S△PFA
= (﹣m2﹣3m+4)(m+4)+ (﹣m2﹣3m+4)(1﹣m)
=- (m+ )2+ ,
∴当m= 时,P最大,
∴点P( , ).
(3)当x=﹣1时,y=﹣1﹣1=﹣2,
∴点E(﹣1,﹣2),
如图,直线BC的解析式为y=5x+15,直线BE的解析式为y=x﹣1,直线CE的解析式为y=﹣x﹣3,
∵以点B、C、E、D为顶点的四边形是平行四边形,
∴直线D1D3的解析式为y=5x+3,直线D1D2的解析式为y=x+3,直线D2D3的解析式为y=﹣x﹣9,
联立 得D1(0,3),
同理可得D2(﹣6,﹣3),D3(﹣2,﹣7),
综上所述,符合条件的点D的坐标为D1(0,3),D2(﹣6,﹣3),D3(﹣2,﹣7).
22. (1)解:函数图像如下:
这是反比例函数,
设解析式为 ,将 代入可得: ,
即函数解析式为: ;
将x= 代入可得
(2)解:因为一次函数图像与⑴中图像交于(1,3)和(3,1)两点
所以当
或 时,一次函数的值小于⑴中函数的值.
23. (1)证明:如图1,
∵ ,
∴ ,
在 和 中,
,
∴
(2)证明:如图2,过点D作 交FB的延长线于K.
∵ , ,
∴ ,
∵ , ,
∴ ,
∴ ,
∴ ,
∵ ,
∴ , ,
∴ ,
∵ , ,
∴ ,
∴ ,
在 和 中,
,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,即 .
(3)【拓展创新】如图3中,过点A作 交BD于E,连接CE.
∵ , ,
∴ 与 都是等腰直角三角形,
同法可证 ,
∴ ,
∵ ,
∴ ,
∴ .
河南省商丘市梁园区2023-2024学年九年级上学期期末数学试题: 这是一份河南省商丘市梁园区2023-2024学年九年级上学期期末数学试题,共26页。试卷主要包含了试卷上不要答题,请用0等内容,欢迎下载使用。
+河南省商丘市梁园区2023--2024学年九年级上学期期末数学试题+: 这是一份+河南省商丘市梁园区2023--2024学年九年级上学期期末数学试题+,共10页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
河南省商丘市梁园区2023-2024学年七年级上学期1月月考数学模拟试题(含答案): 这是一份河南省商丘市梁园区2023-2024学年七年级上学期1月月考数学模拟试题(含答案),共6页。












