初中数学23.2.1 中心对称课文课件ppt

人教版九年级上册

 23.2.1 中心对称

同步练习

一、选择题(每题5分)

1、下列图形中旋转180°后不能与自身重合的图形的是(    )

A   等边三角形                  B  平行四边形

C   矩形                        D  菱形

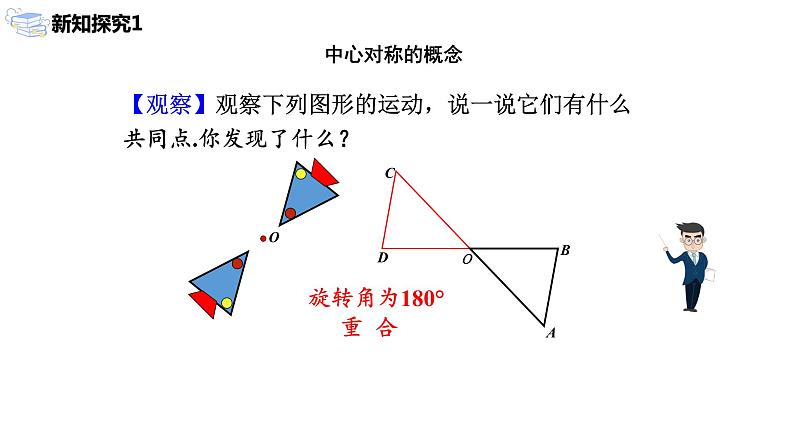
2、已知下列命题：

⑴关于中心对称的两个图形一定不全等

⑵关于中心对称的两个图形是全等形

⑶两个全等的图形一定关于中心对称

其中真命题的个数是                        （  ）

A、0            B、1           C、2             D、3

3、如图，旋转180°后不能与自身重合的图形的是（  ）

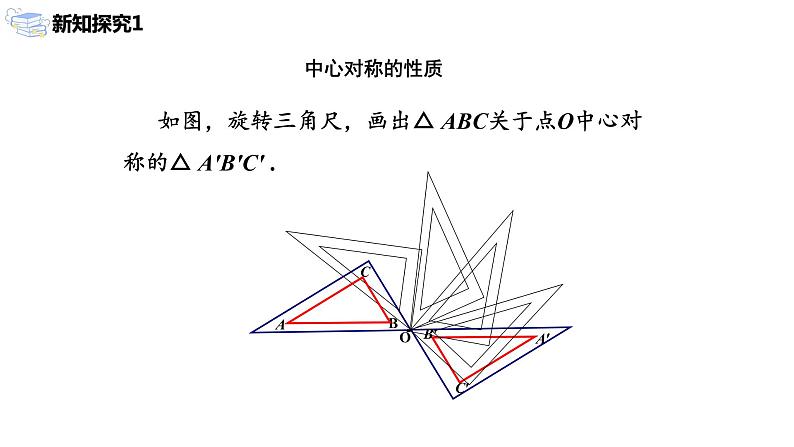
4、△ABC和△AˊBˊCˊ关于点O对称，下列结论不正确的是（      ）

A    AO=AˊO                   B   AB∥AˊBˊ

C    CO=BO                     D   ∠BAC=∠BˊAˊCˊ

5、下列说法中正确的是(       )

A可以重合的两个图形一定是轴对称

B可以重合的两个图形一定是中心对称

C两个成中心对称的图形的对称点连线必过对称中心

D两个可以重合的三角形一定关于某一点成中心对称

二、填空题(每题5分)

6、关于中心对称的两个图形，对称点的连线经过___________，并被________平分；

7、关于中心对称的两个图形对应线段____________；

8、线段、两相交直线、角、等腰三角形、等边三角形、平行四边形、矩形、菱形、正方形、圆等图形中旋转180°后能与自身重合的图形的有：                         ；

9、关于点O成中心对称的两个四边形ABCD和EFGH，AD、BE、CF、DG都过      ；并被点_______所________，AB∥___，BC∥____，EF∥____，FG∥_________；

10、若点O是平行四边形ABCD对角线AC的中点，EF⊥AC于O交AD、BC分别于E、F，那么线段DE关于点O的对称线段是_____________。

三、判断题(每题5分)

11、两个能够重合的图形一定是中心对称；       （        ）

12、轴对称图形也是中心对称图形；               （        ）

13、对顶角是中心对称图形；                     （        ）

四、解答题(25分)

14、如图，已知△ABC及点P，求作△DEF，使△DEF与△ABC关于点P对称。

人教版九年级上册

 23.2.1 中心对称

同步练习答案

一、选择题(每题5分)

1、下列图形中旋转180°后不能与自身重合的图形的是(    )

A   等边三角形                  B  平行四边形

C   矩形                        D  菱形

【答案】A

【解析】

试题分析：平行四边形、矩形、菱形的对称线都互相平分，它们旋转180°后都能与自身重合，只有等边三角形旋转180°后不能与自身重合.

故应选A.

考点：图形的旋转

2、已知下列命题：

⑴关于中心对称的两个图形一定不全等

⑵关于中心对称的两个图形是全等形

⑶两个全等的图形一定关于中心对称

其中真命题的个数是                        （  ）

A、0            B、1           C、2             D、3

【答案】B

【解析】

试题分析：⑴关于中心对称的两个图形可以完全重合，所以一定全等，故(1)错误；

⑵关于中心对称的两个图形可以完全重合，所以一定全等，故(2)正确；

⑶两个图形全等不一定关于某点中心对称，故(3)错误.

所以正确的只有1个.

故应选B.

考点：中心对称的性质.

3、如图，旋转180°后不能与自身重合的图形的是（  ）

【答案】B

【解析】

试题分析：A、C、D选项的图形中花瓣的数量是偶数，所以旋转180°后能与自身重合，只有B选项中的图形花瓣的数量是奇数，所以旋转180°后不能与自身重合,

故应选B

考点：图形的旋转.

4、△ABC和△AˊBˊCˊ关于点O对称，下列结论不正确的是（      ）

A    AO=AˊO                   B   AB∥AˊBˊ

C    CO=BO                     D   ∠BAC=∠BˊAˊCˊ

【答案】C

【解析】

试题分析：因为△ABC和△AˊBˊCˊ关于点O对称，所以△ABC和△AˊBˊCˊ的对应边相等且平行

对应角相等，对称点的连线经过对称中心，且被对称中心平分，所以可得AO=AˊO、AB∥AˊBˊ、∠BAC=∠BˊAˊCˊ，因为点C与点B不是对点，所以BO与CO不一定相等.

故应选C.

考点：中心对称的性质.

5、下列说法中正确的是(       )

A可以重合的两个图形一定是轴对称

B可以重合的两个图形一定是中心对称

C两个成中心对称的图形的对称点连线必过对称中心

D两个可以重合的三角形一定关于某一点成中心对称

【答案】C

【解析】

试题分析：A选项，可以重合的图形可能是经过平移或旋转重合的，所以不一定是轴对称，故A选项错误；

B选项，可以重合的图形可能是经过平移或翻折重合的，所以不一定是中心称，故B选项错误；

C选项，根据中心对称的性质可知：两个成中心对称的图形的对称点连接必经过对称中心，故C选项正确；

D选项，两个三角形可以重合可能是经过平移或翻折重合的，不一定是中心对称的关系，故D选项错误.

故应选C.

考点：

二、填空题(每题5分)

6、关于中心对称的两个图形，对称点的连线经过___________，并被________平分；

【答案】对称中心；对称中心

【解析】

试题分析：根据中心对称的性质可得：关于中心对称的两个图形，对称点的连线经过对称中心，并被对称中心平分.

考点：中心对称的性质.

7、关于中心对称的两个图形对应线段____________；

【答案】相等

【解析】

试题分析：关于中心对称的两个图形可以完全重合，所以对应线段相等.

考点：中心对称的性质.

8、线段、两相交直线、角、等腰三角形、等边三角形、平行四边形、矩形、菱形、正方形、圆等图形中旋转180°后能与自身重合的图形的有：                         ；

【答案】线段、两相交直线、平行四边形、矩形、菱形、正方形、圆.

【解析】

试题分析：旋转180°后能与自身重合的图形有：线段、两相交直线、平行四边形、矩形、菱形、正方形、圆.

考点：中心对称

9、关于点O成中心对称的两个四边形ABCD和EFGH，AD、BE、CF、DG都过      ；并被点_______所________，AB∥___，BC∥____，EF∥____，FG∥_________；

【答案】O；O，EF；FG；AB；BC.

【解析】

试题分析：根据关于中心对称的两个图形的对称点的连线都经过对称中心，所以AD、BE、CF、DG都经过点O；根据关于中心对称的两个图形的对应边相等且互相平行可得：AB∥EF、BC∥FG、EF∥AB、FG∥BC.

考点：中心对称的性质.

10、若点O是平行四边形ABCD对角线AC的中点，EF⊥AC于O交AD、BC分别于E、F，那么线段DE关于点O的对称线段是_____________。

【答案】BF

【解析】

试题分析：根据题意画出图形，再根据中心对称的性质找到点D、E的对称点，从而得到线段DE关于点O的对称线段.

解：作图如下，

因为平行四边形ABCD绕点O旋转180°后能与自身重合，

所以平行四边形ABCD绕点O旋转180°点D与点B重合，点E与点F重合，

所以DE关于点O的对称线段是BF.

考点：中心对称

三、判断题(每题5分)

11、两个能够重合的图形一定是中心对称；       （        ）

【答案】×

【解析】

试题分析：关于某点中心对称的两个图形一定能重合，能重合的两个图形不一定是中心对称关系.

故错误；

考点：中心对称

12、轴对称图形也是中心对称图形；               （        ）

【答案】×

【解析】

试题分析：关于某条直线轴对称的图形不一定是中心对称图形.

故错误.

考点：轴对称图形

13、对顶角是中心对称图形；                     （        ）

【答案】√

【解析】

试题分析：因为对顶角是两条直线相交形成的，而两条相交直线组成的图形是中心对称图形.

故正确.

考点：中心对称图形.

四、解答题(25分)

14、如图，已知△ABC及点P，求作△DEF，使△DEF与△ABC关于点P对称。

【答案】作图见解析

【解析】

试题分析：根据中心对称的性质分别连接AP、BP、CP，并延长使AP=DP、BP=EP、CP=FP，再顺次连接D、E、F得到△DEF与△ABC关于点P对称。

解：作图如下，

考点：