人教版九年级上册23.2.1 中心对称课文课件ppt

这是一份人教版九年级上册23.2.1 中心对称课文课件ppt，共29页。PPT课件主要包含了新课导入，讲授新课，问题一，问题二，当堂练习，课堂小结等内容，欢迎下载使用。

1．认识两个图形关于某一点中心对称的本质．2．理解中心对称的性质，并可以判断两个图形是否成中心对称．3．会画某图形关于某点对称的图形，会确定对称中心．
中心对称的概念和性质.
掌握中心对称的性质及其应用.
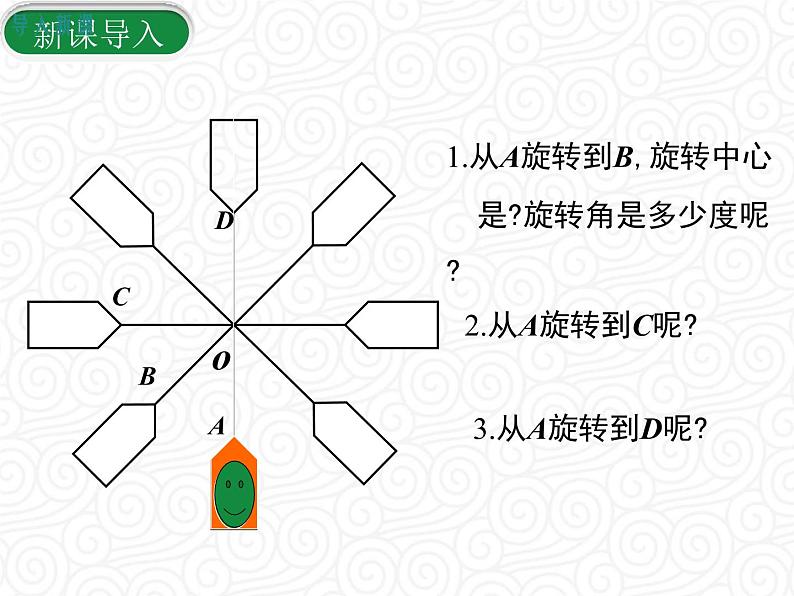
1.从A旋转到B,旋转中心 是?旋转角是多少度呢?
(1)如图，把其中一个图案绕点O 旋转180°，你有什 么发现？ 两个图案能够完全重合在一起．
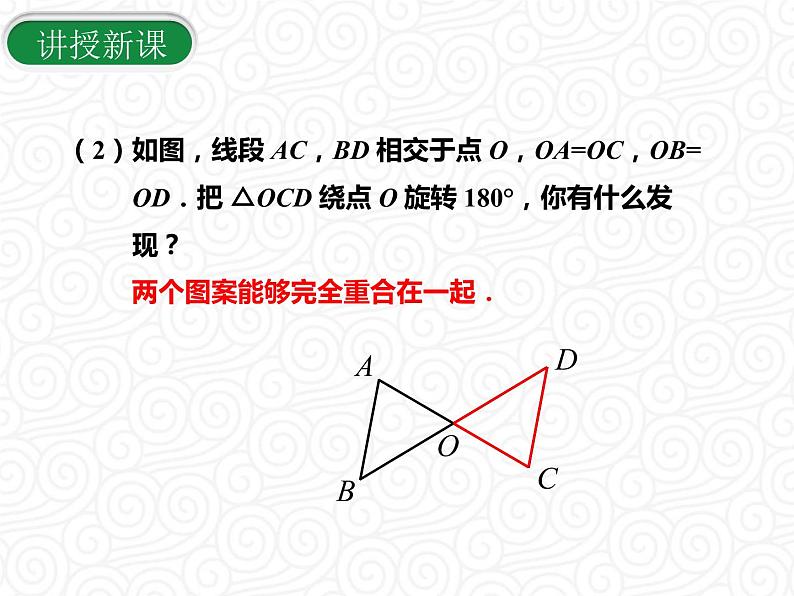
（2）如图，线段 AC，BD 相交于点 O，OA=OC，OB= OD．把 △OCD 绕点 O 旋转 180°，你有什么发 现？ 两个图案能够完全重合在一起．
你能说说上述两个旋转的共同点吗？（1）图形中旋转中心是哪一点？（2）旋转的角度是多少？（3）两个图形的关系？（1）点 O（2）180°（3）重合
把一个图形 ，如果它 ，那么就说这两个图形关于这个点 或 ，这个点叫做 . 这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点.
绕着某一点旋转180°
【思考】两个图形成中心对称需要具备什么条件？
两个图形成中心对称须具备三个条件：①能找到一个对称中心；②旋转角为180°；③这两个图形旋转后能重合.
如图，△OCD与△OAB关于点O中心对称 ，则____是对称中心，点A与_____是对称点， 点B与____是对称点.
如图，旋转三角尺，画出△ABC关于点O中心对称的△A′B′C′ .
下图中△A′B′C′与△ABC关于点O是成中心对称,你能从图中找到哪些等量关系?
(1) OA=OA′、OB=OB′、 OC=OC′
（2）△ABC≌△A′B′C′

1.成中心对称的两个图形中，对应点所连线段经过对称中心，且被对称中心平分.（即对称点与对称中心三点共线）
2.中心对称的两个图形是全等形.
如图，△A′B′C′与△ABC关于点O成中心对称，你能从图 中找出哪些相等的线段、相等的角、全等的三角形以及有 特殊位置关系的线段？ 导引：根据中心对称的性质可知：如果两个图形关于某点成中心对 称，那么对称点所连线段都经过对称中心而且被对称中心平 分，而且这两个图形是全等图形，对应边平行(或共线)且相等． 解：可以找到：OA＝OA′，OB＝OB′，OC＝OC′，△ABC≌ △A′B′C′，AB A′B′，AC A′C′，BC B′C′， ∠BAC＝∠B′A′C′，∠ABC＝∠A′B′C′，∠ACB＝ ∠A′C′B′等．
如图，已知四边形ABCD和点O，试画出四边形ABCD关于点O成中心对称的图形A'B'C'D'.
分析：要画出四边形ABCD关于点O成中心对称的图形，只要画出A，B，C，D四点关于点O的对称点，再顺次连接各对应点即可.
1.连接AO并延长到A'，使OA'=OA，得到点A的对应点A'；
2.同理，可作出点B，C，D的对应点B'，C'，D'；
3.顺次连接A'，B'，C'，D'，则四边形A'B'C'D'即为所作.
如图，已知△ABC与△A′B′C′中心对称，找出它们的对称中心O.
解法1：根据观察，B、B′应是对应点，连接BB′，用刻度尺找出BB′的中点O，则点O即为所求（如图）.
解法2：根据观察，B、B′及C、C′应是两组对应点，连接BB′、CC′，BB′、CC′相交于点O，则点O即为所求（如图）.
注意：如果限制只用直尺作图，我们用解法2.
如图，已知△AOB与△DOC成中心对称，△AOB的面积是12，AB＝3，则△DOC中CD边上的高为________.
解析：设AB边上的高为h，因为△AOB的面积是12，AB＝3，易得h＝8.又因为△AOB与△DOC成中心对称，△COD≌△AOB，所以△DOC中CD边上的高是8.
1.判断正误： （1）轴对称的两个图形一定是全等形，但全等的两个图形不一定是轴对称的图形.（ ） （2）成中心对称的两个图形一定是全等形.但全等的两个图形不一定是成中心对称的图形. （ ） （3）全等的两个图形，不是成中心对称的图形，就是成轴对称的图形. （ ）
2. 如图，△ABC与△A1B1C1关于点O成中心对称，下 列说法：①∠BAC=∠B1A1C1；②AC=A1C1； ③OA=OA1；④△ABC与△A1B1C1的面积相等.其中正确的有（ ）  A.1个 B．2个 C．3个 D．4个
3.如图，已知等边三角形ABC和点O，画△A′B′C′,使△A′B′C′和△ABC关于点O成中心对称.
对应点的连线经过对称中心，且被对称中心平分
应用1：作中心对称图形；应用2：找出对称中心.