









- 第1章+1.1.2集合的概念基础班课件+教案 课件 63 次下载
- 第1章+1.2集合间的基本关系基础班课件+教案 课件 62 次下载
- 第1章+1.3集合的基本运算第一课时基础班课件+教案 课件 68 次下载
- 第1章+1.3集合的基本运算第二课时基础班课件+教案 课件 61 次下载
- 第1章+1.4充分条件与必要条件第一课时基础班课件+教案 课件 56 次下载
高中数学人教A版 (2019)必修 第一册1.1 集合的概念评课ppt课件
展开第一章 集合与常用逻辑用语
高中数学/人教A版/必修一
1.1.1 集合的含义
看下面的例子:(1)1~11之间的所有偶数;(2)方程 x2-2x-3=0 的所有实数根;(3)所有的正方形;(4)到直线l的距离等于定长d的所有的点;(5)立德中学今年入学的全体高一学生.
一般地,我们把研究对象统称为元素; 把一些元素组成的总体叫做集合(简称为集)
以上例子中,我们研究的对象分别是什么?
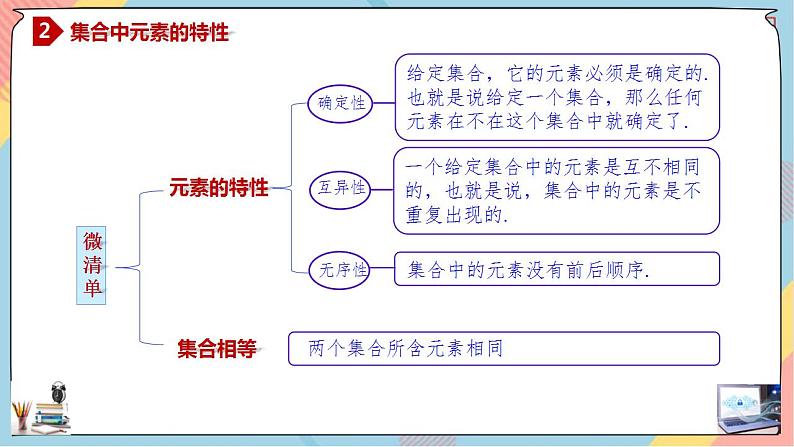
1)确定性 给定的集合,它的元素必须是确定的. 也就是说,给定一个集合,那么一个元素 在或不在这个集合中就确定了.
“我们班的所有高个子男同学构成一个集合”这个说法对吗? 为什么?
“我们班的所有男同学构成一个集合”这个说法对吗?为什么?
不对! 不满足确定性
2)互异性 一个给定集合中的元素是互不相同的. 也就是说,集合中的元素是不重复出现的.
下图中不同信号灯颜色组成的集合中,元素的个数是多少? 为什么?
3个 重复的只能算作一个
3)无序性 同一个集合中的元素列举时无需讲究先后顺序.
特别地,只要构成两个集合的元素相同,就称这两个 集合相等,与元素出现顺序无关.
2)单词“eat”所含字母构成的集合与单词“tea”所含字母 构成的集合是否相等?为什么?
1)电话号码“120”所含字符构成的集合与号码“122”所含 字符构成的集合是否相等?为什么?
不相等!元素不完全相同
相等!元素完全相同
两个集合所含元素相同
给定集合,它的元素必须是确定的.也就是说给定一个集合,那么任何元素在不在这个集合中就确定了.
一个给定集合中的元素是互不相同的,也就是说,集合中的元素是不重复出现的.
1.判断以下元素的全体是否组成集合,并说明理由. (1)大于0且小于10的奇数; (2) 我国境内的高山.
(1)是,确定由1,3,5,7,9五个元素组成的集合.
(1)错误!不满足集合元素的互异性.
(2)错误!依据元素的无序性,这两个集合相等.
(2)否,“高山”不具有确定性.
我们通常用大写拉丁字母A、B、C…表示集合;用小写拉丁字母a、b、c、…表示集合中的元素.
元素、集合的表示及关系
如果a是集合A中的元素,就说a属于A. 记作a∈A
如果a不是集合A中的元素,就说a不属于A. 记作a ∉A
用符号“∈”或“ ∉”填空:
1)若所有奇数组成集合A,则 2 A, 3 A; 2)若所有小于4的实数组成集合B,则 B, B.
数学中一些常用的数集及其记法
0 N; -3 N; 0.5 Z; Z; Q; π R .
提醒:0∈N, 但 0 ∉N*.
1.判断下列每组对象能否构成集合?为什么?
是否构成集合问题常用解决策略: 1)正面判断:研究的对象是不是确定的; 2)反面排除:只要有形容词描述的对象,就不具备确定性.
(1)校园内的大树; (2)所有的三角形;(3)方程x2-9=0在实数范围内的解;(4)高中数学必修一课本中所有的难题.
(1)不能 “大树”不具有确定性;(2) 能 三角形具有确定性;(3)能 该方程实数解确定; (4) 不能 “难题”不具有确定性;
核心素养 之 数学抽象
元素个数问题常用策略: 1)直接列举;(本题列举过程中用到了数值迭代) 2)通过转化与化归,得到元素的范围后再计数; 3)通过递推等手段,使条件显性化,再确定元素.
2. 设A是一些实数组成的集合,满足条件: 若a∈A,则 ∈A,且2 ∉A. (1) 若1∈A,则A中元素个数为 .
4 2-a
1∈A 4∈A -2∈A 1∈A
核心素养 之 数据分析 + 逻辑递推
这里将元素个数问题转化为方程是否有解的问题. 用到了方程思想.
不能! 因为方程a= 无实数解.
2. 设A是一些实数组成的集合,满足条件: 若a∈A,则 ∈A,且 2 ∉A. (2) A能否只包含一个元素?为什么?
这里元素个数问题的解决分两步:先确定元素范围,再对照条件列举验证.用到了重要的策略:有序思考.
先定量判断:-4≤2-a≤4 且 a≥0 再有序列举: a=0时,符合; a=1时,符合; a=2时,无意义; a=3时,符合; a=4时,符合; a=5时,不符合; a=6时,符合.
变题 设A是一些实数组成的集合,若a∈A,则 a∈N , 且 ∈Z. 则A中元素最多有 个.
当a=0,或a=1,或a=a2时,A只有两个元素0和1,不符! 当a2=0时,a=0,不符! 当a2=1时,a=1或-1 若a=1,不符! 若a=-1,则A中有三个元素0,1,-1,符合条件. 综上所述,得a=-1 .
元素含字母问题常用解决策略: 1)有序思考:不重复,不遗漏; 2)分层讨论:先按大类讨论,若需要某一类内部可再讨论; 3)检验互异性:对照已知条件判断合理与否.
1. 已知0∈A,1∈A,a∈A, a2∈A,且A是包含三个 元素的集合,求实数a的值.
数学思想 之 分类讨论
U是以A为圆心、3为半径的圆内(含边界)的点的 集合(点集). 由已知及图形分析得:AB= 4 > 3 , AE=2.5<3, 故B U、Q U.
点集问题解决策略:1)将条件中的符号语言翻译成文字语言和图形语言; 2)结合图形,确定点集对应的区域;3)点与点集的关系,取决于点在区域内或外.
2.如图,长方形ABCD中,AB=4, AD=3; 已知U是长方形ABCD所在 平面内所有满足AM≤3的点M组成的集合. 已知E是AC中点,则 B U,E U.(填“∈”或“ ∉”)
数学思想 之 数形结合
求参数范围问题常用解决策略: 将条件中的符号语言准确翻译成参数应满足的条件.
先将符号语言翻译成文字语言: “2∈A” 表示x=2时x
一、本节课学习的新知识:
二、本节课提升的核心素养:
逻辑推理(有序思考 分类讨论 反证法)
三、本节课训练的数学思想方法:
基础作业: .
能力作业: .
高中数学苏教版 (2019)必修 第一册1.1 集合的概念与表示图文ppt课件: 这是一份高中数学苏教版 (2019)必修 第一册1.1 集合的概念与表示图文ppt课件,共60页。PPT课件主要包含了必备知识·自主学习,元素与集合的关系,a∈A,a∉A,N或N+,关键能力·合作学习,课堂检测·素养达标,一一列举,有限个,无限个等内容,欢迎下载使用。
高中数学人教B版 (2019)必修 第一册1.1.1 集合及其表示方法教课ppt课件: 这是一份高中数学人教B版 (2019)必修 第一册1.1.1 集合及其表示方法教课ppt课件,共30页。PPT课件主要包含了学习目标,探究点一集合的概念等内容,欢迎下载使用。
人教A版 (2019)必修 第一册1.1 集合的概念集体备课ppt课件: 这是一份人教A版 (2019)必修 第一册1.1 集合的概念集体备课ppt课件,文件包含新人教A版数学必修第一册第1章+11集合的概念基础班第二课时课件pptx、新人教A版数学必修第一册第1章+11集合的概念基础班第二课时教案docx等2份课件配套教学资源,其中PPT共22页, 欢迎下载使用。













