北师大版七年级下册1 两条直线的位置关系教学设计

课时安排： 2 课时

课型：新授课

第 1 课时

教

学

目

标

知识与技能

1、在具体的现实情境中，了解同一平面内两条直线的位置关系是平行和相交，理解对顶角、余角、补角等概念。

2、探索并掌握对顶角相等、同角或等角的余角相等、同角或等角的补角相等的性质。

技能目标

经历观察、操作、推理、交流等过程，进一步发展空间观念，推理能力和有条理表达的能力。

情感目标

学会在具体情境中从数学的角度发现和提出问题；敢于发表自己的想法，培养合作交流的意识．

重点

余角、补角、对顶角的性质及其应用。

难点

通过简单的推理，归纳出余角、补角的性质，并能用规范的语言描述性质。

问题与情境

师生行为

设计意图

活动1：

创设情境，引入新课

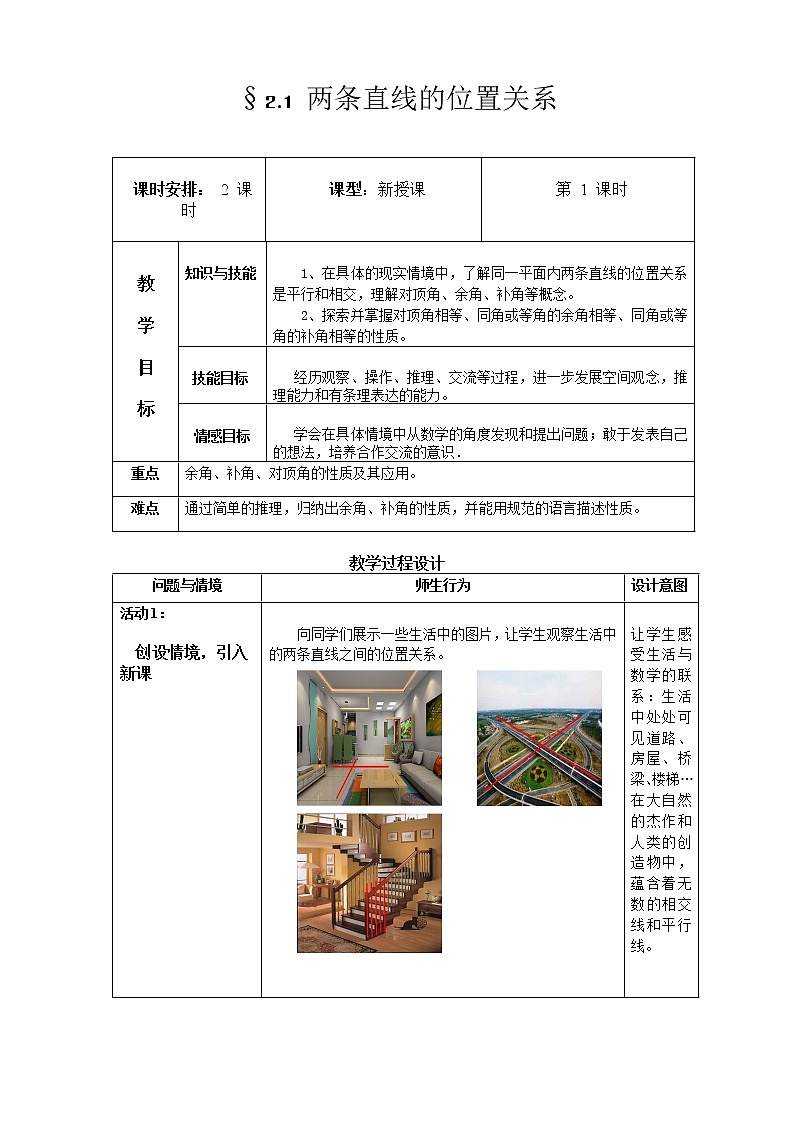
向同学们展示一些生活中的图片，让学生观察生活中的两条直线之间的位置关系。

让学生感受生活与数学的联系：生活中处处可见道路、房屋、桥梁、楼梯…在大自然的杰作和人类的创造物中，蕴含着无数的相交线和平行线。

活动2：

1.互动探究一、平行线、相交线的概念；

1. 问题1 ：

在生活中，你常见的同一平面内的两直线有哪些位置关系？你能给它们下定义吗？

提问1：哪位同学说一说相交线、平行线有什么特点？

生：相交线有一个公共点，平行线没有公共点．

提问2：你能给出相交线和平行线的定义吗?

生：……

提问3：“没有公共点的的两条直线就是平行线”对不对呢？

提示一下，我们教室里面就有，它们没有公共点，但是也是不平行的。

提问4：刚才同学们发现的两条线，不平行也没有交点，你发现为什么了吗？       （学生思考交流）

生：这两条线位于两个平面内。

提问5：那么相交线、平行线该怎么定义呢？

生：在同一平面内，若两条直线只有一个公共点，称这两条直线为相交线．在同一平面内，不相交的两条直线叫做平行线．

（教师板书强调关键词：同一平面、只有一个公共点、不相交）

本环节的任务：从学生身边熟悉的图形出发，让学生在直观有趣的问题情境中学到有价值的数学；

在相互探讨中激发学生学习的积极性，亲身经历提炼有关数学信息的过程，总结出同一平面内两条直线的基本位置关系，提高课堂效率．

2.探究二、对顶角的概念和性质：

提问1：图中∠1与∠2的位置有什么关系？

生：∠1与∠2对称．

生：∠1与∠2有公共的顶点．[来源:学*科*网]

生：∠1与∠2的两边互为反向延长线．

师：你们观察的很认真．像∠1与∠2有公共顶点，两边互为反向延长线，具有这种位置关系的两个角叫做对顶角．

（教师板书并强调关键词：公共顶点、两边互为反向延长线）

提问2 ：∠1与∠2的大小有什么关系？为什么？

生：∠1与∠2相等．

提问3 ：你们能想办法验证一下吗？

（学生开始动手操作，有的同学开始用量角器测量，有的开始动手折叠．完成后让学生先在小组内交流，然后再在全班展示）

提问4 ：数学需要严谨的推理证明，那你能用数学推理的方法证明这两个角相等吗？

由此我们可以得出对顶角的性质：对顶角相等．

例1 下列各图中，∠1与∠2是对顶角的是（    ）

方法总结：对顶角是由两条相交直线构成的，

只有两条直线相交时，才能构成对顶角．

让学生通过观察、操作、推理、交流等活动，使学生在自主学习的过程中，学会对顶角的概念及性质．同时利用学习过的有关事实解决问题，进一步巩固了对顶角的概念及其性质．

3.探究三、余角、补角的概念和性质：

提问1：在刚才我们所画的图形中，∠1与∠3有什么数量关系？

生：∠1与∠3的和是180°．[来源:学科网]

概念：如果两个角的和是180°，那么称这两个角互为补角．

其中一角是另一个角的补角。即：∠1的补角是∠3；∠3的补角是∠1。那么在图形中还有哪些角是互为补角的？

问题：

（1）定义中的“互为”一词如何理解？

（2）∠1 + ∠2 + ∠3 = 180°，能说∠1 、∠2、 ∠3 互补吗？

（3）互补的两角是否一定有公共顶点或公共边？

请同学们注意，互补是指两个角之间的数量关系，与它们的位置无关。

类似地，如果两个角的和是900，那么称这两个角互为余角．比如:直角三角形中的两个锐角互余。

（以类比的方式让学生自己给出互余的定义）

展示（1）：和为90°的两个角．

展示（2）：和为1800的两个角．[来源:Z&xx&k.Com]

在相互补充、相互学习中，体验“互补互余”仅仅表明了两个角的度量关系，并没有限制角的位置关系；让学生在合作共赢中，更好地掌握新知识．同时掌握类比思想。

4. 探究四：补角和余角的性质

新闻：

我国17岁台球新秀丁俊晖在前段时间举行的台球大师比赛中进入了16强。这次比赛中，这位中国少年                                  再次创新记录，成为在这项已有29年历史的赛事中最年轻的参赛者，也改写了中国在亚运会台球项目中没有金牌的历史。

如图1，打台球时，选择适当的方向用白球击打红球，反弹后的红球会直接入袋，此时∠1=∠2，将图1简化成图2，ON与DC交于点O，∠DON=∠CON=900，∠1=∠2.

小组合作交流，解决下列问题：在图2中

问题1：哪些角互为余角？哪些角互为补角？

问题2：∠3与∠4有什么关系？为什么？

问题3：∠AOC与∠BOD有什么关系？为什么？

得出余角各补角的性质：同角或者等角的余角相等．同角或者等角的补角相等．

以学生感兴趣的体育新闻为情景，为学生提供了观察、操作、推理、等数学活动，使学生在自主学习的过程中，掌握“同角或者等角的补角相等．”“同角或者等角的余角相等．”并能够用自己的语言说出简单推理．

活动3

练习巩固，培养能力

例1．已知：如图，直线AB与CD交于点O，∠EOD=90°，回答下列问题：

（1）∠AOE的余角是           ；补角是             ．

（2）∠AOC的余角是       ；补角是        ；对顶角是        ．

巩固本节课的知识点，检验学生的掌握程度．要及时反馈，关注学生易错点，及时进行强调巩固．

例2.（1） 42°角的余角是           ；

     （2） 56°角的余角的补角是           ； 

     （3）若一个角的补角等于它的余角的4 倍，求这个角的度数.

活动4  

课堂练习

活动5

课堂小结，

知识归纳

   练习1、如图，直线AB、CD，EF相交于点O，∠1＝40°，∠BOC＝110°，求∠2的度数.

练习2．如图，点O在直线AB上，OC平分∠BOD，OE平分∠AOD，请找出∠COD的余角和补角，并说明理由．

    完成了本节课的学习，请学生清点收获。由教师开出清单，学生进行以下清点：

1.你学到了哪些知识？

2.你学会了哪些方法？

3.你认为应注意哪些问题？

4.你还有哪些困惑？

作业：教科书习题2.1 第1、2、3、4题

板书设计：

2.1 两条直线的位置关系（1）

1．两条直线的位置关系：相交和平行．[来源:Z§xx§k.Com]

2．对顶角：

性质：

3．补角、余角定义：

4．性质：

同角或者等角的余角相等

同角或者等角的补角相等[来源:Zxxk.Com]

板演区