2020-2021学年3 垂径定理示范课ppt课件

这是一份2020-2021学年3 垂径定理示范课ppt课件，共14页。PPT课件主要包含了学习目标，垂径定理的探究，垂径定理，想一想，垂径定理的推论，随堂练习，课堂小结等内容，欢迎下载使用。
1、探索并证明垂径定理.（重点）2、探索垂径定理的推论.（重点）3、能够用垂径定理及其推论进行简单计算.（难点）
如图:AB是圆O的一条弦,作直径CD,使CD⊥AB,垂足为M. （1）该图是轴对称图形吗？如果是,其对称轴是什么？ （2）图中有哪些等量关系？说一说你的理由.
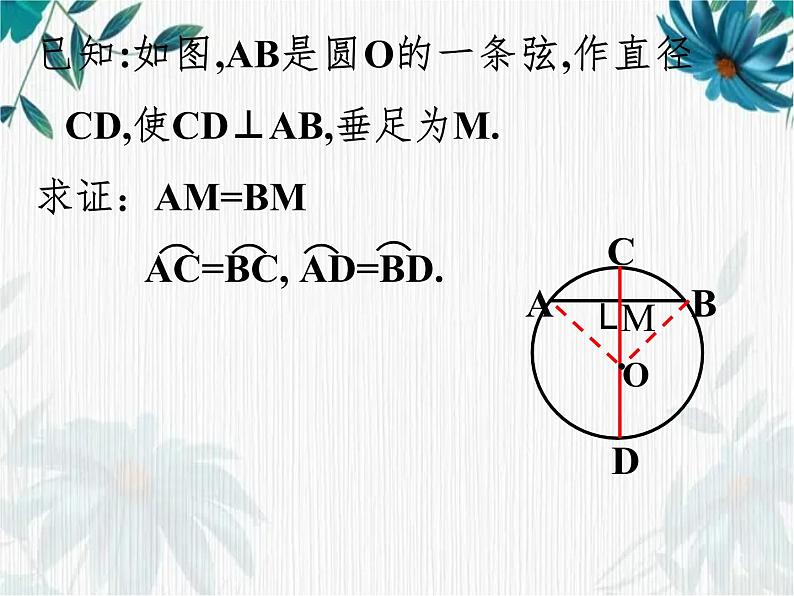
已知:如图,AB是圆O的一条弦,作直径 CD,使CD⊥AB,垂足为M.求证：AM=BM AC=BC, AD=BD.
∵ CD是直径 ,
垂直于弦的直径平分这条弦, 并且平分弦所对的两条弧.
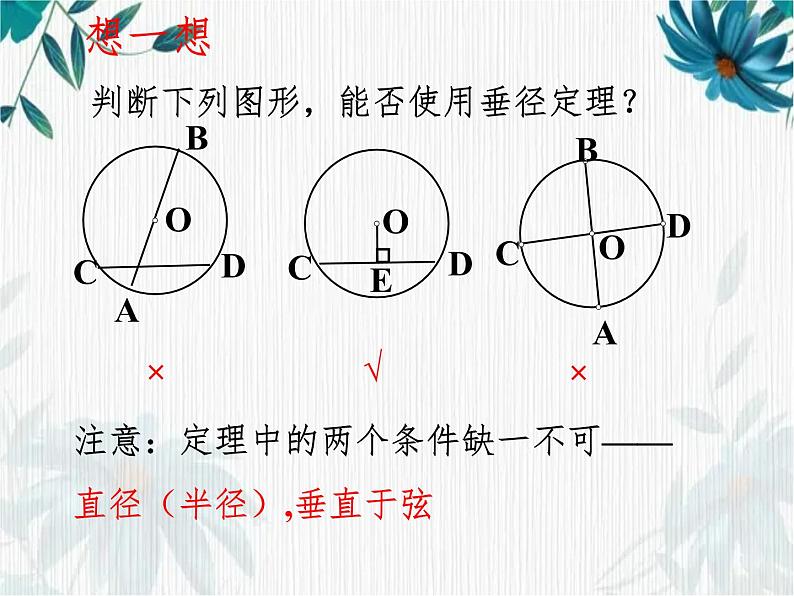
判断下列图形，能否使用垂径定理？
注意：定理中的两个条件缺一不可——直径（半径）,垂直于弦
二、垂径定理推论的探究
① CD是直径
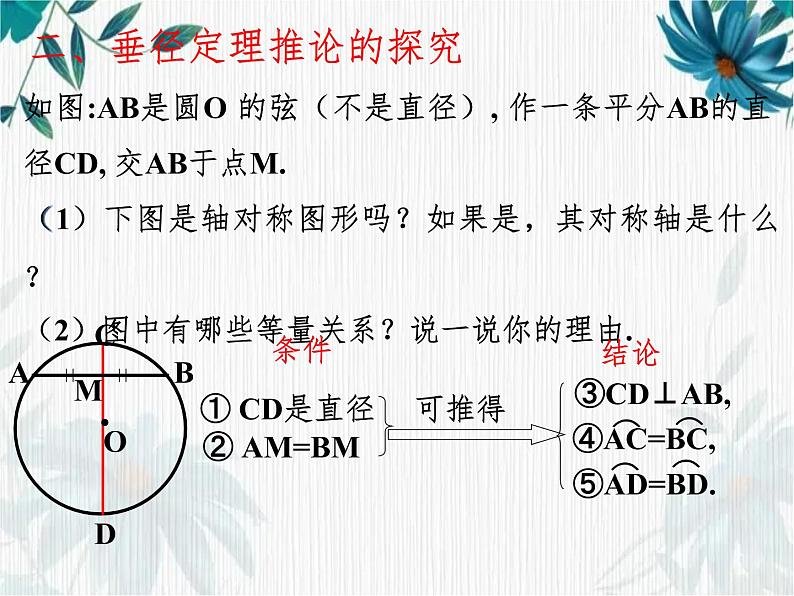
如图:AB是圆O 的弦（不是直径）, 作一条平分AB的直径CD, 交AB于点M.（1）下图是轴对称图形吗？如果是，其对称轴是什么？ （2）图中有哪些等量关系？说一说你的理由.
平分弦（不是直径）的直径，垂直于弦,并且平分弦所对的两条弧.
思考：“不是直径”这个条件能去掉吗？如果不能，请举出反例.
圆的两条直径是互相平分的
1、如图: 若圆O的半径10cm且OE⊥AB于E, OE=6cm, 则AB= cm.
三、垂径定理及其推论的简单应用
2、如图:圆O的直径CD垂直弦AB于点E,且CE=2,DE=8,则AB的长为（ ）A. 2 B. 4 C. 6 D. 8
四、垂径定理的及其推论实际应用
1400年前,我国隋朝建造的赵州石拱桥的桥拱是圆弧形,它的跨度（弧所对的弦长）为37.4米,拱高（即弧的中点到弦的距离）为7.2米,求桥拱所在圆的半径,（结果精确到0.1米）.
谈谈本节课有哪些收获和体会？