初中数学人教 版八年级下册 测试教案

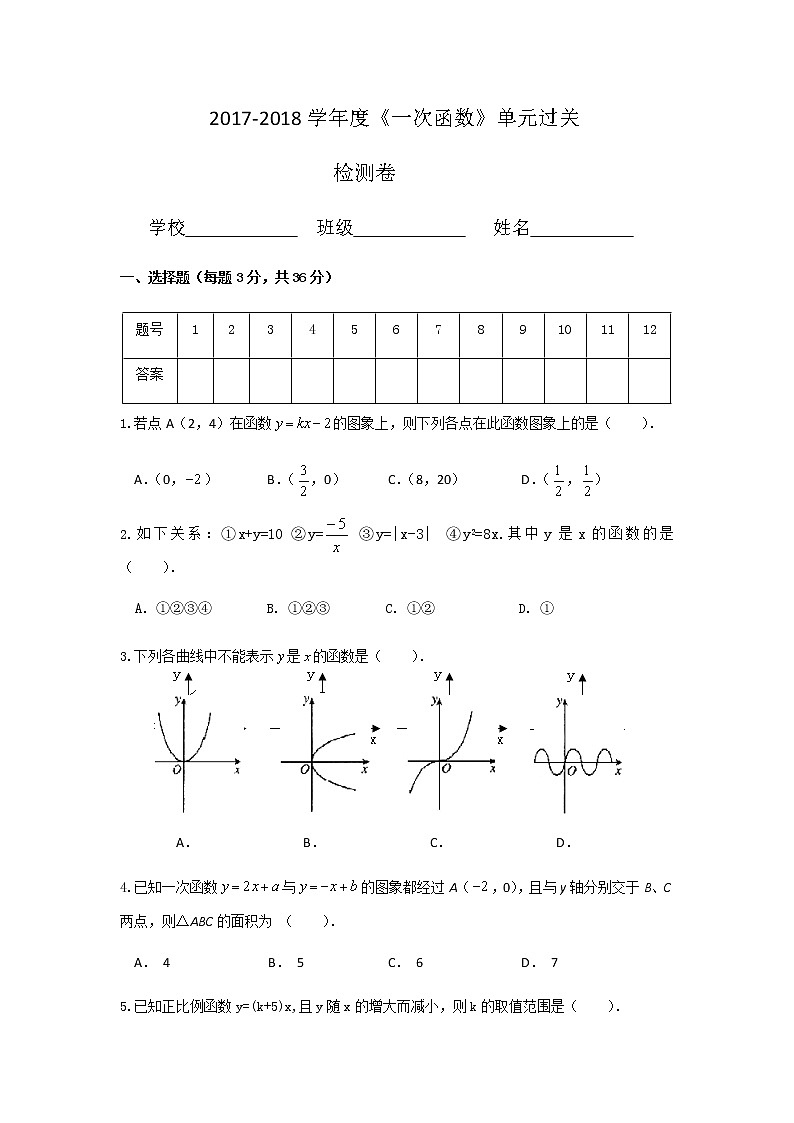
2017-2018学年度《一次函数》单元过关

检测卷

   学校              班级               姓名          

一、选择题（每题3分，共36分）

1.若点A（2，4）在函数的图象上，则下列各点在此函数图象上的是（    ）．

A．（0，）       B．（，0）      C．（8，20）        D．（，）

2.如下关系：①x+y=10 ②y= ③y=|x-3|  ④y2=8x.其中y是x的函数的是（    ）．

A. ①②③④       B. ①②③        C. ①②            D. ①

3.下列各曲线中不能表示是的函数是（    ）．

A．               B．               C．               D．

4.已知一次函数与的图象都经过A（，0），且与y轴分别交于B、C两点，则△ABC的面积为 （    ）．

A． 4              B． 5            C． 6              D． 7

5.已知正比例函数y=(k+5)x,且y随x的增大而减小，则k的取值范围是（    ）．

A.k＞5           B.k＜5      C.k＞-5       D.k＜-5

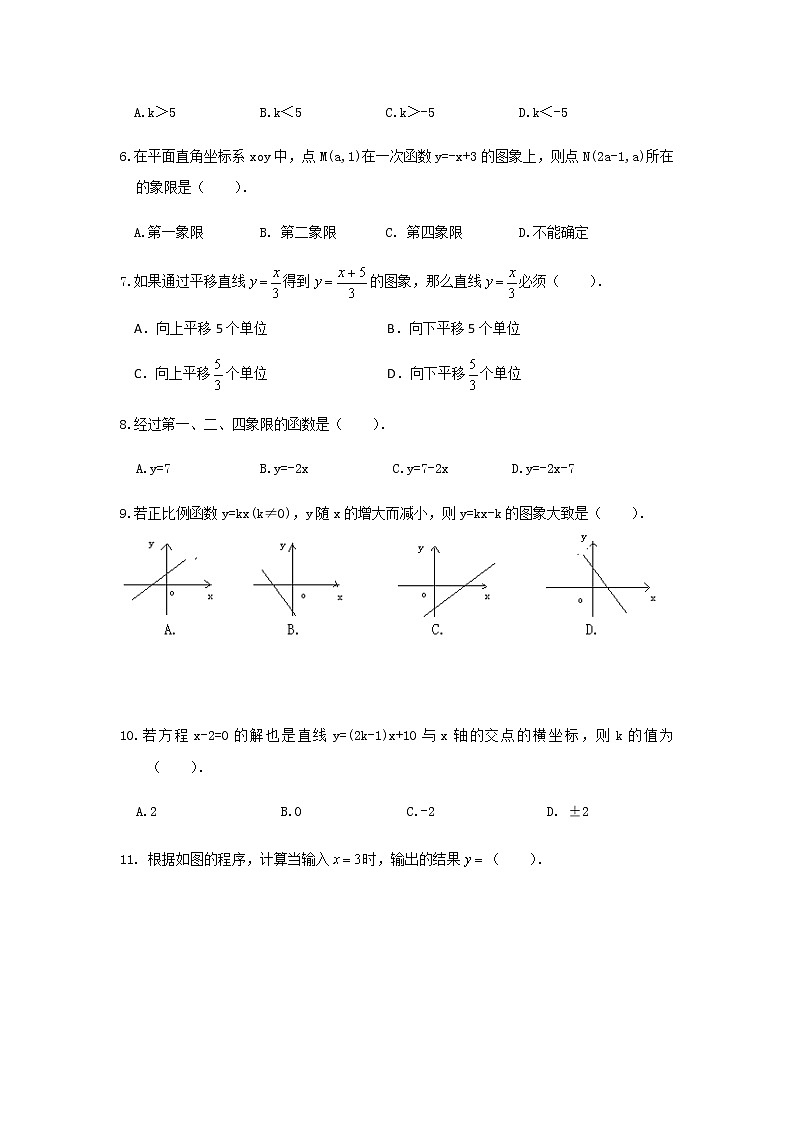
6.在平面直角坐标系xoy中，点M(a,1)在一次函数y=-x+3的图象上，则点N(2a-1,a)所在的象限是（    ）．

  A.第一象限      B. 第二象限       C. 第四象限      D.不能确定

7.如果通过平移直线得到的图象，那么直线必须（    ）．

  A．向上平移5个单位                 B．向下平移5个单位

C．向上平移个单位                 D．向下平移个单位

8.经过第一、二、四象限的函数是（    ）．

A.y=7          B.y=-2x         C.y=7-2x      D.y=-2x-7

9.若正比例函数y=kx(k≠0)，y随x的增大而减小，则y=kx-k的图象大致是（    ）．

10.若方程x-2=0的解也是直线y=(2k-1)x+10与x轴的交点的横坐标，则k的值为（    ）．

A.2          B.0         C.-2        D. ±2

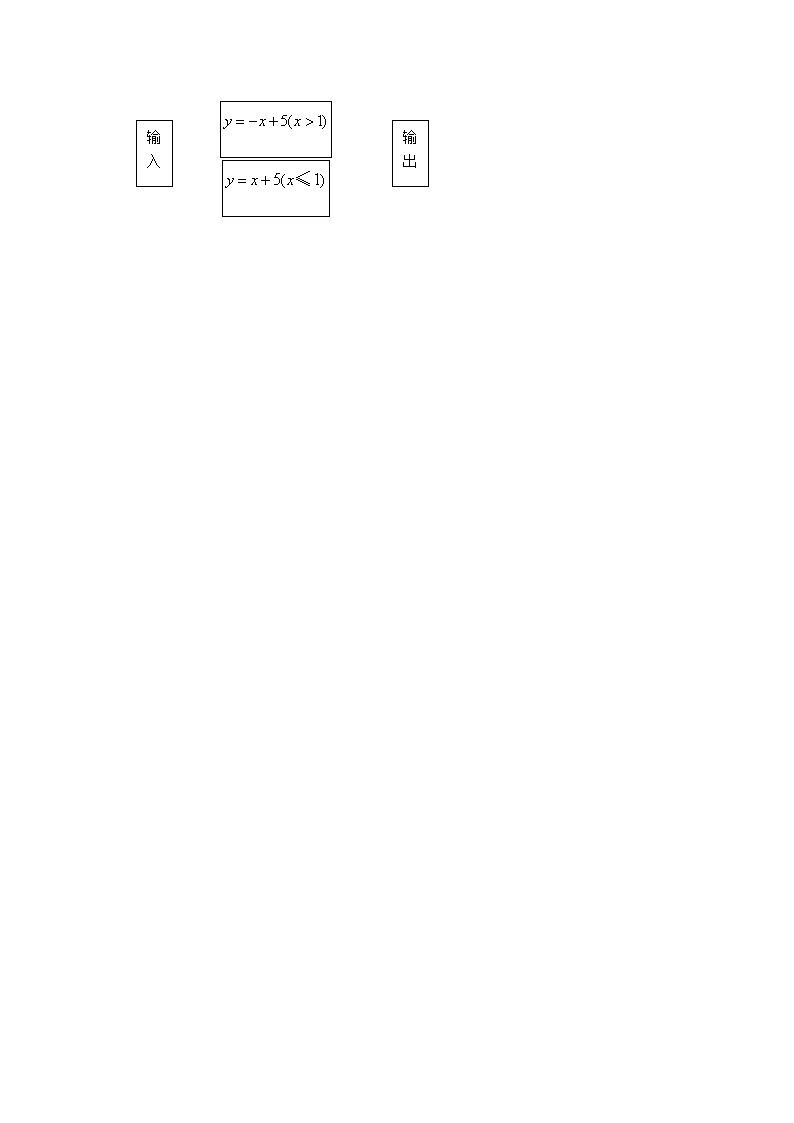
11. 根据如图的程序，计算当输入时，输出的结果（    ）．

A.8          B.-8         C.2        D. -2

12.“龟兔赛跑”讲述了这样的故事：领先的兔子看着缓慢爬行的乌龟，骄傲起来，睡了一觉，当它醒来时，发现乌龟快到终点了，于是急忙追赶，但为时已晚，乌龟先到了终点。用S1、S2分别表示乌龟和兔子所行的路程，t为时间，则下列图象中与故事相吻合的是（    ）

A．               B．               C．                 D．

二、填空题（每小题3分，共18分）

13.已知是关于x的一次函数，则m         ，n         ．

14．直线与x轴的交点坐标是__________，与y轴的交点坐标是__________．

15．当直线与直线平行时，k__________，b___________．

16．汽车行驶前，油箱中有油55升，已知每百千米汽车耗油10升，油箱中的余油量Q（升）与它行驶的距离s（百千米）之间的函数关系式为__________________________；为了保证行车安全，油箱中至少存油5升，则汽车最多可行驶____________千米．

17.某市自来水公司为了鼓励市民节约用水，采取分段收费标准，某市居民每月交水费y（元）与水量x（吨）的函数关系如图所示，请你通过观察函数图象，回答自来水公司收费标准：若用水不超过5吨，水费为________元/吨；若用水超过5吨，超过部分的水费为__________元/吨。

18.已知直线y1=2x与直线y2= -2x+4相交于点A.有以下结论：①点A的坐标为A(1,2);②当x=1时，两个函数值相等；③当x＜1时，y1＜y2④直线y1=2x与直线y2=-2x+4在平面直角坐标系中的位置关系是平行.其中正确的是___________________.

三、解答题（本大题共5个小题，共46分。解答应写出文字说明、证明过程或演算步骤）。

19.（8分）根据下列条件分别确定函数的解析式：

（1）y与x成正比例，当x=2时，y=3;

（2）直线y=kx+b经过点（2,4）与点（.

20.（8分）右图是某汽车行驶的路程s(km)与时间t(分钟) 的函数关系图。

观察图中所提供的信息，解答下列问题：

（1）汽车在前9分钟内的平均速度是         ；

（2）汽车在中途停了多长时间？             ；

（3）当16≤t ≤30时，求S与t的函数关系式。

21．（10分）如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y（元）与通话时间t（分钟）之间的函数关系的图象．

（1）写出y与t之间的函数关系式；

（2）通话2分钟应付通话费多少元？通话7分钟呢？

22．（10分）如图正比例函数y=2x的图像与一次函数 y=kx+b的图象交于点A（m,2）,一次函数的图像经过点B（-2，-1）与y轴交点为C与x轴交点为D.

（1）求一次函数的解析式；

（2）求C点的坐标；

（3）求△AOD的面积。

23．（10分）市和市分别有库存的某联合收割机12台和6台，现决定开往市10台和市8台，已知从市开往市、市的油料费分别为每台400元和800元，从市开往市和市的油料费分别为每台300元和500元．

（1）设市运往市的联合收割机为台，求运费关于的函数关系式．

（2）若总运费不超过9000元，问有几种调运方案？

（3）求出总运费最低的调运方案，并求出最低运费．