沪科版七年级下册8.3 完全平方公式与平方差公式教案

这是一份沪科版七年级下册8.3 完全平方公式与平方差公式教案，共4页。
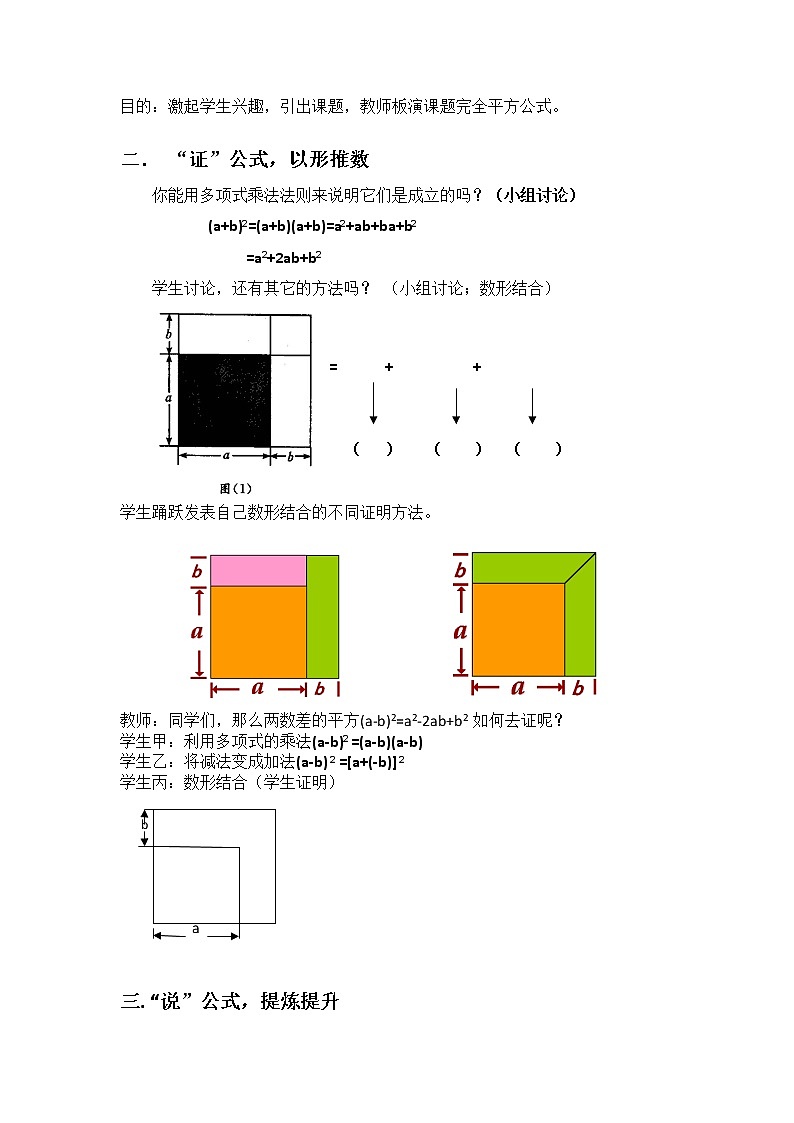
课题：8.3 完全平方公式教学目标：1.完全平方公式的推导及其应用。2.经历探索与证明完全平方公式的过程，发展符号感和推理能力。3.在灵活应用公式的过程中激发学生学习数学的兴趣，培养探索精神。教学重点：完全平方公式的推导过程、结构特点、几何解释，灵活应用。教学难点：理解完全平方公式的结构特征并能灵活应用公式进行计算。教学方法与手段：探究与讲练相结合。教学过程：一．              “引”公式，激情引趣出示图片：七（6）和七（7）班原来都有一个边长为a米的正方形卫生责任区。七（6）班：要求再增加一块边长为b米的正方形卫生区。七（7）班：要求将原卫生区的边长增加b米,扩充为一个边长为（a+b)米的大正方形。另一个学生：咦，你们两个人的要求不是一样的吗？ b                        a                  图（2） (a+b)2=a2+b2？？？古代中国、古埃及、古巴比伦、古印度都曾通过这个图形认识了一个数学公式，你也能从这个图形（图（1））发现这个公式吗？目的：激起学生兴趣，引出课题，教师板演课题完全平方公式。 二．              “证”公式，以形推数你能用多项式乘法法则来说明它们是成立的吗？（小组讨论）       (a+b)2=(a+b)(a+b)=a2+ab+ba+b2                                 =a2+2ab+b2  学生讨论，还有其它的方法吗？ （小组讨论；数形结合） =      +          +          （   ）   （    ）  （    ）  学生踊跃发表自己数形结合的不同证明方法。             教师：同学们，那么两数差的平方(a-b)2=a2-2ab+b2 如何去证呢？学生甲：利用多项式的乘法(a-b)2 =(a-b)(a-b) 学生乙：将减法变成加法(a-b) 2 =[a+(-b)] 2学生丙：数形结合（学生证明）    b                                  a  三. “说”公式，提炼提升       (a+b)2= a2+2ab+b2        (a-b)2=a2-2ab+b2学生观察公式，讨论说出公式的特点：两数和（或差）的平方，等于这两数的平方和，加上（或减去）这两数乘积的两倍。师生一起解读公式的结构特征。记忆口诀：首平方，尾平方，首尾2倍放中央，中间符号同前方。四. “练”公式，学以致用例1   (1) (2m+n)2                  (2) (3x-0.5)2  练习 利用公式计算：（1）(3a+2)2                (3)     (-m+3)2（2）(a-3b)2                (4)     (-x-1)2通过以上例题总结：公式中的字母a,b可以表示数，可以表示单项式，也可以表示多项式。1．纠错练习 指出下列各式中的错误，并加以改正：(1) (2a−1)2＝2a2−2a+1;(2) (2a+1)2＝4a2 +1；2.下面的计算中有些地方用纸牌盖上了，我们来比一比谁能最快地说出纸牌下盖的是什么式子。(1)（3x+2y)2=（）+12xy+4y2(2)(5m-4n)2=25m2-40mn+（） (3)(4a+3b) 2=16a2+（）+9b2 (4)(2x-8y)2=4x2-（）+64y2 例2 速算比赛 (1) 1032                  (2)982 3.生活在线 如图，一块方巾铺在正方形的茶几上，四周刚好都垂下15cm.如果设方巾的边长为a,怎样求茶几的面积？五. “拓”公式，挑战自我小兵计算一个二项整式的平方式时,得到正确结果是4x2+ (    ) +25y2,但中间一项不慎被污染了,这一项应是(     )A 10xy    B 20xy     C±10xy   D±20xy课堂小结：     作业布置：1、课本p69练习第一题           2、p71习题第一题                                               教后反思：