人教版九年级上册第二十四章 圆综合与测试教学ppt课件

这是一份人教版九年级上册第二十四章 圆综合与测试教学ppt课件，共9页。PPT课件主要包含了切线的证明，当堂训练二等内容，欢迎下载使用。

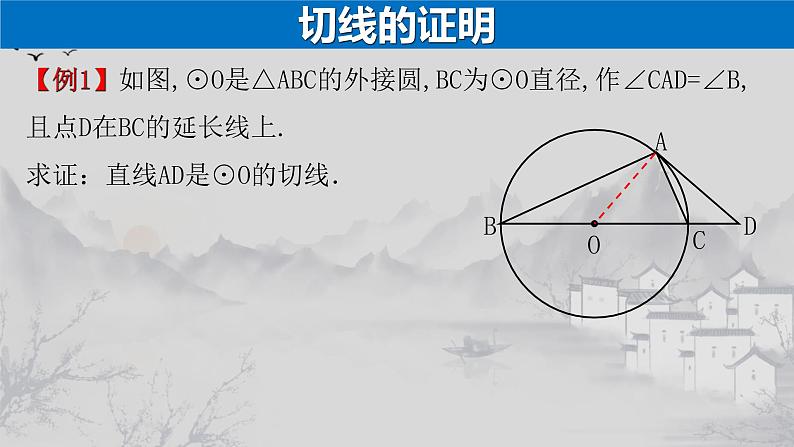
【例1】如图,⊙O是△ABC的外接圆,BC为⊙O直径,作∠CAD=∠B,且点D在BC的延长线上.求证：直线AD是⊙O的切线．
1.如图,AB为⊙O的直径,点P为AB延长线上一点,点C为⊙O上一点，PC=8,PB=4,AB=12.求证：PC是⊙O的切线．
解：连接OC.根据题意，可得OC=6,PO=10,PC=8，∴OC2＋PC2=PO2，∴△POC为直角三角形且∠PCO=90º，∴OC⊥CP，∴PC是⊙O的切线
2.如图,AB是⊙O的弦,OD⊥OB,交AB于E,且AD=ED. 求证：AD是⊙O的切线．
解：连接OA.∵OA=OB,∴∠B=∠OAB. 又∵AD=DE,∴∠DAE=∠DEA， 而∠DEA=∠BEO,∠B＋∠BEO=90º， ∴∠DAE＋∠OAB=90º,∴OA⊥AD， ∴AD是⊙O的切线
3.如图,△ABC内接于⊙O,∠B=60º,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.求证：PA是⊙O的切线．
解：连接OA. ∵∠B=60º,∴∠AOC=120º,∴∠AOP=60º， ∵OA=OC,∴∠OAC=∠ACP=0.5∠AOP=30º，又∵AP=AC,∴∠P=∠ACP=30º， ∴∠PAO=90º,∴OA⊥AP， ∴PA是⊙O的切线
【例2】已知：O为∠BAC平分线上一点,OD⊥AB于D,以O为圆心，OD为半径作⊙O. 求证：⊙O与AC相切.
无交点,作垂直,证半径。
无交点,作垂直,证半径.
2.如图的两个圆是以O为圆心的同心圆,大圆的弦AB是小圆的切线,C为切点. 求证：C是AB的中点.
3.如图,O为正方形对角线上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点M.(1)求证：CD与⊙O相切；(2)若正方形ABCD的边长为1,求⊙O的半径.