浙教版九年级上册第1章 二次函数1.4 二次函数的应用达标测试

     浙教版数学九年级上册

           班级：                姓名：             

一、单选题

1．小兰画了一个函数y=x2+ax+b的图象如图，则关于x的方程x2+ax+b=0的解是（　　） 

A．无解 B．x=1 C．x=﹣4 D．x=﹣1或x=4

【答案】D

【解析】解：如图，∵函数y=x2+ax+b的图象与x轴交点坐标分别是（﹣1，0），（4，0）， 

∴关于x的方程x2+ax+b=0的解是x=﹣1或x=4．

2．二次函数y=ax2+bx+c的图象如图所示，则在下列说法中，与此函数的系数相关的一元二次方程ax2+bx+c=0的根的情况，说法正确的是（　　）

A．方程有两个相等的实数根 B．方程的实数根的积为负数

C．方程有两个正的实数根 D．方程没有实数根

【答案】B

【解析】解：根据图象可以看出抛物线与x轴有两个不同的交点，

故与此函数的系数相关的一元二次方程ax2+bx+c=0有两个不相等的实数根，

由于两交点位于原点的两侧，

故一元二次方程ax2+bx+c=0有一正根一负根，故只有B正确；

3．抛物线 与x轴只有一个交点，则m的值为（　　）  

A．－ 6 B．6 C．3 D．9

【答案】D

【解析】∵二次函数y=x2﹣6x+m的图象与x轴只有一个公共点，∴y=0时，方程x2﹣6x+m=0有两个相等的实数根，∴△=62﹣4×1×m=0．

解得：m=9．

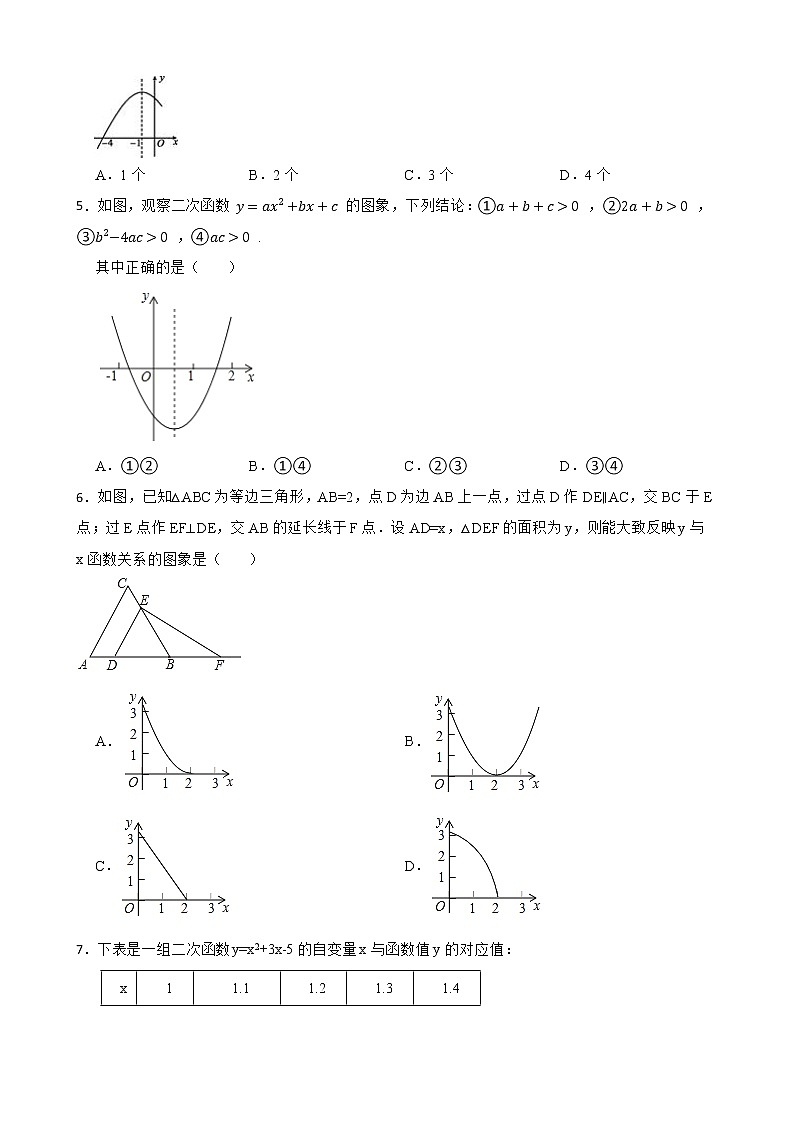
4．二次函数y=ax2+bx+c(a≠0)的部分图象如图4所示,图象过点（-4，0），对称轴为直线x=-1。有下列结论：①abc>0；②2a-b=0；③一元二次方程ax2+bx+c=0的解是x1=-4，x2=1；④当y>0时，-4< x< 2。其中正确的结论有（　　）

A．1个 B．2个 C．3个 D．4个

【答案】C

【解析】解：∵抛物线开口向下，对称轴为直线x=-1，抛物线与y轴的交点在y轴正半轴，
∴a＜0，b＜0，c＞0，
∴abc＞0，
故①正确 ；
∵对称轴为直线x=-1，
∴=-1，
∴2a-b=0，
故②正确；
∵抛物线与x轴的交点为（-4，0）， 对称轴为直线x=-1，
∴抛物线与x轴的另一个交点为（2，0），
∴ 一元二次方程ax2+bx+c=0的解是x1=-4，x2=2，
故③错误；
当-4<x<2时，抛物线在x轴的上方，y＞0，
故④正确，
∴正确的结论有3个.

5．如图，观察二次函数 的图象，下列结论：① ，② ，③ ，④ . 

其中正确的是（　　）

A．①② B．①④ C．②③ D．③④

【答案】C

【解析】由图象可知当x=1时，y＜0，∴ ，故①不正确；

由图象可知 ，∴ ，又∵开口向上，∴a＞0，∴ ，∴ ，故②正确；

由图象可知二次函数与x轴有两个交点，∴方程 有两个不相等的实数根，∴△＞0，即 ，故③正确；

由图象可知抛物线开口向上，与y轴的交点在x轴的下方，∴a＞0，c＜0，∴ ，故④不正确；

综上可知正确的为②③，

6．如图，已知△ABC为等边三角形，AB=2，点D为边AB上一点，过点D作DE∥AC，交BC于E点；过E点作EF⊥DE，交AB的延长线于F点．设AD=x，△DEF的面积为y，则能大致反映y与x函数关系的图象是（　　）
 

A． B．

C． D．

【答案】A

【解析】∵△ABC是等边三角形，

∴∠B=60°，

∵DE∥AB，

∴ ∠EDB=∠ABE=60° ，

∵EF⊥DE，

∴∠DEF=90°，

∴∠F=90°﹣∠EDC=30°；

∵∠ACB=60°，∠EDC=60°，

∴△EDC是等边三角形．

∴ED=DC=2﹣x，

∵∠DEF=90°，∠F=30°，

∴EF=   ED=   （2﹣x）．

∴y=   ED•EF=   （2﹣x）•   （2﹣x），

即y=   （x﹣2）2，（x＜2），

7．下表是一组二次函数y=x2+3x﹣5的自变量x与函数值y的对应值：

那么方程x2+3x﹣5=0的一个近似根是（　　）

A．1 B．1.1 C．1.2 D．1.3

【答案】C

【解析】解：观察表格得：方程x2+3x﹣5=0的一个近似根为1.2，

8．如图，抛物线y=ax2+bx+c与x轴相交于A、B两点，与y轴相交于C点，图中虚线为抛物线的对称轴，则下列正确的是(　　)
 

A．a＜0 B．b＜0 C．c＞0 D．b2-4ac＜0

【答案】B

【解析】由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．

二、填空题

9．抛物线 y=x2+kx+1的最低点在 轴上，则 的值为　        　． 

【答案】±2或-2

【解析】解：∵二次函数y=x2+kx+1的图象的最低点在x轴上，

∴b2-4ac=0，即k2-4=0，

解得k= 2．

10．如图，矩形纸片ABCD中，BC=5，AB=3，点P是BC边上的动点（点P不与点B、C重合）.现将△PCD沿PD翻折，得到△PC′D；作∠BPC′的角平分线，交AB于点E.设BP=x，BE=y，则y与x的函数关系式为　                  　.

【答案】y＝﹣ x2+ x

【解析】解：连接DE，

因为△PCD沿PD翻折，得到△PC′D，故有DP平方 ，

又∵PE平分 ，

∴ ，

已知BP=x，BE=y，BC=5，AB=3，

即在Rt△PCD中， ， ，

即 ，

在Rt△EBP中，BP=x，BE=y，

故 ，

在Rt△ADE中， ， ，

故 ，

在Rt△PDE中， ，

即 ，

化简得：y＝﹣ x2+ x.

11．已知抛物线y=﹣x2﹣2mx+4m+6，当实数m的值为　     　 时，抛物线与x轴的两个交点和它的顶点所组成的三角形面积最小，其最小值是　     　． 

【答案】﹣2；2

【解析】解：y=﹣x2﹣2mx+4m+6=﹣（x+m）2+m2+4m+6，则抛物线的顶点坐标为（﹣m，m2+4m+6）， 

设抛物线与x轴两交点的坐标为（α，0），（β，0），则α、β为方程﹣x2﹣2mx+4m+6=0的两实数解，

所以α+β=﹣2m，αβ=﹣（4m+6），则|α﹣β|= = =2 ，

所以抛物线与x轴的两个交点和它的顶点所组成的三角形面积= •（m2+4m+6）•2 =[（m+2）2+2]• ，

因为m=﹣2时，（m+2）2+2有最小值2， 也有最小值 ，

所以抛物线与x轴的两个交点和它的顶点所组成的三角形面积的最小值为2 ．

12．若抛物线 （ 为常数）的图象与 轴没有交点，则 取值范围为　        　． 

【答案】 ．

【解析】令y=0，则 ，

∵关于x的二次函数 的图像与 轴没有交点，

∴

解得

13．如图所示，抛物线y=ax2+bx+c（a≠0）与x轴的两个交点分别为A（-2，0）和B（6，0），当y＜0时，x的取值范围是　               　．

【答案】 或 ．

【解析】由图可知，当 或 时，

14．如图，记函数y=|-2x2+8x-6|的图象为C1.若直线y=x+m与C1有4个不同的交点，则m的取值范围　           　

【答案】-1＜m＜

【解析】解：令y=0，代入y=-2x2+8x-6，得x1=2，x2=3，

∴图象C1与x轴的交点坐标为：（1，0），（3，0），

当直线y＝x＋m与抛物线y=-2x2+8x-6（1≤x≤3）相切，

直线y＝x＋m与该图象恰有三个不同的交点，

∴2x2-7x+6+m=0有两个相等的根，

∴∆= ,解得：m= ，

当直线y＝x＋m过（1，0）时，直线y＝x＋m与该图象恰有三个不同的交点

此时m=-1，

∴当-1＜m＜ 时，直线y=x+m与C1有4个不同的交点，

15．一养鸡专业户计划用116m长的篱笆围成如图所示的三间长方形鸡舍，门MN宽2m，门PQ和RS的宽都是1m，围成的鸡舍面积最大是　     　平方米.

【答案】450

【解析】解：设鸡舍面积为y平方米，AB＝xm，则AD＝ +1＝（60﹣2x）m

由题意得：y＝x（60﹣2x）＝﹣2x2+60x

∴当x＝﹣ ＝15时，围成的鸡舍面积最大，最大值为：﹣2×152+60×15＝450（平方米）

三、解答题

16．如图，在平面直角坐标系xOy中，边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上，二次函数y=-x2+bx+c的图象经过B、C两点．

（1）求b，c的值．
（2）结合函数的图象探索：当y＞0时x的取值范围．

【答案】（1）∵正方形OABC的边长为2，
∴B（2，2），C（0，2），
把B（2，2），C（0，2）代入y=-x2+bx+c得
，解得；
（2）二次函数解析式为y=-x2+x+2，
当y=0时，-x2+x+2=0，
解得x1=-1，x2=3，
∴抛物线与x轴的交点坐标为（-1，0），（3，0），
∴当-1＜x＜3时，y＞0．

【解析】（1）根据正方形的性质得到B（2，2），C（0，2），然后把B点和C点坐标代入解析式得到关于b、c的方程组，再解方程组即可；
（2）由（1）得到二次函数解析式为y=-x2+x+2，再求出抛物线与x轴的交点坐标，然后根据图象得到当y＞0时x的取值范围．

17．抛物线与x轴的交点为（﹣1，0）、（3，0），且过点（1，4），并直接写出该抛物线关于x轴对称的抛物线的解析式． 

【答案】解：设已知抛物线的解析式为：y=a（x+1）（x﹣3） 

∵该抛物线经过点（1，4），

∴4=（1+1）•（4﹣3）a

∴a=2

即已知抛物线的解析式为：y=2x2﹣4x﹣6

∴该抛物线关于x轴对称的抛物线的解析式：y=﹣2x2+4x+6

【解析】利用两点式求出已知抛物线的解析式．因为关于x轴对称的两个抛物线，自变量x的取值相同，函数值y互为相反数，由此可直接写出所求抛物线的解析式． 

18．进价为每件40元的某商品，售价为每件50元时，每星期可卖出500件，市场调查反映：如果每件的售价每降价1元，每星期可多卖出100件，但售价不能低于每件42元，且每星期至少要销售800件．设每件降价x元 （x为正整数），每星期的利润为y元．

（1）求y与x的函数关系式并写出自变量x的取值范围；

（2）若某星期的利润为5600元，此利润是否是该星期的最大利润？说明理由．

（3）直接写出售价为多少时，每星期的利润不低于5000元？

【答案】解：（1）依题意，得y=（50﹣40﹣x）•（500+100x）=﹣100x2+500x+5000，

∵，

∴3≤x≤8；

（2）y=﹣100x2+500x+5000=﹣100（x﹣）2+5625，

∵x为整数，

∴当x取2或3时，有最大值，为5600，

∴5600是最大利润．

（3）令y=﹣100（x﹣）2+5625≥5000，

解得0≤x≤5时，

即当售价在45到50元时，月利润不低于5000元．

【解析】（1）根据利润y=每件利润×销售量，每件利润=50﹣40﹣x，销售量=500+100x，而售价50﹣x≥42，销售量=500+100x≥800，列不等式组求x的取值范围；

（2）根据（1）的关系式配方后确定 大利润，与5600比较后即可发现是否为最大利润；

（3）设当y=5000时x有两个解，可推出0≤x≤5时，y≥5000．

19．二次函数（a不为0）的图象如图所示，根据图象解答下列问题：

（1）写出方程的两个根．
（2）写出不等式的解集．
（3）写出y随x的增大而减小的自变量的取值范围．
（4）若方程有两个不相等的实数根，求k的取值范围．

【答案】解：（1）∵二次函数y=ax2+bx+c的图象与x轴的交点为（1，0），（3，0）
∴方程ax2+bx+c=0的两个根x1=1，x2=3；
（2）由二次函数y=ax2+bx+c的图象可知：1＜x＜3时，二次函数y=ax2+bx+c的值大于0
∴不等式ax2+bx+c＞0的解集为1＜x＜3；
（3）由图象可知：二次函数y=ax2+bx+c的对称轴为x=2
∴y随x的增大而减小的自变量x的取值范围为x＞2；
（4）由图象可知：二次函数y=ax2+bx+c的顶点坐标为（2，2），
当直线y=k，在（0，2）的下边时，一定与抛物线有两个不同的交点，因而当k＜2时，方程ax2+bx+c=k有两个不相等的实数根．

【解析】（1）看与x轴的交点即可；
（2）看y轴上方的函数图象相对应的x的值即可；
（3）看对称轴右侧的函数图象相对应的x的范围即可；
（4）先移项，整理为一元二次方程，让根的判别式大于0求值即可．