高中数学人教A版 (2019)必修 第一册5.3 诱导公式第2课时学案及答案

这是一份高中数学人教A版 (2019)必修 第一册5.3 诱导公式第2课时学案及答案，共6页。学案主要包含了学习目标，自主学习，经典例题，跟踪训练，当堂达标，课堂小结，参考答案等内容，欢迎下载使用。

【自主学习】
复习回顾：公式一 公式二

公式三 公式四

1.公式五
2.公式六
我们能不能用学过的公式推导出 的正余弦值与α的正余弦值的关系？
【经典例题】
题型一 利用诱导公式证明
例1 (1) (2)
【跟踪训练】

题型二 利用诱导公式化简
例2
【跟踪训练】2 化简

题型三 利用诱导公式求值
例3
【跟踪训练】3
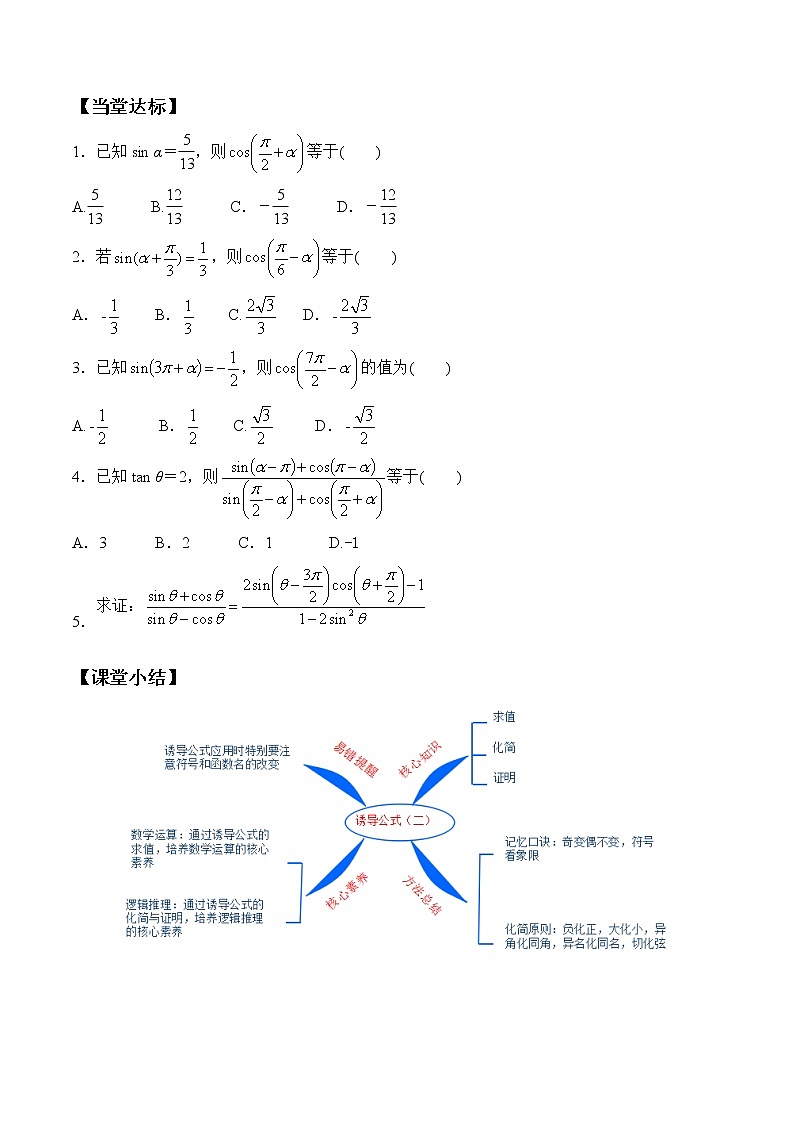
【当堂达标】
1．已知sin α＝eq \f(5,13)，则等于( )
A.eq \f(5,13) B.eq \f(12,13) C．－eq \f(5,13) D．－eq \f(12,13)
2．若，则等于( )
A． B． C. D．
3．已知，则的值为( )
A. B． C. D．
4．已知tan θ＝2，则等于( )
A．3 B．2 C．1 D.-1
求证：
【课堂小结】
【参考答案】
【自主学习】
sin(α+2kπ)=sinα cs(α+2kπ)=csα tan(α+2kπ)=tanα
sin(π+α)=－sinα cs(π+α)=－csα tan(π+α)=tanα
sin(－α)=－sinα cs(－α)=csα tan(－α)=－tanα
sin(π-α)=sinα cs(π-α)=－csα tan(π-α)=－tanα

【经典例题】
例1
【跟踪训练】1
例2
【跟踪训练】2
例3
【跟踪训练】3
【当堂达标】
1.C
2.B
3.A
4.B
所以原等式成立.
5.学习目标
学科素养
1.掌握诱导公式五、六的推导，并能应用于解决简单的求值、化简与证明问题.（重点）
2.对诱导公式一至六，作综合归纳，体会出六组公式的共性与个性，培养由特殊到一般的数学推理意识和能力.（重点）
1、数学运算
2、逻辑推理
sinπ＋α＝
csπ＋α＝
tanπ＋α＝
sin(α+2kπ)= cs(α+2kπ)= tan(α+2kπ)=
sin(π－α)＝
cs(π－α)＝
tan(π－α)＝
sin－α＝
cs－α＝
tan－α＝
sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)－α))＝
cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)－α))＝
sineq \b\lc\(\rc\)(\a\vs4\al\c1(α＋\f(π,2)))＝
cseq \b\lc\(\rc\)(\a\vs4\al\c1(α＋\f(π,2)))＝