
数学必修 第二册9.2 用样本估计总体第一课时教案设计
展开第九章 统计
9.2.1总体取值规律的估计(第一课时)频率分布直方图
一、教学目标
1.结合实例,能用样本估计总体的取值规律.
2.会列频率分布表,画频率分布直方图.
3.能根据频率分布表和频率分布直方图观测数据的分布规律.
4.通过对频率分布直方图的学习,培养学生直观想象、数学运算、数学建模等数学素养。
二、教学重难点
1.列频率分布表,画频率分布直方图;
2.根据频率分布表和频率分布直方图观测数据的分布规律.
三、教学过程:
(1)创设情景
阅读课本,完成下列思考:
①画频率分布直方图的步骤有哪些?
②频率分布直方图的纵轴表示什么?各矩形面积之和等于什么?
(2)新知探究
问题:①列频率分布表的一般步骤是什么?
②能否根据频率分布表来绘制频率直方图?
学生回答教师点拨并(提出本节课所学内容)
(3)新知建构
频率分布直方图绘制步骤:
①求极差,即一组数据中的最大值与最小值的差.
②决定组距与组数.组距与组数的确定没有固定的标准,一般数据的个数越多,所分组数越多.当样本容量不超过100时,常分成5~12组.为方便起见,一般取等长组距,并且组距应力求“取整”.
③将数据分组.
④列频率分布表.计算各小组的频率,第i组的频率是.
⑤画频率分布直方图.其中横轴表示分组,纵轴表示.实际上就是频率分布直方图中各小长方形的高度,它反映了各组样本观测数据的疏密程度.
频率分布直方图意义:各个小长方形的面积表示相应各组的频率,频率分布直方图以面积的形式反映数据落在各个小组的频率的大小,各小长方形的面积的总和等于1.
总体取值规律的估计:我们可以用样本观测数据的频率分布估计总体的取值规律.
频率分布直方图的特征:当频率分布直方图的组数少、组距大时,容易从中看出数据整体的分布特点,但由于无法看出每组内的数据分布情况,损失了较多的原式数据信息;当频率分布直方图的组数多、组距小时,保留了较多的原始数据信息,但由于小长方形较多,有时图形会变得非常不规则 ,不容易从中看出总体数据的分布特点.
(4)数学运用
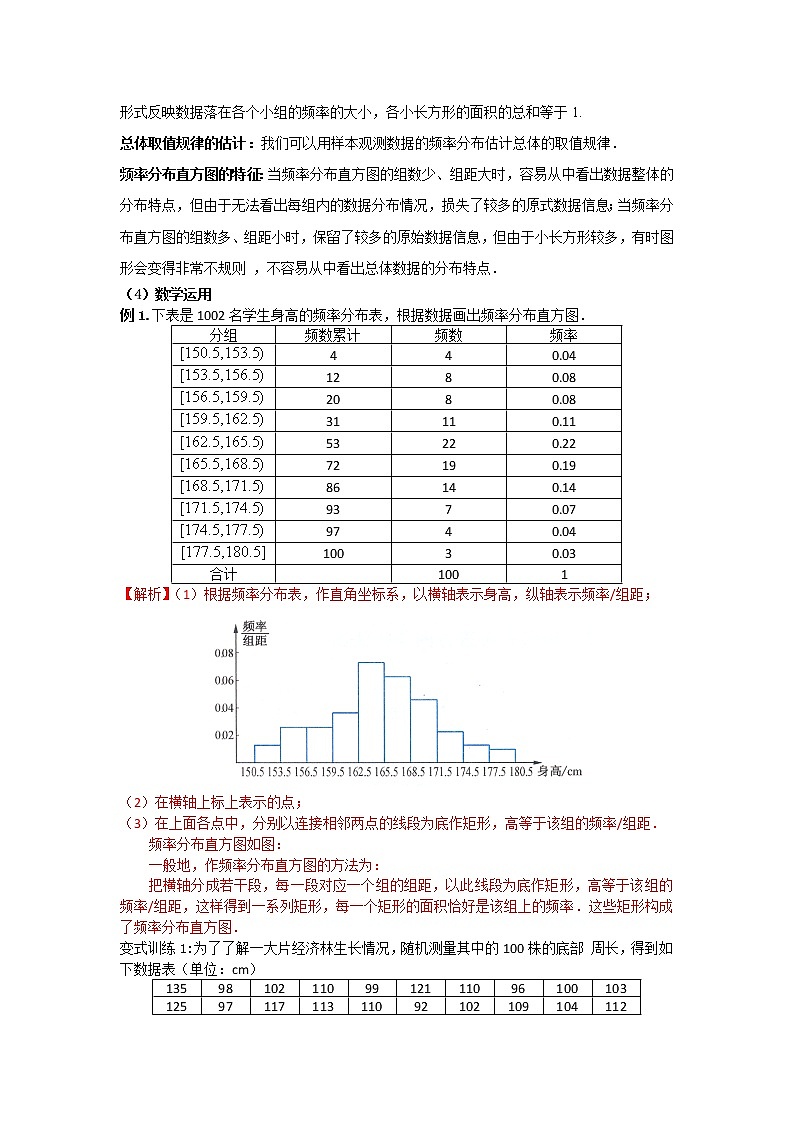
例1.下表是1002名学生身高的频率分布表,根据数据画出频率分布直方图.
分组 | 频数累计 | 频数 | 频率 |
4 | 4 | 0.04 | |
12 | 8 | 0.08 | |
20 | 8 | 0.08 | |
31 | 11 | 0.11 | |
53 | 22 | 0.22 | |
72 | 19 | 0.19 | |
86 | 14 | 0.14 | |
93 | 7 | 0.07 | |
97 | 4 | 0.04 | |
100 | 3 | 0.03 | |
合计 |
| 100 | 1 |
【解析】(1)根据频率分布表,作直角坐标系,以横轴表示身高,纵轴表示频率/组距;
(2)在横轴上标上表示的点;
(3)在上面各点中,分别以连接相邻两点的线段为底作矩形,高等于该组的频率/组距.
频率分布直方图如图:
一般地,作频率分布直方图的方法为:
把横轴分成若干段,每一段对应一个组的组距,以此线段为底作矩形,高等于该组的频率/组距,这样得到一系列矩形,每一个矩形的面积恰好是该组上的频率.这些矩形构成了频率分布直方图.
变式训练1:为了了解一大片经济林生长情况,随机测量其中的100株的底部 周长,得到如下数据表(单位:cm)
135 | 98 | 102 | 110 | 99 | 121 | 110 | 96 | 100 | 103 |
125 | 97 | 117 | 113 | 110 | 92 | 102 | 109 | 104 | 112 |
109 | 124 | 87 | 131 | 97 | 102 | 123 | 104 | 104 | 128 |
105 | 123 | 111 | 103 | 105 | 92 | 114 | 108 | 104 | 102 |
129 | 126 | 97 | 100 | 115 | 111 | 106 | 117 | 104 | 109 |
111 | 89 | 110 | 121 | 80 | 120 | 121 | 104 | 108 | 118 |
129 | 99 | 90 | 99 | 121 | 123 | 107 | 111 | 91 | 100 |
99 | 101 | 116 | 97 | 102 | 108 | 101 | 95 | 107 | 101 |
102 | 108 | 117 | 99 | 118 | 106 | 119 | 97 | 126 | 108 |
123 | 119 | 98 | 121 | 101 | 113 | 102 | 103 | 104 | 108 |
(1)编制频率分布表;(2)绘制频率分布直方图;(3)估计该片经济林中底部周长小于100cm的树木约占多少,周长不小于120cm的树木约占多少.
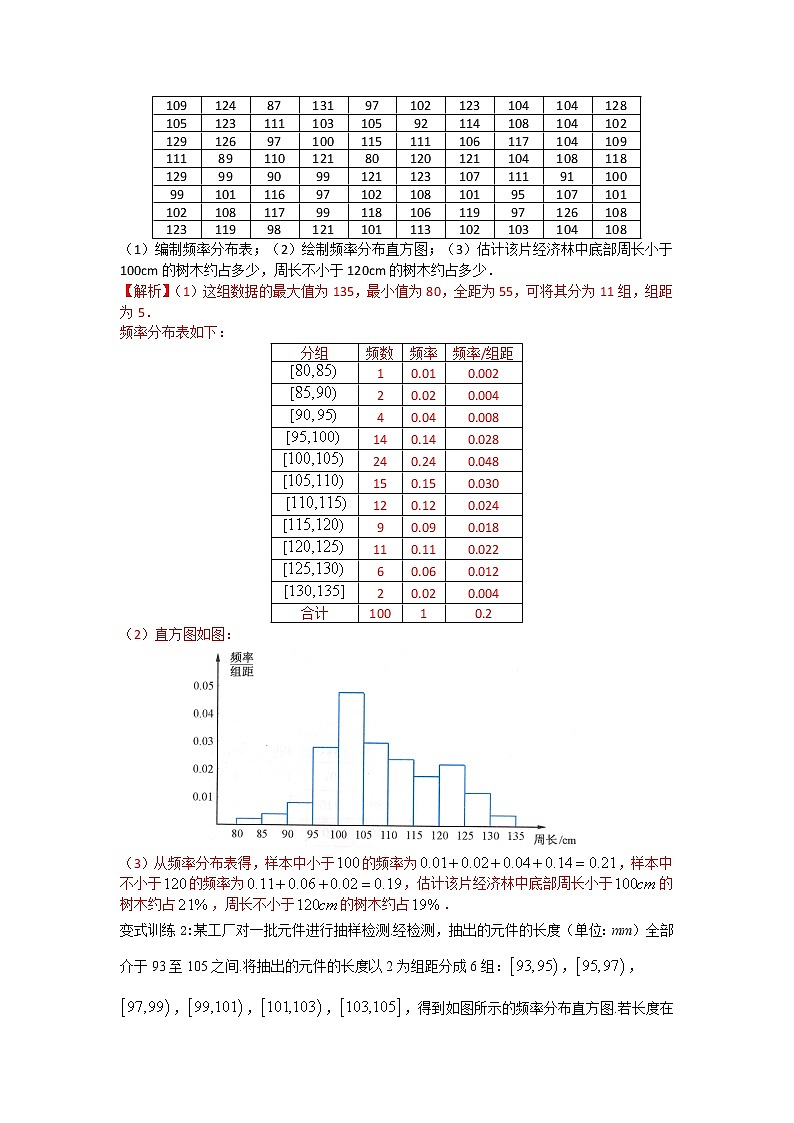
【解析】(1)这组数据的最大值为135,最小值为80,全距为55,可将其分为11组,组距为5.
频率分布表如下:
分组 | 频数 | 频率 | 频率/组距 |
1 | 0.01 | 0.002 | |
2 | 0.02 | 0.004 | |
4 | 0.04 | 0.008 | |
14 | 0.14 | 0.028 | |
24 | 0.24 | 0.048 | |
15 | 0.15 | 0.030 | |
| 12 | 0.12 | 0.024 |
9 | 0.09 | 0.018 | |
11 | 0.11 | 0.022 | |
6 | 0.06 | 0.012 | |
2 | 0.02 | 0.004 | |
合计 | 100 | 1 | 0.2 |
(2)直方图如图:
(3)从频率分布表得,样本中小于的频率为,样本中不小于的频率为,估计该片经济林中底部周长小于的树木约占,周长不小于的树木约占.
变式训练2:某工厂对一批元件进行抽样检测.经检测,抽出的元件的长度(单位:mm)全部介于93至105之间.将抽出的元件的长度以2为组距分成6组:,,,,,,得到如图所示的频率分布直方图.若长度在内的元件为合格品,根据频率分布直方图,估计这批元件的合格率是( )
A.80% B.90% C.20% D.85.5%
【答案】A
【解析】由频率分布直方图可知元件长度在内的频率为:
,
故这批元件的合格率约为80%.
故选:A.
例2.调查某校高三年级男生的身高,随机抽取40名高三男生,实测身高数据(单位:cm)如下:
171 | 163 | 163 | 166 | 166 | 168 | 168 | 160 | 168 | 165 |
171 | 169 | 167 | 169 | 151 | 168 | 170 | 168 | 160 | 174 |
165 | 168 | 174 | 159 | 167 | 156 | 157 | 164 | 169 | 180 |
176 | 157 | 162 | 161 | 158 | 164 | 163 | 163 | 167 | 161 |
(1)作出频率分布表;
(2)画出频率分布直方图.
【解析】(1)最低身高151 cm,最高身高180 cm,它们的差是,即极差为29.确定组距为4,组数为8,频率分布表如下:
分组 | 频数 | 频率 |
1 | 0.025 | |
3 | 0.075 | |
6 | 0.15 | |
9 | 0.225 | |
14 | 0.35 | |
3 | 0.075 | |
3 | 0.075 | |
1 | 0.025 | |
合计 | 40 | 1 |
(2)组距为4,结合频率分布表,可计算各组的,即可得频率分布直方图如下图所示.
变式训练:一个高中研究性学习小组对本地区2000年至2002年快餐公司发展情况进行了调查,制成了该地区快餐公司个数情况的条形图和快餐公司盒饭年销售量的平均数情况条形图(如图),根据图中提供的信息可以得出这三年中该地区每年平均销售盒饭 万盒.
【答案】 85
例3:某市四所重点中学进行高二期中联考,共有5000名学生参加,为了了解数学学科的学习情况,现从中随机地抽出若干名学生在这次测试中的数学成绩,制成如下频率分布表:
分组 | 频数 | 频率 |
① | ② | |
| 0.050 | |
| 0.200 | |
36 | 0.300 | |
| 0.275 | |
12 | ③ | |
| 0.050 | |
合计 |
| ④ |
(1)根据上面的频率分布表,推出①②③④处的数字分别为 , , , .
(2)补全上的频率分布直方图.
(3)根据题中的信息估计总体:
①成绩在120分及以上的学生人数;
②成绩在的频率.
【解析】(1)在内的人数为36人,频率为0.300.
所以抽取的人数为人
在有12人,所以对应的频率为,故③对应的数字为0.100;
根据所有频率和为1,可知④对应的数字为1.则②对应的数字为
所以①对应的人数为
故①②③④处的数字分别为3; 0.025; 0.100; 1
(2)根据频率分布表,可得频率分布直方图如下图所示:
(3)①根据频率分布表及抽取总人数为120,可得成绩在120分及以上的学生人数为
人
②根据频率分布表,将内各组的频率求和可得
变式训练:一个频率分布表(样本容量为)不小心被损坏了一部分,只记得样本中数据在上的频率为,则估计样本在、内的数据个数共有( )
A. B. C. D.
【答案】B
四、小结:
频率分布直方图绘制步骤:
频率分布直方图意义:
总体取值规律的估计:
频率分布直方图的特征:
五、作业:习题9.2.1
高中数学人教A版 (2019)必修 第二册9.2 用样本估计总体精品教案及反思: 这是一份高中数学人教A版 (2019)必修 第二册9.2 用样本估计总体精品教案及反思,共12页。
高中数学9.2 用样本估计总体第1课时教学设计: 这是一份高中数学9.2 用样本估计总体第1课时教学设计,共9页。教案主要包含了预习课本,引入新课,新知探究,典例分析,课堂小结,板书设计,作业等内容,欢迎下载使用。
高中数学人教A版 (2019)必修 第二册9.2 用样本估计总体第2课时教案: 这是一份高中数学人教A版 (2019)必修 第二册9.2 用样本估计总体第2课时教案,共7页。教案主要包含了预习课本,引入新课,新知探究,典例分析,课堂小结,板书设计,作业等内容,欢迎下载使用。













